Множество решений совокупности уравнений есть

Совокупности уравнений, неравенств, систем и т.п.

Вообще в школьных учебниках алгебры о совокупностях информации очень мало. Про совокупности упоминается лишь вскользь, да и то в старших классах. С нашей точки зрения это не очень справедливо хотя бы потому, что использование совокупностей довольно удобно при оформлении решений уравнений, неравенств и их систем. Давайте восполним этот пробел.

Ниже представлен материал, дающий общее представление о совокупностях уравнений, неравенств, систем и их всевозможных комбинаций. Здесь вы найдете определения совокупностей и их решений, принятые обозначения, а также поясняющие примеры.

Навигация по странице.

Что такое совокупность уравнений, неравенств, систем?

Сразу скажем, что если у Вас сформировано четкое представление о системах уравнений и системах неравенств, то определения совокупностей воспримутся очень легко. Прочитав их, Вы сразу почувствуете, будто уже их встречали.

Информация из учебников [1, с. 24; 2, с. 129; 3, с. 64-65] позволяет записать следующее определение совокупности уравнений:

Совокупностями уравнений называются записи, представляющие собой несколько расположенных друг под другом уравнений, которые слева объединены квадратной скобкой, и обозначающие множество всех таких решений, которые являются решениями хотя бы одного из уравнений совокупности.

Давайте проведем параллель между системами и совокупностями. Системы записывают с помощью фигурной скобки, а совокупности – с помощью квадратной, системы обозначают множество решений, которые являются решениями каждого уравнения системы, а совокупности – множество решений, которые являются решениями хотя бы одного уравнения совокупности.

Для наглядности приведем примеры совокупностей уравнений: , .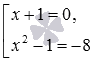

Здесь заметим, что в школе при записи совокупностей часто не используют квадратную скобку, а просто перечисляют через запятую составляющие этой совокупности. Так последняя совокупность из предыдущего абзаца может быть записана как x+y 2 +z 4 =0 , x·y·z=0 , z=5 .

Аналогично определяется и совокупность неравенств:

Совокупность неравенств – это запись, представляющая собой несколько записанных одно под другим неравенств, объединенных слева квадратной скобкой, и обозначающая множество решений, являющихся решениями хотя бы одного из неравенств совокупности.

Это определение находится в согласии с описанием совокупностей неравенств, приведенным в учебнике Мордковича [1, с. 222] .

Вот пример совокупности неравенств .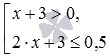

При описании совокупностей при надобности можно уточнять число составляющих их уравнений и неравенств, число переменных и вид уравнений и неравенств. К примеру, совокупность из предыдущего абзаца – это совокупность двух неравенств с одной переменной x , причем составляющие ее неравенства – целые рациональные первой степени.

Под знак совокупности можно поместить не только уравнения или неравенства по отдельности. Есть смысл рассматривать, например, совокупность уравнения и двух неравенств, неравенства и системы уравнений, совокупность двух систем неравенств и т.п. При этом главное сохранять смысл, заключающийся в совокупности, — она означает множество решений, являющихся решением хотя бы одного объекта совокупности.

Для примера приведем совокупность двух систем неравенств и совокупность такого вида .

Что называется решением совокупности?

К совокупностям непосредственно относятся их решения. Дадим определения решений совокупностей с одной переменной, а также с двумя, тремя и большим числом переменных.

Решением совокупности с одной переменной называется такое значение переменной, которое является решением хотя бы одного составляющего элемента совокупности.

Например, если речь идет о совокупности уравнений с одной переменной, то решение совокупности – это значение переменной, которое является решением хотя бы одного составляющего ее уравнения. Так x=3 – это решение совокупности неравенств , так как 3 является решением первого неравенства. А вот нуль не является решением записанной совокупности, так как это значение не является решением ни одного неравенства совокупности, действительно, 0>1 и 0 2 ≥4·0+2 – неверные числовые неравенства.

Решением совокупности с двумя, тремя и большим числом переменных называется двойка, тройка и т.д. значений переменных, являющаяся решением хотя бы одного объекта совокупности.

В качестве примера рассмотрим следующую совокупность . Пара значений (3, 0) есть решение этой совокупности, так как она является решением системы , потому что 3+0>0 и 3≥3 — верные неравенства. А пара значений x=−1 , y=2 не является решением совокупности, так как она не является решением ни уравнения x 2 +y 2 =4 , ни системы неравенств .

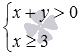
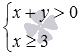
Иногда используются термины «частное решение совокупности» и «общее решение совокупности». Под частным решением совокупности понимают одно отдельно взятое решение, а общим решением называют множество всех частных решений совокупности. Но чаще говорят просто о решении совокупности, а уже из контекста черпают дополнительную информацию, о частном или об общем решении идет речь.

В заключение заметим, что из определения совокупности и ее решений следует такой вывод: решение совокупности есть объединение решений всех элементов, составляющих совокупность. А решение систем, напомним, есть пересечение решений всех ее элементов.

Продолжить изучение темы рекомендуем материалом статьи равносильные совокупности.

Множество решений совокупности уравнений есть

Решение системы уравнений. Решением системы уравнений называют значение переменной, образующие оба уравнения системы в верные числовые равенства.

Замечание. Стандартное обозначение системы: $$ \left\< \begin f_1 \left( x \right) = g_1 \left( x \right) \\ f_2 \left( x \right) = g_2 \left( x \right) \\ \end \right.$$

Пример: Решите уравнение $$ \left( \right)^2 + \left( \right)^2 = 0 $$

Решение. Слагаемые левой части данного уравнения неотрицательные, поэтому, равенство возможно, только если каждое слагаемое равно нулю: $$ \left( \right)^2 + \left( \right)^2 = 0 \Leftrightarrow \left\< \begin
\left( \right)^2 = 0 \\ \left( \right)^2 = 0 \\ \end \right. \Leftrightarrow \left\< \begin x = — 2 \\ x = 5 \\ \end \right. $$. Последние два равенства противоречат друг другу, следовательно система не имеет решения и называется несовместимой.

Совокупность уравнений. Задана совокупность двух уравнений с одной переменной, если требуется найти все такие значения переменной, при каждом из которых хотя бы одно из уравнений совокупности обращаются в верное числовое равенство.

Решение совокупности уравнений. Решением совокупности уравнений называют значение переменной, образующее хотя бы одно из уравнений совокупности в верное числовое равенство.

Пример: Решить уравнение $$ x^3 + x — 10 = 0$$

Решение. Разложим левую часть уравнения на множители $$ x^3 + x — 10 = \left( \right) + \left( <2x^2 - 4x>\right) + \left( <5x - 10>\right) = x^2 \left( \right) + 2x\left( \right) + 5\left( \right) = \left( \right)\left( \right)$$. Получим уравнение $$ \left( \right)\left( \right) = 0 \Leftrightarrow \left[ \begin
x — 2 = 0 \\ x^2 + 2x + 5 = 0 \\ \end \right. \Leftrightarrow \left[ \begin x = 2 \\ \emptyset \\ \end \right.$$. Второе уравнение совокупности не имеет решения, значит ответ x = 2

Совокупность уравнений и неравенств

Совокупность уравнений (неравенств) – это несколько неравенств или уравнений, решения которых нужно объединить.

Совокупность выглядит вот так:

Совокупности похожи на системы – в них так же присутствуют два или более неравенства (уравнения), но в отличие от системы мы ищем решение, которое подходит хотя бы одному из них (а не всем сразу).

Давайте сравним решение системы и совокупности:

Сначала в обоих случаях нужно решить каждое неравенство и нанести решения на числовую ось.

\(\begin2x>8 \; |:4\\\frac<1><2>x≤3,5 \;\;\; |\cdot 2 \end\)	\( \left[ \begin2x>8 \; \;|:4\\ \frac<1><2>x≤3,5 \;\;\; |\cdot 2\end\right.\)
\(\beginx>4\\x≤7 \end\)	\( \left[ \beginx>4\\ x≤7 \end\right.\)
Ответ: \((4;7]\)	Ответ: \((-∞;+∞)\)

То есть решение неравенств внутри системы и совокупности одинаково. Но разница появляется, когда мы начинаем искать окончательный ответ. В случае с системой мы «пересекаем» решения: т.е. ищем иксы, которые подходят и первому, и второму неравенству. А в случае с совокупностью мы «объединяем» решения, то есть находим иксы, которые подходят хотя бы одному неравенству (или обоим сразу).

Наглядно эту идею можно представить так:

решение системы решение совокупности

В первом перенесем \(-5\) в правую часть, а во втором – вынесем за скобку икс.

\( \left[ \begin\frac<3>>6\\ x(x-7) 18\\ x(x-7) квадратные с одной переменной. Решая их по отдельности (через дискриминант или по теореме Виета – неважно), находим корни:
— у первого уравнения корни: \(-3\) и \(1\);
— у второго уравнения корни: \(-3\) и \(7\).
А окончательным ответом будут они все, то есть:

Замечание: если бы мы в последнем примере решали не совокупность, а систему, то в ответ пошло бы только одно значение: \(-3\) (потому что только оно подходит обоим уравнениям сразу).