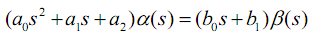Модели физических процессов с дифференциальными уравнениями

Классическая механика: о диффурах «на пальцах»

Введение

В этой статье я продолжаю тему цифровой обработки сигналов. В ней я постараюсь простым языком рассказать о концепции игровой механики (физики) с использованием подхода на основе дифференциальных уравнений. В будущем я собираюсь оценить действительно ли реализация такого подхода приведет к резкому увеличению вычислительной нагрузки. В рамках этой статьи не получится — слишком большой объем. В этой я собираюсь описать назначение коэффициентов, входящих в математическую модель динамического объекта, описать их физический смысл, т.е. их влияние на поведение динамического объекта.
Начнем пожалуй…

Физический смысл

В своей статье про Фильтр Калмана я описал что такое уравнения вида «вход-выход», передаточная функция и операторная форма записи дифференциальных уравнений (см. раздел «Основные понятия» в [2]). Примером части математической модели динамического объекта в операторной форме записи может служить следующее уравнение:
(1)
Это распространенная упрощенная модель динамических систем. Опережая напишу, что модель тела в движке «Farseer» использует урезанный аналог представленной выше модели (динамического звена второго порядка). Ниже представлено описание принятых в ней обозначений.

• а0, а1, а2 — коэффициенты инерции, демпфирования и жесткости, соответственно.
• b0, b1 — коэффициенты входного воздействия.
• s — оператор Лапласса (d/dt).
• α(s), β(s) — выходная и входная переменные, как функции оператора Лапласса.

Представленное уравнение описывает динамическую систему типа «один вход — один выход» (SISO). Ее можно использовать для описания динамики объекта по одной из его степеней свободы. Как Вам, возможно, известно, у свободного тела есть шесть степеней свободы — три поступательные (линейное движение вдоль трех осей системы координат (СК) ) и три вращательные (повороты вокруг осей СК). Таким образом, полная модель физического тела будет описываться шестью такими уравнениями (или четырьмя для 2D случая). Вы сразу можете сказать, что уже это свидетельствует о слишком высокой сложности такого подхода. Но на самом деле в Farseer, к примеру, класс тела (Body) содержит и линейные координаты тела (по сути это пара α(s) по OX и OY), и линейные скорости (пара s*α(s) по OX и OY) и параметры ориентации и угловой скорости. Эти параметры обсчитываются раздельно для каждой из осей, т.е. количество уравнений такое же — два уравнения по оси OX (линейное и угловое движение) и два для оси OY. Разница лишь в форме уравнений.
Алгоритм в движке Farseer — приближенный и упрощенный, но позволяет работать с варьируемыми квантами времени. В функцию обсчета параметров движения (Island.Solve(ref TimeStep step, ref Vector2 gravity)) передается время, прошедшее после последнего обсчета параметров. Это позволяет при недостаточной производительности компьютера держать скорость течения игрового времени примерно постоянным в ущерб плавности и реалистичности движения игровых объектов.
При построении дискретной модели на основе диференциальных уравнений мы четко завязываемся на фиксированный квант времени. Уравнения интегрируются для изначально заданной частоты дискретезации, и если с момента последнего обсчета по какой-то причине прошло времени больше, чем заданный квант (в англоязычной литературе его называют «time sample»), то мы либо должны произвести обсчет несколько раз, либо получим замедление движения объекта. Последнее я как раз и наблюдал в игре «Command Cortex» на слабой машине. Движения акторов были плавными но медленными (акторы, управляемые человеком, получают преимущество). Таким образом, нельзя говорить об исключительном преимуществе одного из этих подходов.
Теперь о том, за что отвечают коэффициенты представленного выше уравнения. Это уравнение описывает движение физического тела относительно положения равновесия при α(s) = 0. Это еще одна из причин кажущегося неудобства применения такой модели в игровой механике. При отсутствии приложенных внешних сил данная модель рано или поздно возвратит (при условии устойчивости модели) тело в положение равновесия. Представьте игровой мир, наполненный шариками, которые все время стремятся в начало координат (например, в левый верхний угол экрана). К такому поведению приводит наличие коэффициента жесткости (см. а2 выше). Представьте, что тело соединено с началом координат пружиной. Пока на тело действуют силы, пружина растянута, но стоит убрать внешнее воздействие и тело устремится к нулю. Тела в движке Farseer таким поведением не обладают. Если мы зададим коэффициент a2 равным нулю, то и в данном случае тела не будут стремиться к началу координат (см. выше я писал, что модели в Farseer по сути урезанные варианты этой модели). Ну и зачем этот коэффициент тогда нужен, спросите Вы. Если раскрыть скобки в левой части уравнения (1) и вместо слагаемого
a2*α(s)
напишем
a2*(α(s) — α0)
то через α0 мы получим возможность задать положение, к которому игровой объект будет стремиться. Величина коэффициента а2 отвечает за то, насколько быстро тело переместится в заданное положение равновесия (чем больше значение, тем выше жесткость пружины). Как такое реализовывается в Farseer я пока не выяснил, но думаю придется создать дополнительный источник воздействия.
Теперь коэффициент a1. Это коэффициент демпфирования. Чем больше значение этого коэффициента, тем быстрее гасится скорость (линейная или угловая). Аналогия из жизни — вязкие жидкости, такие как масло, мед, эпоксидная смола. Эти жидкости очень вязкие (имеют большое значение коэффициента демпфирования). Чем выше скорость движения тела в них, тем выше сопротивление этому движения. Если медленно двигать в них ложку, например, то преодолеть сопротивление большого труда не составит, а вот если ударить с размаху, то удар будет жестким.
Величина коэффициента а0 характеризует инерцию объекта. При описании линейного движения в качестве коэффициента а0 используется масса. Чем выше его значение, тем медленнее тело набирает скорость при приложении к нему внешних сил.
Теперь о коэффициентах в правой части уравнения (1). Тут нужно заметить, что данная модель расширенная на случай, когда входное воздействие определяется не только самим значением внешней силы, но и ее изменением. Для описания динамики игровых объектов это, возможно, будет излишним. Однако в промышленных системах управление встречаются и такие модели. Каков же их физический смысл? Коэффициент b1 это по сути коэффициент передачи внешней силы вовнутрь объекта. Обычно он равен еденице, т.е. сила передается как есть.
Коэффициент b0 интересен. Он играет роль форсирующего коэффициента. Представьте очень инерционный объект, к которому прикладывают силу, плавно нарастающую со временем. Если скорость нарастания и конечная величина силы будут малы, то объект очень медленно набирать скорость. Но если силу сделать большой, то после достижения внешней силой заданного значения объект не остановится в каком-то положении, а будет колебаться под действием инерции. Форсирование — это воздействие, пропорциональное скорости нарастания внешней силы. Если мы выберем его большим, то даже при малой скорости нарастания внешней силы наш объект будет достаточно быстро набирать скорость, а когда внешняя сила достигнет заданного значения, форсирование отключится. Вот такой вот хитрый этот «b0».

Динамика в картинках

Чтобы наглядно показать влияние коэффициентов дифф. уравнения на поведение динамического объекта решил построить графики переходного процесса при ступенчатом (step response) и импульсном (impulse response) входных воздействиях. Всего представлено 6 групп графиков (по одной группе для каждого коэффициента). Графики построены в пакете Octave (v. 3.4) с установленным пакетом «Signal Processing».
Итак, в качестве исходной возьмем модель вида:
=========================================
>>> w = tf([1 1],[1 1 1])

Transfer function «w» from input «u1» to output…

y1: (s + 1)/(s^2 + s + 1)

Continuous-time model.
=========================================


Код «w = tf([1 1],[1 1 1])» в символьном виде имеет вид:
>>> w = tf([b0 b1],[a0 a1 a2])
На скриншотах внизу-справа — примерное время стабилизации (коридором стабильности считаем ± 5% от заданной величины).

Попробуем поиграться с коэффициентом жесткости a2.
>>> w1 = 0.1*tf([1 1],[1 1 0.1])
y1: (s + 1)/(s^2 + s + 0.1)

>>> w2 = 10*tf([1 1],[1 1 10])
y1: (s + 1)/(s^2 + s + 10)
Примечание: пришлось подшаманить с коэффициентами усиления, чтобы результирующий коэффициент усиления был равен единице.


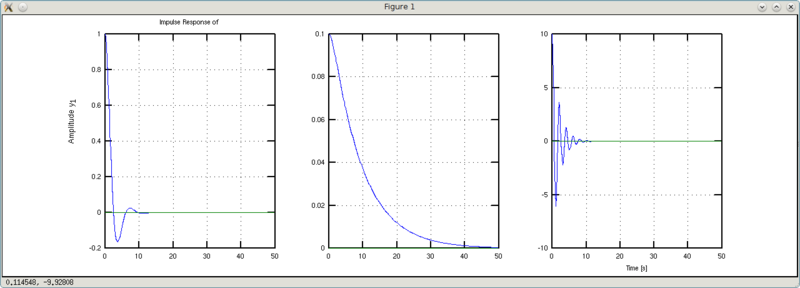
Что видно на графиках? Слева-направо представлены графики для w, w1 и w2, соответственно. Графики w1 более плавные и медленнее достигают установившегося значения. Графики w2 имеют более колебательный характер, но быстрее достигают установившегося значения. Вывод: жестче пружина — больше колебаний, но короче переходный процесс.

Попробуем поиграться с демпфированием (а1).
>>> w1 = tf([1 1],[1 0.25 1])
y1: (s + 1)/(s^2 + 0.25s + 1)

>>> w2 = tf([1 1],[1 2 1])
y1: (s + 1)/(s^2 + 2s + 1)


Сразу вывод: больше вязкость — быстрее затухают колебания.

Попробуем поиграться с инерцией (а0).
>>> w1 = tf([1 1],[0.1 1 1])
y1: (s + 1)/(0.1s^2 + s + 1)

>>> w2 = tf([1 1],[2 1 1])
y1: (s + 1)/(2s^2 + s + 1)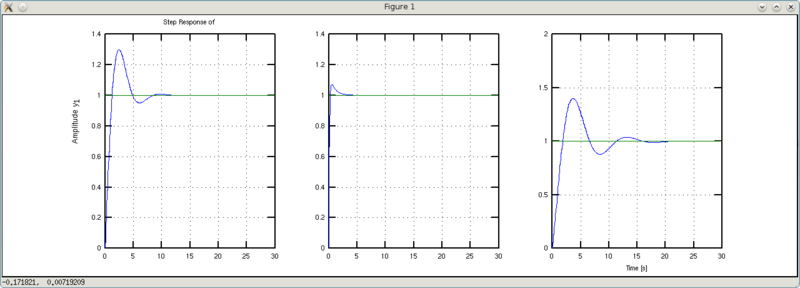


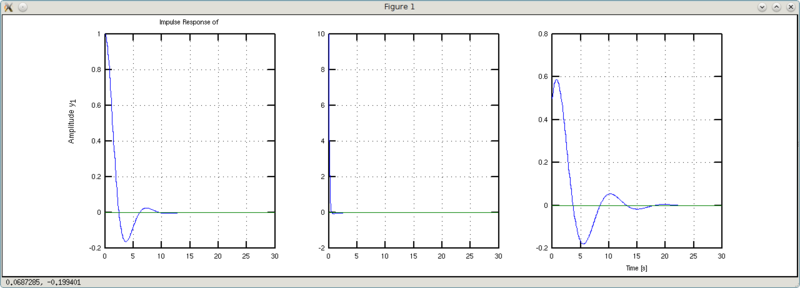
Вывод: меньше масса чугуняки — меньше болтанки и короче переходный процесс.

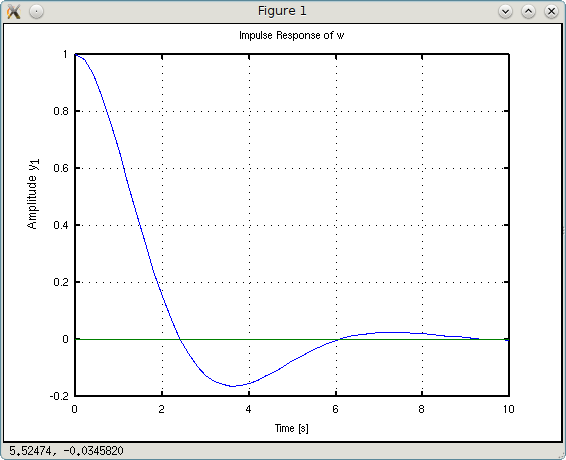
Перейдем к правой части и поиграемся с b1.
>>> w1 = 10*tf([1 0.1],[1 1 1])
y1: (10 s + 1)/(s^2 + s + 1)

>>> w2 = 0.25*tf([1 4],[1 1 1])
y1: (0.25 s + 1)/(s^2 + s + 1)


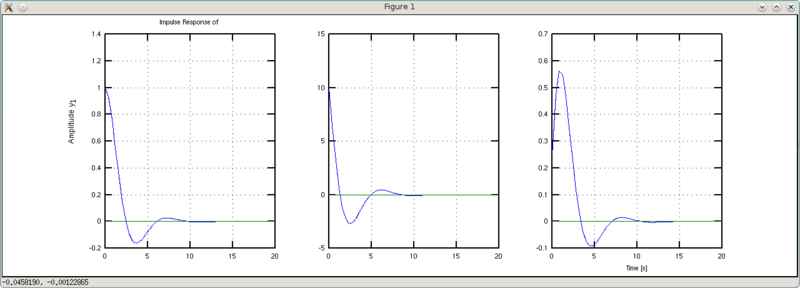
Вроде бы разница еле заметна, если смотреть на графики Step Response. Но на графиках Impulse Response хорошо виден эффект этого коэффициента. Если он равен единице, то график импульсного переходного процесса начинается с единицы (на самом деле он выходит из нуля, но не суть важно — второе значение в графике еденица). График w1 «начинается» со значения 10 (обратная величина от 0.1), а график w2 — начинается со значения 0.25 (обратное к 4). Таким образом, коэффициент b1 можно «обозвать» коэффициентом эффективности управления (входного воздействия).

И напоследок вкусненькое — игры с коэффициентом b0. Это хитрый коэффициент, потому и сравнение будет не таким как было выше. Чтобы показать его эффект придется варьровать несколько коэффициентов.
>>> w1 = tf([6 1],[1 1 1])
y1: (6 s + 1)/(s^2 + s + 1)

>>> w2 = tf([6 1],[1 3 1])
y1: (6 s + 1)/(s^2 + 3 s + 1)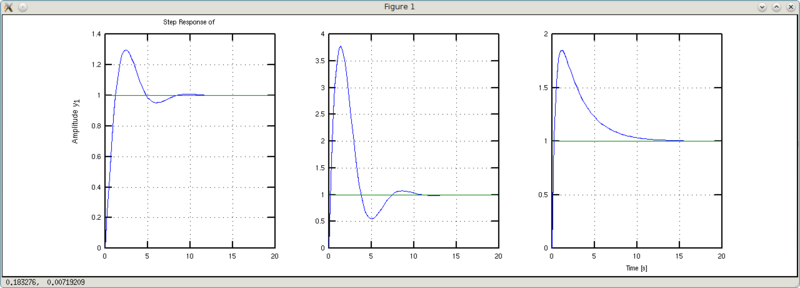


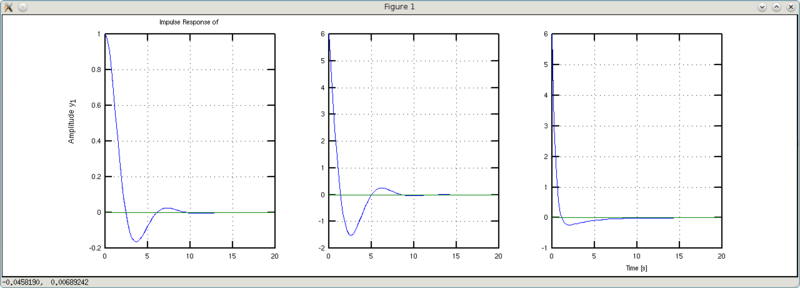
Чем отличаются друг от друга w1 и w2? У w2 в три раза больше коэффициент демпфирования. В результате получаем интересные выводы. Графики w1 и w2 раньше пересекают уровень установившегося значения чем дефолтный график. Однако график w1 сохраняет форму дефолтного с его колебательностью, а график w2 за счет увеличенного демпфирования более сглаженный. Таким образом, играясь с форсированием и демпфированием мы можем заставить даже чугунный утюг порхать по рингу как бабочка без колебаний туда-сюда.

На правах PS

В данной статье я рассматривал лишь положительные значения коэффициентов. Их положительность — необходимое условие устойчивости мат. модели. Однако можно попробовать поиграться и с отрицательными значениями. Неустойчивой системой также можно управлять. Вспомните о самолетах пятого поколения (например, наш Беркут). Обратная стреловидность крыла — это неустойчивый планер, но зато высокая маневренность. Автоматика способна скорректировать эту неустойчивость и при этом, когда нужно, закладывать крутые виражи.
Если получится, состряпаю игрушку, с которой можно будет наглядно увидеть все эти эффекты.

Модели, заданные в виде уравнений в частных производных

Ряд задач, связанных с использованием физических полей, приводит к моделям в виде дифференциальных уравнений в частных производных.

Особенностью таких задач является то, что изучаемые параметры изменяются не только во времени, но и зависят от координат x, y, z рассматриваемого пространства. Такие модели называются нестационарными. Модели, в которых параметры не зависят от времени, называются стационарными.

К таким моделям сводятся описания полей температур в элементах конструкции двигателя и полей скоростей при течении жидкости (газа). Уравнениями в частных производных описываются колебания элементов конструкции и поля напряжений, возникающих при работе этих элементов.

Линейное дифференциальное уравнение в частных производных имеет вид

.

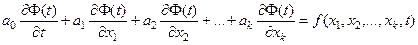
Математическая модель, описанная дифференциальными уравнениями в частных производных, должна включать в себя необходимые для решения задачи краевые условия:

1. Должна быть задана область D, ограниченная поверхностью (на плоскости – кривой) G , в которой определяется решение.

2. Должны быть заданы условия на границе G этой области.

В случае нестационарного поля эти граничные условия, так же как и сама область могут меняться во времени.

Граничные условия могут быть 1-го, 2-го и 3-го рода:

а) Граничные условия 1-го рода предусматривают задание на границе величины искомой функции:

– для стационарного поля;

– для нестационарного поля.

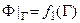
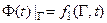
б) Граничные условия 2-го рода – предусматривают задание производной искомой функции:

– для стационарного поля;

– для нестационарного поля.

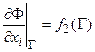
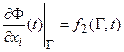
в) Граничные условия 3-го рода – предусматривают комбинации функции и ее производной:

– для стационарного поля;

– для нестационарного поля.

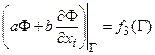
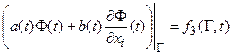
3. Для нестационарных полей должны быть заданы одно или два начальных условия, характеризующих состояние поля в начальный момент времени:

(i = 1, 2, 3).

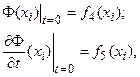
Здесь x_i – координаты пространства.

Совокупность уравнений и краевых (и начальных) условий полностью определяет модель и позволяет провести ее исследование.

Решение часто задается в виде семейств изолиний F = const (Рис. 2.11).

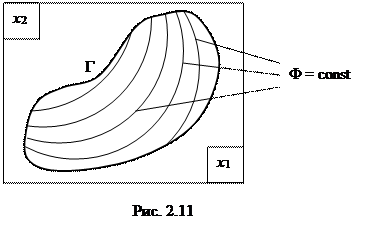В качестве примера рассмотрим хорошо изолированный металлический пруток, нагреваемый с одной стороны. С другой стороны помещен измеритель температуры (Рис. 2.12). Величина подогрева x(t) в момент времени t является входным сигналом, а измеряемая на другом конце температура y(t) – выходным сигналом.

Обозначим через x расстояние от измерителя до точки прутка. Температура в этой точке z будет описываться функцией вида

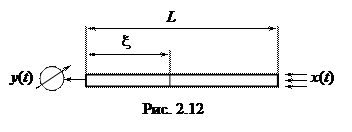
Уравнение теплопроводности для одномерного случая для определения функции z будет иметь вид:

,

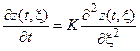
где K – коэффициент теплопроводности.

Начальным условием в данном случае является начальное распределение температуры (при t = 0) по прутку: z(0, x) = j(x).

Граничные условия определяются тремя условиями:

а) Нагрев прутка на правом конце

.

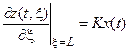
б) На левом конце подвод тепла отсутствует

.

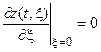
в) Показания на измерителе температур (x = 0) в момент времени t определяется следующим выражением

.

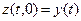
Таким образом, для вычисления температуры на расстоянии L от измерителя по формуле для y(t) необходимо проинтегрировать дифференциальное уравнение с учетом начальных и граничных условий, т.е. получить функцию z(t,x). Затем следует проградуировать измеритель температуры, т.е. определить соответствие между x(t) и y(t), задавая различные значения x(t) и вычисляя .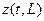

Контрольные вопросы к лекции 5

1. Где используются математические модели в виде обыкновенных дифференциальных уравнений?

2. Что должна включать в себя математическая модель в виде обыкновенных дифференциальных уравнений?

3. Какими методами осуществляется исследование моделей, заданных в виде обыкновенных дифференциальных уравнений?

4. Запишите математическую модель движения груза массой m, закрепленного на вертикальной стенке с помощью пружины жесткостью С и совершающего колебательное движение вдоль оси х в среде с вязкостью n.

5. Какой принцип используется при построении этой модели?

6. К какому типу относится эта модель?

7. Где используются математические модели в виде дифференциальных уравнений в частных производных?

8. Что является особенностью математических моделей в виде дифференциальных уравнений в частных производных?

9. Что должна включать в себя математическая модель в виде дифференциальных уравнений в частных производных?

10. Какого типа бывают граничные условия?

11. Приведите математическую модель распределения температурного поля в металлическом прутке, нагреваемом с одной стороны.

Моделирование физических задач с применением теории дифференциальных уравнений средствами MathCad и Maple

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Комитет общего и профессионального образования
Ленинградской области

Автономное образовательное учреждение
высшего профессионального образования
«Ленинградский государственный университет имени А.С.Пушкина»

Факультет математики и информатики

Кафедра информатики и вычислительной математики

КУРСОВАЯ РАБОТА

по дисциплине «Компьютерное моделирование»

Моделирование физических задач с применением теории дифференциальных уравнений средствами MathCad и Maple

студентки 4 курса,

факультета математики и информатики

(ФИО, уч степень, уч звание, долж-ть)

Оглавление

Глава 1. Теоретические сведения из теории дифференциальных уравнений и численных методов 7

§1.1. Теоретические сведения из теории дифференциальных уравнений 7

п.1. Основные сведения 7

п.2. Дифференциальное уравнение первого порядка 8

п.4. Решение дифференциальных уравнений (общее и частное решения) 9

п.5. Уравнение с разделяющимися переменными 10

§1.2. Теоретические сведения из численных методов 12

п.1. Метод Рунге-Кутта 12

п.2. Метод Эйлера 15

п.3. Погрешность методов Рунге-Кутта и Эйлера 16

Глава 2. Алгоритм построения модели и аналитическое решение построенного дифференциального уравнения 17

§2.1. Аналитическое решение построенного обыкновенного дифференциального уравнения 17

§2.2. Технология решения ОДУ в пакетах Mathcad и Maple 19

§2.3. Символьное решение в Maple 21

§2.4. Численное решение в Mathcad 24

§2.5. Сравнительная характеристика точного и численного решений 37

§2.6. Анализ результатов и выводы 39

Введение

Реальные объекты окружающего мира многообразны и сложны. Они не существуют отдельно, а находятся в некоторых отношениях, которые составляют сложную систему. Для выявления различных закономерностей в сложных системах используют моделирование.

Моделирование – это способ исследования, при котором изучение реальной системы заменяется изучением ее модели, а полученные результаты распространяются на исходные объекты.

В данной курсовой работе мы будем рассматривать математическое и компьютерное моделирование.

Математическое моделирование описывает модели на математическом языке. Выбор математической модели зависит от предметной области, в рамках которой строится и реализуется данная модель.

Далее мы будем рассматривать дифференциальную модель решения физической задачи.

Компьютерное моделирование подразумевает математическую модель, реализованную средствами какой-либо программной среды.

К основным этапам компьютерного моделирования относятся:

постановка задачи, определение объекта моделирования;

разработка концептуальной модели, выявление основных элементов системы и элементарных актов взаимодействия;

формализация, то есть переход к математической модели;

создание алгоритма и написание программы;

планирование и проведение компьютерных экспериментов;

анализ и интерпретация результатов.

В данной курсовой работе дифференциальная модель будет реализована средствами MathCad и Maple .

Система MathCAD представляет, широкие возможности для реализации различных видов дифференциальных уравнений:

встроенные функции для численного решения;

вычисление решений по итерационным формулам;

вычисление аналитических решений по готовым формулам;

запись алгоритма решения с помощью средств программирования системы MathCAD .

Для решения дифференциальных уравнений и систем дифференциальных уравнений в Maple пользователю предлагается большой набор функций, основное количество которых расположено в библиотеке DEtools . Например, для решения дифференциального уравнения первого порядка мы использовали встроенную команду dsolve .

Цели и задачи моделирования:

получение аналитического, частного и символьного решений полученного дифференциального уравнения;

построение графиков найденных решений;

анализ полученных результатов.

Цели и задачи курсовой работы:

по данным физической задачи построить дифференциальную модель;

реализовать ее средствами MathCad и Maple ;

решить задачу аналитически, символьно и численно;

сравнить полученные результаты и сделать выводы.

Постановка задачи

Условие задачи: Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости движения. Найти время движения пули через брус.

L =12 см=0.12 м – толщина бруса;

v ₀ =200 м/с — скорость, с которой пуля влетает в брус;

v ₁ =60 м/с — скорость, с которой пуля вылетает из бруса.

Разбор условия задачи и составления чертежа, поясняющего суть задачи;

Составление дифференциального уравнения рассматриваемой задачи;

Интегрирование составленного дифференциального уравнения;

Нахождение общего и частного решения задачи;

Вывод общего закона рассматриваемого процесса и числовое определение искомых величин;

Анализ ответа и проверка исходного положения задачи.

Сравнить полученный ответ с начальными данными. Оценить возможность существования полученного решения. Например, скорость движения пули через брус не может быть больше начальной скорость пули.

Найти численное решение в MathCad . Сравнить полученное численное решение с аналитическим решением, с помощью погрешности. Оценить полученные погрешности. Например, погрешность метода Рунге-Кутта не должна превосходить (-5) степень, а погрешность метода Эйлера – (-2) степени. Если погрешности в результате решения поставленной задачи получились больше указанных значений – решение неверно.

Проанализировать символьное решение в Maple , построив графики полученных решений. График символьного решения должен отличаться от графика точного решения с погрешностью, заданного метода. Т.к. на графике сложно увидеть погрешность используемых методов (например, Рунге-Кутта), то графики точного и символьного решения должны совпадать.

Глава 1. Теоретические сведения из теории дифференциальных уравнений и численных методов

§1.1. Теоретические сведения из теории дифференциальных уравнений

п.1. Основные сведения

Дифференциальные уравнения являются одним из основных математических понятий, наиболее широко применяемых при решении практических задач. Причина этого состоит в том, что при исследовании физических процессов. Решение различных прикладных задач, как правило, не удается непосредственно найти законы, связывающие величины, характеризующие исследуемые явления. Обычно легче устанавливаются зависимости между теми же величинами и их производными или дифференциалами. Соотношения такого рода и называются дифференциальными уравнениями. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную t , неизвестную функции x ( t ) этой независимой переменной и ее производные

(1)

где F – функция указанных аргументов, заданная в некоторой области их изменения.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Уравнение (1) является уравнением n -го порядка.

В теории дифференциальных уравнений изучаются и такие уравнения, которые содержат несколько независимых переменных, искомую функцию и частные производные от искомой функции по независимым переменным. Такие уравнения называются дифференциальными уравнениями с частными производными. Например, таким уравнением будет

где — искомая функция от двух независимых переменных x и y . В отличие от уравнений с частными производными, уравнения, в которых искомая функция является функцией только от одной независимой переменной, называются обыкновенными дифференциальными уравнениями.

Решения и интегральные кривые:

Всякая функция , определенная и непрерывная в интервале вместе со своими производными до порядка, равного порядку данного дифференциального уравнения, и обращающая это уравнение в тождество, справедливое при всех значениях из интервала , называется решением этого уравнения в интервале . Так, функция

будет решением уравнения в интервале , если

.

Иногда решения получают в неявном виде

или в параметрической форме

( t — параметр).

График решения дифференциального уравнения называется интегральной кривой этого уравнения. Часто ради краткости интегральную кривую называют решением.

п.2. Дифференциальное уравнение первого порядка

Рассмотрим основные понятия, относящиеся к уравнениям первого порядка общего вида. Согласно определению уравнение первого порядка имеет вид:

,

определенная и непрерывная дифференцируемая в интервале и обращающая уравнение в тождество

,

справедливое для всех значений х из интервала , называется решением уравнения в интервале .

п.3. Задача Коши

Во многих вопросах теоретического и прикладного характера требуется среди всех решений дифференциального уравнения найти решение

, (1)

удовлетворяющее условию (условию Коши)

при , (2)

где и — заданные числа, т.е. такое решение (1), в котором функция принимает заданное значение , если независимую переменную х заменить заданным значением , так что .

Геометрически это означает, что требуется найти интегральную кривую, проходящую через заданную точку .

Условие (2) называется начальным условием решения (1), а числа и — начальными данными этого решения. Обычно числа и предполагаются конечными.

п.4. Решение дифференциальных уравнений (общее и частное решения)

Дадим определение общего решения любого уравнения первого порядка в нормальной форме .

Пусть D есть некоторая область на плоскости ( х,у) , через каждую точку которой проходит одна и только одна интегральная кривая уравнения . Функция , определенная в некоторой области изменения переменных х и С и непрерывно дифференцируемая относительно х , называется общим решением уравнения в области D , если она удовлетворяет двум условиям:

1) равенство разрешимо в области D относительно произвольной постоянной С :

2) функция является решением уравнения при всех значениях произвольной постоянной С, доставляемых формулой , когда точка ( х,у ) пробегает область D .

Основное свойство общего решения состоит в возможности получения из него решения задачи Коши с начальными данными из области D .

Решение y = y ( x ) , в каждой точке которого сохраняется единственность решения задачи Коши, называется частным решением. Решение, содержащееся в формуле общего решения , т. е. получающееся из него при конкретном (допустимом) числовом значении произвольной постоянной, является частным решением.

п.5. Уравнение с разделяющимися переменными

Если дифференциальное уравнение имеет вид:

,

так что коэффициенты при dy и dy являются произведениями двух функций, из которых одна зависит только от х , а другая – только от у, то в нём можно разделить переменные. Поэтому уравнение называется уравнением с разделяющимися переменными.

§1.2. Теоретические сведения из численных методов

Решить дифференциальное уравнение численным методом — это значит для заданной последовательности аргументов и числа , не определяя функцию , найти такие значения что и

Таким образом, численные методы позволяют вместо нахождения функции получить таблицу значений этой функции для заданной последовательности аргументов. Величина называется шагом интегрирования .

п.1. Метод Рунге-Кутта

Разностной схемой задачи Коши

будем называть следующую систему линейных алгебраических уравнений относительно неизвестных у ₀ , у ₁ ,…,у _n :

Аппроксимацией дифференциальной задачи разностной схемы на решении y = y ( x ) называется замена задачи Коши задачей

Метод, предложенный К.Рунге (1905) и развитый М. Кутта (1911), позволяет строить разностные схемы различного порядка точности. Они являются наиболее употребительными в практических вычислениях.

Запишем задачу Коши следующим образом:

(1)

Идея составления разности схемы Рунге – Кутта для дифференциальной задачи (1) заключается в следующем:

Пусть значение (приближённое решение в точке ) уже найдено и требует вычислить в точке . Фиксируем положительное натуральное и вводим следующие обозначения:

где — коэффициенты, нуждающиеся в последующем определении.

Составим разностную схему:

(2)

где – коэффициенты, также нуждающиеся в определении.

Разностной схемой Рунге – Кутта порядка m будем называть разностную схему (2).

Выбор коэффициентов производится с таким расчётом, чтобы при данном значении m и любой (достаточно гладкой) функции разностная схема (2) имела бы возможно большой порядок аппроксимации.

Теперь порядок аппроксимации дифференциальной задачи разностной схемой будет определяться величиной

.

Коэффициенты выберем такими, чтобы для достаточно гладкой функции выполнялись следующие утверждения:

.

Таким образом, s – это максимальный порядок производной, равной 0 при h =0.

Воспользуемся формулой Тейлора в окрестности точки х =0 с остаточным членом в форме Коши для вычисления :

.

Таким образом, порядок аппроксимации будет равен s , т.к.

.

Запишем разностные схемы при m = 1, 2, 3 и 4 соответственно.

п.2. Метод Эйлера

Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Пусть дано дифференциальное уравнение первого порядка

(1)

с начальным условием

(2)

Требуется найти решение уравнения (1) на отрезке .

Разобьем отрезок на равных частей и получим последовательность где , а — шаг интегрирования.

Выберем -й участок и проинтегрируем уравнение (1) :

, т.е.

. (3)

Если в последнем интеграле подынтегральную функцию на участке принять постоянной и равной начальному значению в точке , то получим

.

Тогда формула (3) примет вид

. ()

Обозначив , т.е. , получим

. (4)

Продолжая этот процесс, и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной ее значению в начале участка, получим таблицу решений дифференциального уравнения на заданном отрезке .

п.3. Погрешность методов Рунге-Кутта и Эйлера

Важным этапом численного решения задачи Коши является оценка погрешности используемого метода.

Величина погрешности на сетке отрезка [ a ; b ] оценивается величиной

,

где — приближённое решение в точке — точное решение в точке , n – число точек сетки на отрезке [ a ; b ].

Часто аналитическое решение дифференциального уравнения неизвестно (или поиск его сложен), а теоретически оценить погрешность достаточно трудоемко. Поэтому на практике для оценки погрешности решения, найденного на сетке с шагом h /2 , в точке x _i  [ a ; b ] используют приближенное равенство – правило Рунге:

где p – порядок точности численного метода (для метода Эйлера р=1 , для метода Рунге-Кутта – р=4 ), — приближенное решение, вычисленное с шагом h , — приближенное решение вычисленное с шагом h /2, — точное решение в точке x _i .

Таким образом, оценка полученного результата требует проводить вычисления дважды: один раз с шагом h , другой – с шагом h /2 . за оценку погрешности решения, вычисленного с шагом h /2 , принимают величину

Погрешность метода Эйлера не должна превосходить (-2) степени. Погрешность метода Рунге-Кутта не должна превосходить (-5) степени.

Глава 2. Алгоритм построения модели и аналитическое решение построенного дифференциального уравнения

§2.1. Аналитическое решение построенного обыкновенного дифференциального уравнения

Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает, пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости. Найти время движения пули через брус.

Пусть v ₀ – скорость пули до вхождения в брус, v ₁ – скорость пули после вхождения в брус, T – время движения пули через брус.

На пулю действуют силы тяжести , и сила сопротивления , где сила сопротивления пропорциональна квадрату скорости, т.е. , где k – коэффициент пропорциональности.

Запишем второй закон Ньютона для центра масс пули:

Выберем ось x сонаправлено с вектором скорости пули.

Составим дифференциальное уравнение:

где С ₁ – произвольная константа.

По определению :

,

где С ₁ и С ₂ – произвольные константы.

То есть, искомое время T равно:

Ответ: 0,001163 секунд – время движения пули через брус.

Классифицируем данную модель по разным основаниям:

по целям моделирования – дескриптивная модель

по учету фактора времени – динамическая модель

по оператору модели – функциональная модель

по переменным и параметрам моделирования – детерминированная модель

по методам реализации – алгоритмическая модель

по характеру постановки задачи – задача анализа.

§2.2. Технология решения ОДУ в пакетах Mathcad и Maple

Для решения дифференциальных уравнений система Mathcad предоставляет широкие возможности:

встроенные функции для численного решения;

вычисление решений по итерационным формулам;

вычисление аналитических решений по готовым формулам;

использование преобразований Лапласа для решения уравнений в частных производных;

запись алгоритма решения с помощью средств программирования системы Mathcad .

Одним из преимуществ компьютерного решения дифференциальных уравнений в системе Mathcad является возможность предоставления получаемых результатов в графическом виде, что позволяет получать наиболее полную информацию о поведении решения и исследовать его.

Рассмотрим встроенные функции Mathcad, предназначенные для решения дифференциальных уравнений. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы, по крайней мере, следующие величины, необходимые для поиска решения:

набор точек, в которых нужно найти решение;

само дифференциальное уравнение, записанное в некотором специальном виде.

В данной курсовой работе будет рассмотрена одна встроенная функция, предназначенная для решения обыкновенных дифференциальных уравнений методом Рунге-Кутта:

Она предназначена для решения систем обыкновенных дифференциальных уравнений в форме Коши методом Рунге-Кутта четвёртого порядка с фиксированным шагом.

y – вектор начальных условий размерности n , где n – порядок обыкновенного дифференциального уравнения. Для обыкновенного дифференциального уравнения первого порядка вектор начальных условий вырождается в одну точку y ₀ .

x1, x2 – граничные точки интервала, на котором ищется решение дифференциального уравнения. Начальные условия, заданные в векторе y — это значение решения в точке x1 .

N – число точек (не считая начальной точки), в которых ищется приближённое решение. Число строк в матрице, возвращаемой функцией rkfixed , равно N+1 .

D(x,y) — вектор функция, состоящая из n элементов и содержащая первые производные искомых функций, т.е. правые части системы обыкновенных дифференциальных уравнений, представленных в нормальной форме (форме Коши). Для обыкновенного дифференциального уравнения первого порядка вырождается в скалярную функцию.

В результате решения получается матрица, состоящая из n – столбцов ( n – порядок ОДУ или число элементов в вектор-функции D (x, y ) , где первый столбец содержит точки, в которых ищется приближённое решение, оставшиеся столбцы содержат для обыкновенного дифференциального уравнения 1-го порядка: значения найденного приближённого решения y(x) в соответствующих точках 1-го столбца.

Для решения обыкновенного дифференциального уравнения в пакете M aple предназначена функция dsolve (deqn, var, opt) , где

deqn — одно дифференциальное уравнение n -ого порядка или система дифференциальных уравнений первого порядка (заданная в виде множества),

var — переменная или переменные, относительно которых ищется решение,

opt — необязательный аргумент, в котором можно указать вид представления решения:

При решении задачи Коши выражение deqn должно иметь структуру множества и содержать (помимо уравнения или системы уравнений) начальные условия.

§2.3. Символьное решение в Maple

Запишем условие задачи и исходные данные:

Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает, пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости. Найти время движения пули через брус.

При решении задачи используется два дифференциальных уравнения, в результате мы получаем закон изменения скорости и закон перемещения:

Запишем дифференциальное уравнение:

Найдем его общее решение:

Поставим в найденное общее решение начальное условие v 0=200 м/с:

В результате мы получили частное решение закона изменения скорости.

Продифференцируем полученное для скорости общее решение:

Подставим в полученное уравнение начальное условие х=0:

Для получения частного решения подставим в полученное уравнение значение константы С=1/200:

В результате получили частное решение закона перемещения.

Найдем численное решение для закона изменения скорости и закона перемещения:

Чтобы обратиться к переменным h и T используем функцию op [ i , e ] , которая выделяет операнд под номером i из выражения е .

Построим график полученного решения:

Закон изменения скорости:

Warning, the name changecoords has been redefined

§2.4. Численное решение в Mathcad

§2.5. Сравнительная характеристика точного и численного решений

Сравнивать полученные решения будем с помощью оценки погрешности и графическим методом.

По графикам видно, что решения методом Рунге-Кутта и методом Эйлера совпадают с точным решением.

Погрешность метода Рунге-Кутта по правилу Рунге:

Закон изменения скорости:

Погрешность метода Рунге-Кутта с точным решением:

Закон изменения скорости:

Погрешность метода Эйлера по правилу Рунге:

Закон изменения скорости:

Погрешность метода Эйлера с точным решением:

Закон изменения скорости:

Погрешности, полученные в результате решения, удовлетворяют требованиям. (Погрешность метода Эйлера не должна превосходить (-2) степени. Погрешность метода Рунге-Кутта не должна превосходить (-5) степени).

§2.6. Анализ результатов и выводы

Проанализируем решение, полученное аналитически и численными методами.

При решении дифференциального уравнения методом Рунге-Кутта мы получили наиболее точное решение. График этого решения совпадает с аналитическим решением. Метод Эйлера считается наименее точным, график его решения совпадает с точным решением при большом уменьшении шага.

Таким образом, получилось, что когда затруднён расчёт аналитического решения целесообразно использовать метод Рунге-Кутта.

Заключение

В данной курсовой работе были рассмотрены три метода решения дифференциального уравнения: аналитическое, численное (метод Рунге-Кутта и метод Эйлера). Так же в курсовой работе показано как оценивать погрешность при вычислениях численными методами. Погрешность можно оценить аналитически и графически.

При выполнении курсовой работы был сделан вывод о том, что метод Рунге-Кутта является наиболее точным.

При работе над задачей были использованы средства MathCad и Maple , т.к. они предоставляют широкие возможности для решения дифференциальных уравнений. Данные средства, благодаря встроенным функциям, позволяют получить численные решения, а так же аналитическое решение по готовым формулам.

В ходе выполнения работы мы получили как общее, так и частное решения. Результат представили не только в аналитическом, но и в графическом виде, для более наглядного представления полученных решений.

Список литературы

Алексеева Т.А. Компьютерное моделирование в пакете Mathcad (дифференциальные уравнения). Методические указания к курсовой работе. – СПб: Ленинградский государственный университет им. А.С.Пушкина, 2005. – 28с.;

Алексеева Т.А. Информационные технологии в математике. Часть I . (Система Mathcad ). Учебное пособие. 4-е изд. – СПб: Ленинградский государственный университет имени А.С.Пушкина, 2010. – 60 с.;

Алексеева Т.А., Жихарева А.А. Информационные технологии в математике. Часть II . (Пакет Maple ). Учебное пособие. – СПб: АОУ ВПО «Ленинградский государственный университет имени А.С.Пушкина», 2010. – 36с.

Бахвалов Н.С. Численные методы. – 2-е изд. – М.: Наука, 1975. – 632 с.

Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах: Учебное пособие. – М.: Изд-вл МАИ, 2000. – 380 с.