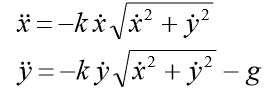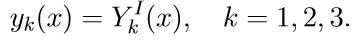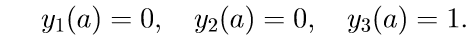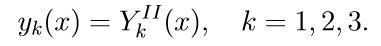Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
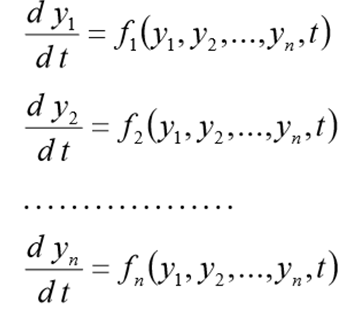
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши


по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 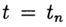

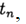


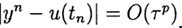


При 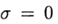
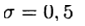
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
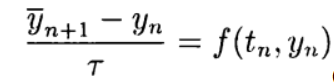
а на этапе корректора (уточнения) — схема
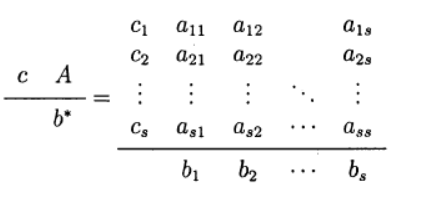
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
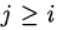

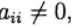
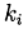
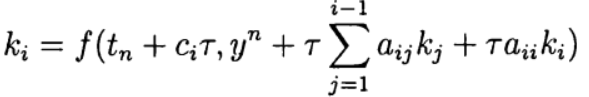
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 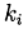
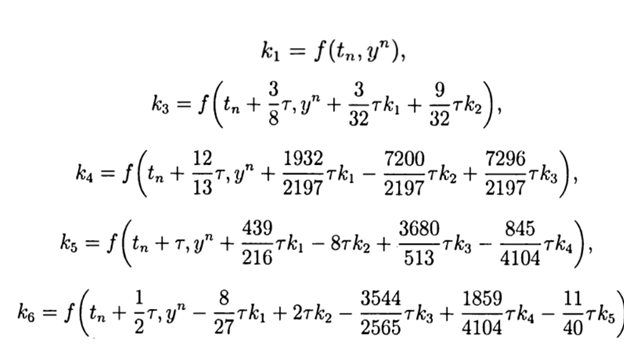
С учётом(9) общее решение имеет вид:
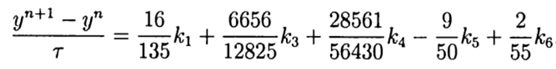
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
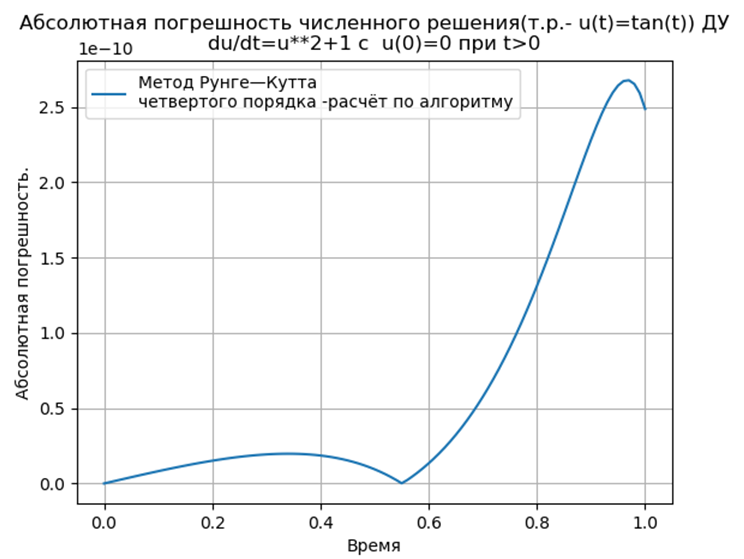
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
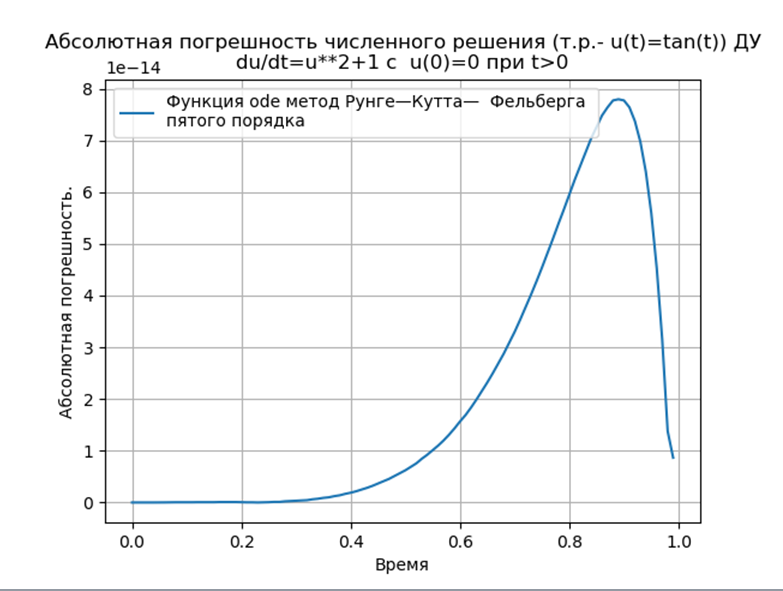
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
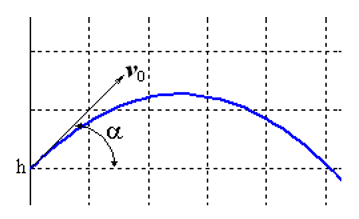
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 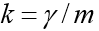
К системе следует добавить начальные условия: 

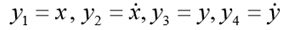
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
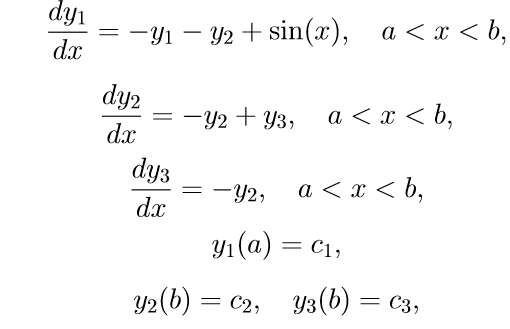
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 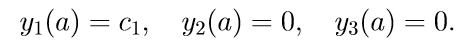
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 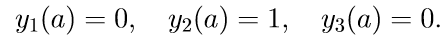
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 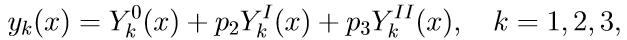
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ВВЕДЕНИЕ
Исследование поведения различных систем (сопротивления материалов, динамики, биологии, химии и других отраслей научных знаний) часто приводит к анализу и решению уравнений, включающих как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными. Дифференциальные уравнения являются фундаментом для построения научных трудов и функционально используется в производстве, что не маловажно для современной экономики и других отраслей производства.
Теория дифференциальных уравнений (ДУ) является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными.
Первая особенность – это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие – либо физические явления, исследователь прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др.
Второй особенностью теории дифференциальных уравнений является ее связь с другими разделами математики, такими, как функциональный анализ, алгебра и теория вероятностей. Теория дифференциальных уравнений и особенно теория уравнений с частными производными широко используют основные понятия, идеи и методы этих областей математики и, более того, влияют на их проблематику и характер исследований. Некоторые большие и важные разделы математики были вызваны к жизни задачами теории дифференциальных уравнений.
Таким образом, теория дифференциальных уравнений в настоящее время представляет собой исключительно богатый содержанием, быстро развивающийся раздел математики, тесно связанный с другими областями математики и с ее приложениями. Исходя из этого, цель курсовой работы состоит в изучении практических приложений дифференциальных уравнений к решению задач математической модели.
Поставленная цель достигается путем решения следующих задач:
1. Изучение ДУ первого порядка, теоретические основы дифференциальных уравнений, ДУ с разделяющимися переменными;
2. Изучение линейных ДУ второго порядка с постоянными коэффициентами.
3. Решение задач математического моделирования, химии, динамики, сопротивления материалов, радиотехники и биологии.
Объект исследования – основные понятия теории дифференциального уравнения I и II порядка.
Предмет исследования – способы реализации решения задач с помощью математического моделирования на основе дифференциальных уравнений.
1.Анализ учебной и научной литературы; 2.Изучение способов и методов реализации математических моделей; 3.Обобщение результатов.
В соответствии с целью, задачами и логикой исследования работа состоит из введения, двух глав, заключения, списка использованной литературы.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА
Дифференциальные уравнения первого порядка
Общие понятия и определения
Обыкновенным дифференциальным уравнением называется соотношение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы).
Порядком дифференциального уравнения называется наивысший порядок входящей в него производной (или дифференциала).
Дифференциальным уравнением первого порядка называется соотношение вида
где x – независимая переменная; y = y ( x ) – искомая функция; y ´( x ) = – её производная.
Если уравнение (1.1) можно записать в виде
то говорят, что оно разрешимо относительно производной.
Часто встречается дифференциальная форма записи уравнения первого порядка
которая удобна тем, что в качестве искомой функции может быть как x = x ( y ) , так и y = y ( x ).
Решением ( интегралом ) дифференциального уравнения первого порядка называется любая функция y = y ( x ), превращающая это уравнение в тождество.
График функции y = y ( x ) называется интегральной кривой.
Процесс решения дифференциального уравнения называется его интегрированием.
На самом деле в процессе интегрирования определится целый класс решений:
где C – произвольная постоянная.
Класс (1.3) называется общим решением дифференциального уравнения;
В некоторых случаях общее решение дифференциального уравнения определяется в неявном виде: Ф ( x, y, C ) = 0.
Геометрически общее решение представляет собой семейство интегральных кривых на плоскости xOy .
При каждом конкретном значении С = получают частное решение
Задача о нахождении решения дифференциального уравнения (1.2), удовлетворяющего начальному условию y () = , называется задачей Коши.
Геометрически, такая задача предполагает поиск интегральной кривой, которая проходит через заданную точку с координатами ( , ).
Решение дифференциального уравнения, которое не может быть получено из общего решения ни при одном частном значении произвольной постоянной (включая «предельные» случаи C = ±∞), называется его особым решением .
При интегрировании дифференциального уравнения надо стремиться к тому, чтобы наряду с общим решением были найдены также и особые решения.
Среди всех дифференциальных уравнений особый интерес представляют некоторые классы уравнений, для которых существуют стандартные способы аналитического решения.
1.1.2. Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение вида:
называется уравнением с разделяющимися переменными.
Разделим переменные, учитывая, что y ´( x ) = .
При этом уравнение (1.4) преобразуется к виду = f ( x ) dx .
Интегрируя, получим общее решение: ʃ
1. Характерный признак дифференциальных уравнений с разделяющимися переменными – это наличие произведений (или частных) «блоков», зависящих только от « х » или только от « у ».
2. Если обе части уравнения делим на переменную величину, то необходимо отдельно рассмотреть также случай, когда она обращается в ноль. Так, постоянные у = , для которых g() = 0 , являются, очевидно, решениями уравнения (1.4).
3. Произвольная постоянная, возникающая при интегрировании, может быть записана в виде kC или klnC , где k – любой постоянный (ненулевой) множитель. В некоторых случаях такая запись удобна для упрощения ответа.
1.1.3. Линейные уравнения первого порядка. Уравнение Бернулли
Линейным дифференциальным уравнением первого порядка называется уравнение вида
где p ( x ), q ( x ) – непрерывные (на данном интервале) функции.
Характерный признак таких уравнений – функция y и её производная содержатся в уравнении в первой степени.
Уравнение Бернулли имеет вид
Существует несколько методов решения уравнений данных видов: метод вариации произвольных постоянных, метод интегрирующего множителя, метод Бернулли.
Рассмотрим метод Бернулли . При этом решение каждого из уравнений (1.5), (1.6) будем искать в виде
По правилу дифференцирования произведения получим = v + u
(аргумент « x » в дальнейшем опускаем).
В этом случае линейное уравнение (1.6), например, записывается следующим образом
Множитель v = v ( x ) можно выбрать как некоторое решение уравнения + pv = 0 .
Тогда исходное уравнение оказывается эквивалентным уравнению с разделяющимися переменными v = q , общее решение которого есть некоторая u = u ( x , C ).
Окончательно общий интеграл линейного дифференциального уравнения примет вид
Таким образом, в процессе решения приходится дважды решать уравнения с разделяющимися переменными.
По той же схеме решается и уравнение Бернулли.
1.2. Линейные дифференциальные уравнения второго порядка
1.2.1. Основные понятия, структура общего решения
Линейным дифференциальным уравнением ( ЛДУ) второго порядка называется уравнение вида
где функции p ( x ), q ( x ), f ( x ) непрерывны на некотором интервале ( a ; b ).
Если f ( x ) ≡ 0, то уравнение (2.1) называется линейным однородным дифференциальным уравнением ( ЛОДУ ):
а в противном случае – линейным неоднородным (ЛНДУ).
Общее решение линейного однородного дифференциального уравнения имеет вид
где ( x ), ( x ) – линейно независимые решения этого уравнения (фундаментальная система решений), , – произвольные постоянные.
При этом функции ( x ) и ( x ) называются линейно независимыми в промежутке ( a ; b ), если их отношение (в этом промежутке) не является постоянной величиной. В противном случае функции называются линейно зависимыми.
Для того, чтобы частные решения уравнения (2.2) ( x ) и ( x ) были линейно независимы в промежутке ( a ; b ), необходимо и достаточно, чтобы их определитель Вронского
был отличен от нуля хотя бы в одной точке 
Общее решение н y линейного неоднородного дифференциального уравнения представляет собой сумму
где – общее решение соответствующего однородного уравнения (2.2);
– некоторое частное решение неоднородного уравнения (2.1).
Остановимся подробнее на линейных уравнениях с постоянными коэффициентами, для которых существуют стандартные алгоритмы решения.
1.2.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Если в уравнении (2.2) все коэффициенты постоянны, то оно называется линейным однородным уравнением с постоянными коэффициентами
где p , q – действительные числа.
Решение этого уравнения будем искать в виде y = . Значения параметра λ определяются как решения квадратного уравнения
которое называется характеристическим уравнением.
Чтобы получить общее решение уравнения (2.5), следует воспользоваться следующим алгоритмом :
– найти корни соответствующего характеристического уравнения
– записать фундаментальную систему решений (ФСР);
– использовать формулу (2.3) для записи .
При нахождении корней характеристического уравнения (2.6) и построении ФСР возникают следующие случаи, приведённые в табл.1.
Таким образом, решение линейного однородного дифференциального уравнения с постоянными коэффициентами сводится к вышеуказанной простой последовательности действий.
Таблица. 1. – нахождении корней характеристического уравнения
1.2.3. Системы дифференциальных уравнений
В нашей курсовой работе ограничимся рассмотрением систем двух дифференциальных уравнений. С подобными системами приходится встречаться часто в теоретической механике, сопротивлении материалов и в других приложениях математики.
Система дифференциальных уравнений первого порядка вида
где t – независимая переменная; x ( t ), y ( t ) – неизвестные функции, называется нормальной .
Пара функций x = x ( t ), y = y ( t ) является решением системы (2.7), если каждое из уравнений системы они обращают в тождество.
Класс функций вида
называется общим решением системы (2.7), если при всех значениях произвольных постоянных , , соответствующая пара функций < x , y > является решением системы.
Для системы дифференциальных уравнений (2.7) можно сформулировать задачу Коши : найти решение
удовлетворяющее начальным условиям
С точки зрения механики, решить систему – значит восстановить закон движения точки по известному вектору скорости
Иногда нормальную систему дифференциальных уравнений удаётся свести к одному уравнению второго порядка, содержащему одну неизвестную функцию. Это может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одной ( метод исключения ).
Если правые части уравнений системы (2.7) являются линейными функциями, то система называется линейной.
Ограничимся рассмотрением линейной однородной системы с постоянными коэффициентами
где a , b , p , q – некоторые числа.
Тогда система (2.13) примет вид
Пусть для определённости p ≠ 0 .
Выразим х из второго уравнения системы (2.14):
Дифференцируем второе уравнение системы (2.14) по переменной t :
Затем подставляем в него из первого уравнения системы:
В полученное равенство вместо x подставим выражение ( 2.10 ):
Соотношение (2.16) – это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, его характеристическое уравнение можно записать с помощью определителя
В соответствии с корнями , найдём фундаментальную систему решений и , а затем и общее решение уравнения (2.11):
Затем из равенства (2.15) находим функцию x ( t , , ). В результате будет получено общее решение системы (2.14).
2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ.
В различных областях человеческой деятельности возникает большое число задач, которые сводятся к решению дифференциальных уравнений. Характер этих задач и методику их решения можно схематически описать примерно так. Происходит некоторый процесс, например физический, химический, биологический. Нас интересует определенная функциональная характеристика этого процесса, например закон изменения со временем температуры или давления, массы, положения в пространстве.
Если имеется достаточно полная информация о течении этого процесса, то можно попытаться построить его математическую модель. Во многих случаях такой моделью служит дифференциальное уравнение, одним из решений которого является искомая функциональная характеристика процесса.
Дифференциальное уравнение моделирует процесс в том смысле, что оно описывает эволюцию процесса, характер происходящих с материальной системой изменений, возможные варианты этих изменений в зависимости от первоначального состояния системы.
2.1. Математическое моделирование некоторых задач химии.
Задача 1. В результате химической реакции между веществами А и B образуется вещество C . Установить зависимость количества вещества C от времени, если в момент вступления в реакцию количества веществ A и B были равны соответственно a и b . Скорость реакции пропорциональна произведению реагирующих масс.
Решение. Пусть x = x ( t ) – количество вещества C через время t после начала реакции;
– скорость образования вещества (скорость реакции). По условию
= k ( a – x ) ( b – x ), где k > 0 – коэффициент пропорциональности. Разделяем переменные и решаем уравнение:
Из начального условия x (0) = 0 находим , тогда
Выразим из этого равенства x , получим:
Если количества веществ A и B равны, т.е. a = b , то уравнение реакции примет вид:
С учётом начального условия процесс реакции описывается зависимостью x ( t ) =
2.2. Математическое моделирование некоторых задач сопротивления материалов
Задача 2. В сопротивлении материалов доказывается, что дифференциальное уравнение изогнутой оси простой балки постоянного сечения, несущей сплошную равномерно распределённую нагрузку интенсивностью q , имеет вид
где ω – прогиб балки в сечении с абсциссой x ; EI – постоянная величина, так называемая «жёсткость на изгиб сечения балки»; l – длина балки.
Найти решение этого уравнения, удовлетворяющее краевым (граничным) условиям ω(0) = 0, ω( l ) = 0, т.е. в том случае, когда на концах балки прогиб равен нулю.
Решение. Уравнение (3.7) – это уравнение второго порядка, которое допускает понижение порядка. Решим его, последовательно (дважды) интегрируя:
Первое краевое условие даёт значение = 0 , второе – значение
Искомое решение краевой задачи есть
2.3. Математическое моделирование некоторых задач динамики
Задача 3. В последовательном контуре наблюдаются свободные колебания, если отсутствует внешний источник, и конденсатор был заряжен к моменту замыкания ключа S .
После замыкания ключа S в момент времени t = 0 конденсатор разряжается через цепь с коэффициентом самоиндукции L и сопротивлением R (рис. 1). Определить напряжение на обкладках конденсатора, если в начальный момент времени
Решение. На основании законов Кирхгофа имеем:
Таким образом, получаем дифференциальное уравнение, описывающее процессы в цепи:
где α = – коэффициент затухания; – частота собственных колебаний.
Уравнение (3.2) – это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Поскольку в задании даны ещё начальные условия, то мы имеем задачу Коши.
Характеристическое уравнение, соответствующее (3.2):
Рассмотрим три случая для корней характеристического уравнения:
С учётом начальных условий решение задачи
Коши в этом случае будет иметь вид:
Если > 0 , то напряжение стремится к нулю. В контуре наблюдаются периодические, с периодом , затухающие по экспоненциальному закону колебания. Если R = 0 (т.е. отсутствует активная составляющая цепи), то напряжение на обкладках конденсатора изменяется периодически по гармоническому закону с периодом :
(гармонический колебательный процесс).
б) D = 4Решение задачи Коши в данном случае имеет
Напряжение ( t ) стремится к нулю при t → +∞ и изменяется без колебаний (затухающий апериодический процесс).
Напряжение ( t ) стремится к нулю при t → +∞ , колебаний нет, и конденсатор апериодически разряжается.
2.4. Математическое моделирование некоторых задач радиотехники
Задача 4. Найти решение системы дифференциальных уравнений
удовлетворяющее начальным условиям x (0) = y (0) = 0 , x ´(0) = μ , y ´(0) = ƞ (здесь k и g – постоянные величины).
Решение. Предложенная система описывает движение снаряда с учётом сопротивления среды. Каждое уравнение системы содержит только одну неизвестную функцию. Из первого уравнения системы имеем
Это линейное однородное уравнение второго порядка с постоянными коэффициентами. Его общее решение есть x ( t ) = + .
Для вычисления констант , используем начальные условия, в результате чего получим:
Итак, частное решение первого уравнения системы принимает вид:
Второе уравнение системы – это линейное неоднородное уравнение второго порядка с правой частью специального вида:
Общее решение второго уравнения системы:
Используя начальные условия, найдём значения , :
Тогда решение второго уравнения системы:
Окончательно получим параметрические уравнения траектории снаряда:
Если исключить параметр t из этих уравнений, то окажется, что:
Отсюда при y = 0 можно найти горизонтальную дальность стрельбы:
2.5. Математическое моделирование некоторых задач биологии
Живой организм представляет собой слишком сложную систему, чтобы его можно было рассматривать сразу во всех подробностях; поэтому исследователь всегда выбирает упрощённую точку зрения, подходящую для решения конкретно поставленной задачи. Это сознательное упрощение реальных биосистем и лежит в основе метода моделирования.
Обычно, модели, используемые в биологии, делят на три категории:
1.Биологические предметные модели, на которых изучаются общие закономерности, патологические процессы, действие различных препаратов и т. д. К этому классу моделей относят, например, лабораторных животных, изолированные органы. Культуры клеток, суспензии органелл и пр.
2.Физические ( аналоговые ) модели, т. е. физические модели, обладающие аналогичным с моделируемым объектом поведением. Например, деформации, возникающие в кости при различных нагрузках, могут быть изучены на специально подготовленном макете кости. Движение крови по крупным сосудам моделируется цепочкой резисторов, конденсаторов и индуктивных катушек.
3.Математические модели представляют собой системы математических выражений – формул, функций, уравнений и т. д., описывающих те или иные свойства изучаемого объекта, явления, процесса. При создании математической модели используют физические закономерности, выявленные при экспериментальном изучении объекта моделирования. Так, например, математическая модель кровообращения основано на законах гидродинамики.
Математическое моделирование, как метод исследования обладает рядом несомненных достоинств.
Во – первых, сам метод изложения количественных закономерностей математическим языком точен и экономичен.
Во–вторых, проверка гипотез, сформулированных на основе опытных данных, может быть осуществлена путём испытания математической модели, созданной на основе этой гипотезы. Наконец, математическая модель позволяет судить о поведении таких систем и в таких условиях, которые трудно создать в эксперименте или в клинике, изучать работу исследуемой системы целиком или работу её любой отдельной части.
Задача 5. Определить во сколько раз увеличится количество бактерий за 9 часов, если в течение 3 часов их количество изменилось от 100 да 200.
Решение. Опытным путём установлено, что скорость размножения бактерий, если для них имеется достаточный запас пищи и созданы другие необходимые внешние условия (например, отсутствие подавления бактерий другими видами), пропорциональна их количеству.
Пусть х – количество бактерий, имеющееся в данный момент, тогда скорость изменения их количества:
Так как скорость размножения бактерий пропорциональна их количеству, то существует такая k, что:
Разделяем в дифференциальном уравнении переменные:
что после потенцирования даёт:
Для нахождения С используем начальное условие: при t = 0 х = 100 . Имеем: Се˚ = 100, С = 100, и, значит , х = 100 е kt .
Коэффициент е k находим из условия: при t = 3 х = 200. Имеем:
Ответ: Количество бактерий за 9 часов увеличится в 8 раз.
Заметим, что закон, при котором скорость увеличения вещества пропорциональна наличному количеству вещества это, так называемый, закон «естественного роста».
Эта математическая модель процесса изменения количества микроорганизмов в колонии в зависимости от времени получена при очень больших предположениях (при неограниченных ресурсах питания и пространства для обитания и отсутствии межвидовой борьбы). В природе же, ни в одной из реально существующих колоний такой рост наблюдаться не может.
Ответ на вопрос, насколько закон «естественного роста» отвечает реальному процессу, даёт опытная проверка. Очевидно, что на каком-то подмножестве данные будут хорошо согласованы с моделью, а саму модель можно использовать для прогноза.
В 1845 году Ферхюлст – Перл получил уравнение, учитывающее внутривидовую борьбу микроорганизмов. В результате конкурентной борьбы внутри вида за пищу и место распространения, а так же за счёт болезней скорость роста снижается. В общем виде уменьшение прироста является некоторой новой функцией от х и Δх, которую обозначим через b ( х, Δх ) . Уменьшение количества особей в результате конкуренции тем больше, чем больше число встреч между особями, т. е. пропорционально произведению х-х т. е. х 2 . Таким образом,
Здесь ε – специфическая (врождённая) скорость размножения популяции, δ – коэффициент внутривидовой конкуренции. Разделим обе части последнего уравнения на Δt и переходя к пределу, получим
Это и есть уравнение Ферхюлста – Перла. Решением этого уравнения после математических преобразований и обозначения ε/ δ = h при t 0 = 0 и х(0) = х 0 является:
ЗАКЛЮЧЕНИЕ
Изучение большого круга задач сопротивления материалов, динамики, биологии и других отраслей научных знаний показывает, что решение многих из них сводится к математическому моделированию процессов в виде формулы, т.е. в виде функциональной зависимости.
Так, например, некоторые процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью уравнений, в которых кроме независимых переменных и неизвестных функций этих переменных, содержатся производные неизвестных функций (или их дифференциалы).
Такие уравнения называются дифференциальными.
Вот почему возможности применения дифференциальных уравнений для решения задач по дисциплинам естественно – научного цикла довольно широки.
В представленной работе:
– описаны теоретические основы дифференциальных уравнений;
– рассмотрены некоторые приёмы решения задач с помощью дифференциальных уравнений по химии, радиотехники, биологии, сопротивления материалов и динамики.
В ходе работы, возникла необходимость более полного, чем предполагалось, изучения основ моделирования реальных объектов.
Практическая ценность метода математического моделирования заключается в следующем:
– правильно составленная и всесторонне использованная математическая модель позволяет оптимизировать изучение реальной системы по времени;
– математическая модель позволяет облегчить прогнозирование хода и результатов экспериментов, проводимых в реальных системах.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Агафонов, С.А. Дифференциальные уравнения / С.А. Агафонов, А.Д. Герман, Т.В. Муратова. – МГТУ им. Н.Э. Баумана, 2004. (Сер. Математика в техническом университете; Вып. VII).
2. Берман, Г.Н. Сборник задач по курсу математического анализа: учебное пособие / Г.Н. Берман. – 22-е изд., перераб. – Спб. : Профессия, 2005.
3. Данко, П.Е. Высшая математика в упражнениях и задачах : учебное пособие для вузов. В 2 ч. Ч. 2 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 6-е изд. – М.: ООО «Издательство Оникс»; ООО Издательство «Мир и образование», 2006.
4. Каплан, И.А. Практикум по высшей математике : учебное пособие. В 2 т. Т. 2 / И.А. Каплан, В.И. Пустынников ; под общей ред. проф. В.И. Пустынникова. – 6-е изд., испр. и доп. – М. : Эксмо, 2008. (Образовательный стандарт XXI).
5. Мышкис, А.Д. Прикладная математика для инженеров. Специальные курсы / А.Д. Мышкис. – 3-е изд., доп. – М. : ФИЗМАТЛИТ, 2007.
6. Нахман, А.Д. Сборник задач по дифференциальным уравнениям и их приложениям : учебное пособие / А.Д. Нахман, С.В. Плотникова. – Тамбов : Издательство Тамб. гос. техн. ун-та, 2005.
7. Нахман, А.Д. Дифференциальные уравнения : методическое пособие / А.Д. Нахман. – Тамбов : ТОИПКРО, 2007.
8. Сборник задач по высшей математике. 2 курс / К.Н. Лунгу и др.; под ред. С.Н. Федина. – 5-е изд. – М. : Айрис-пресс, 2007.
9. Самойленко, А.М. Дифференциальные уравнения: примеры и задачи : учебное пособие / А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк. – 2-е изд., перераб. – М. : Высшая школа, 1989.
http://infourok.ru/differencialnie-uravneniya-pervogo-i-vtorogo-poryadka-kak-matematicheskie-modeli-2065750.html
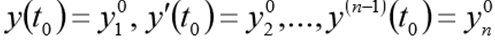


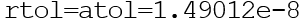
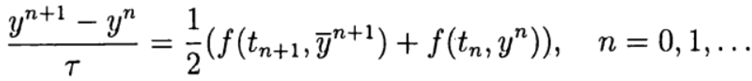
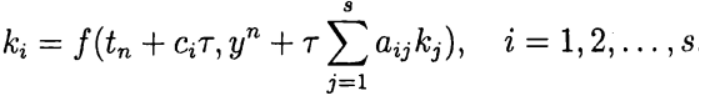
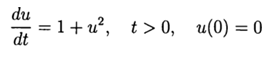 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга