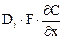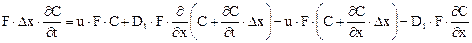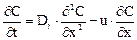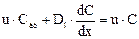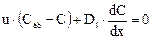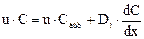Диффузионные модели.
В основе диффузионной модели лежит допущение, что структура потока описывается уравнением, аналогичным уравнению молекулярной диффузии. Параметром модели является коэффициент продольного перемешивания, называемый также коэффициентом турбулентной диффузии (или коэффициентом обратного перемешивания).
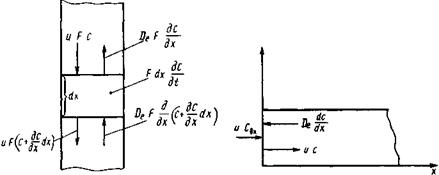
Для вывода уравнения модели составим уравнение материального баланса для элемента аппарата Δx, как показано на рис. 1. Приняты следующие обозначения: F — сечение аппарата, м 2 ; и — скорость потока, м/с; t — время, с; С — концентрация индикатора, кг/м 3 ; Dl — коэффициент продольного перемешивания, м 2 /с.
В рассматриваемый элемент поступают конвективный поток u F C и поток, вызываемый турбулентной диффузией 
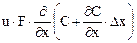
Рис. 1. К выводу уравнения диффузной ной модели
Рис. 2. Схема потоков у левого конца аппарата
В соответствии с законом сохранения массы разность между входящими и выходящими потоками должна составлять накопление вещества (индикатора) в рассматриваемом элементе. Она равна 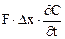
Накопление = Приход вещества — Расход вещества
Преобразуя последнее уравнение и переходя к пределу при Δх → 0, получаем
Уравнение является основным уравнением диффузионной модели.
Остановимся на начальном и граничном условиях для уравнения. Очевидно, что должны быть заданы одно начальное и два граничных условия. В качестве начального условия обычно задается профиль концентраций по аппарату в начальный момент времени:
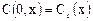
Граничные условия могут быть заданы из условия материального баланса на концах аппарата (условия по Данквертсу). Рассмотрим левый конец аппарата, в который поступает поток с некоторой средней скоростью и (рис. 2).
Рис. 3. Схема потоков у правого конца аппарата
Сумма потоков вещества, подходящих к границе х = 0, должна быть равна потоку вещества, отходящего от границы. Тогда получим
Для правого конца аппарата (рис. 3) имеем
На практике часто принимают С = СВЫХ. Сучетом этого граничное условие примет вид
Условия в таком виде называются граничными условиями по Данквертсу.
Диффузионная модель
Дата добавления: 2013-12-23 ; просмотров: 3959 ; Нарушение авторских прав
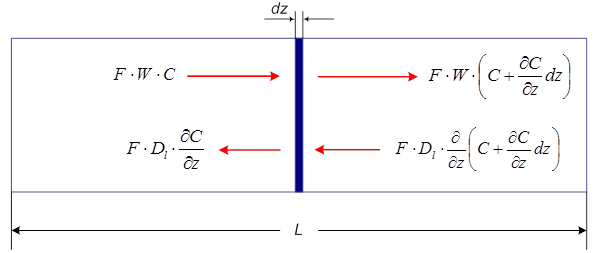
В основе диффузионной модели лежит допущение, что структура потока описывается уравнением, аналогичным уравнению молекулярной диффузии, но в отличие от коэффициента молекулярной диффузии здесь используется коэффициент продольного перемешивания или турбулентной диффузии Dl. Можно также сказать, что основой ДМ является модель ИВ, осложненная обратным перемешиванием. Параметром модели является коэффициент продольного перемешивания Dl. Принципиальная схема модели представлена на рис. 4.9.
 |
Рис. 4.9. Принципиальная схема диффузионной модели
Для получения математического описания модели составим уравнение материального баланса для элемента аппарата длиной dz. В рассматриваемый элемент поступают конвективный поток F×W×C и поток, вызываемый турбулентной диффузией 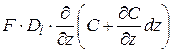
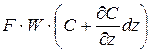
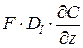
В соответствии с законом сохранения массы разность между входящим и выходящим потоками должна быть равна накоплению вещества в рассматриваемом элементе,
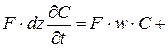 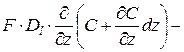 (4.22) – (4.22) –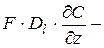 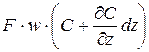 . . |
Раскрывая скобки и сокращая подобные члены, получим
 . (4.23) . (4.23) |
Данное уравнение является основным уравнением диффузии. Здесь F – площадь сечения аппарата, м 2 ; w – скорость потока, м/с; t – время, с; C – концентрация вещества, кг/м 3 ; Dl – коэффициент продольного перемешивания, м 2 /с.
На настоящий момент не существует точных аналитических методов определения коэффициента диффузии. С достаточной степенью точности его можно определить только экспериментально, например, через центральный момент второго порядка кривой отклика на импульсное возмущение и критерий Пекле,
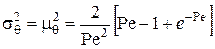 , (4.24) , (4.24) |
где 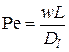
При значениях 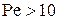
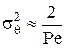 . (4.25) . (4.25) |
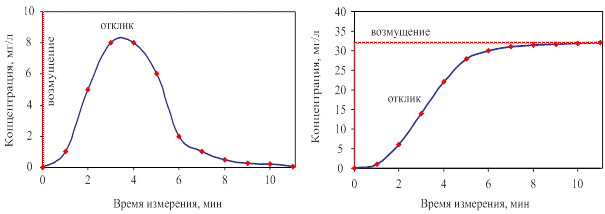
Уравнение (4.24) является основным уравнением для определения критерия Пекле по экспериментальным данным. Отклики модели на типовые возмущения представлены на рис. 4.10.
Рис. 4.10. Отклики модели на типовые возмущения
ДМ наиболее адекватно описывает структуру потока в аппаратах трубчатого и колонного типа, где наблюдается заброс вещества в сторону, противоположную направлению основного потока.
4.6. Сравнение аппаратов соответствующих
моделям ИП и ИВ
При одинаковых условиях проведения одного и того же процесса аппарат идеального вытеснения эффективнее аппарата идеального перемешивания, так как для достижения равной степени превращения в аппарате идеального перемешивания требуется большее время пребывания потока по сравнению с аппаратом идеального вытеснения. Это объясняется характером распределения концентрации реагентов по объему аппарата. Как известно, скорость протекания процесса пропорциональна его движущей силе, либо величине концентрации взаимодействующих веществ. Для массообменного и химического процесса соответственно
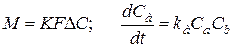 , (4.26) , (4.26) |
здесь М – количество переходящего через границу раздела фаз вещества; К – коэффициент массопередачи; F – поверхность контакта фаз; DС – движущая сила; kа – константа скорости реакции; Са, Сb – концентрация компонентов а и b соответственно.
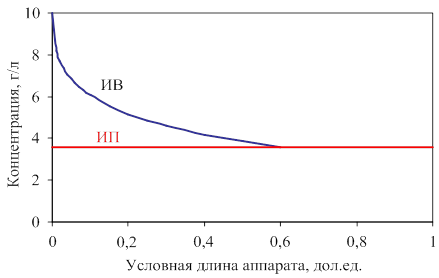
Так как для аппарата ИВ средняя движущая сила и средняя концентрация компонентов в аппарате будут всегда выше, чем в аппарате ИП, то и время пребывания в нем потока или размеры аппарата потребуются меньшие (рис. 4.11).
Рис. 4.11. Принципиальный характер изменения концентрации
реагентов по длине аппарата для моделей ИП и ИВ
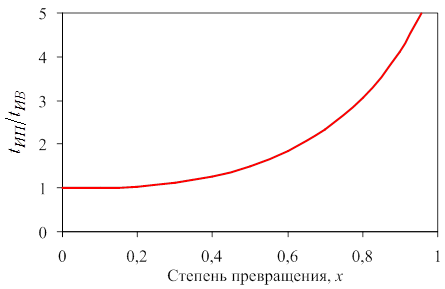
В научно-технической литературе приводится следующее примерное соотношение средних времен пребывания в аппарате ИП и ИВ, необходимое для достижения равной степени превращения x исходного вещества (рис. 4.12).
Рис. 4.12. Примерное соотношение среднего времени пребывания
в аппарате идеального перемешивания tИП и идеального вытеснения tИВ
Несмотря на низкую эффективность аппаратов ИП, благодаря простоте их изготовления и эксплуатации они нашли широкое применение в химической промышленности. Для интенсификации процессов в данном случае применяют каскад аппаратов ИП.
| | | следующая лекция ==> | |
| Ячеечная модель с рециркуляцией | | | Основные характеристики случайных величин |
Не нашли то, что искали? Google вам в помощь!
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИФФУЗИИ В ПОЛУПРОВОДНИКАХ НА ОСНОВЕ ДРОБНО-ДИФФЕРЕНЦИАЛЬНОЙ АППРОКСИМАЦИИ ПАДЕ
Литвин Н.В. 1 , Капустина Н.В. 2
1 Кандидат технических наук, доцент, 2 Старший преподаватель, Волгодонский инженерно-технический институт, Филиал Национального исследовательского ядерного университета «МИФИ»
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИФФУЗИИ В ПОЛУПРОВОДНИКАХ НА ОСНОВЕ ДРОБНО-ДИФФЕРЕНЦИАЛЬНОЙ АППРОКСИМАЦИИ ПАДЕ
Аннотация
Приведены результаты вывода математической модели диффузии в полупроводниках с использованием дробно-дифференциального исчисления. Рассмотрены основные механизмы диффузионных процессов в полупроводниках. При этом причины возникновения этого эффекта могут носить различный характер. Анализ методов моделирования диффузии позволил установить, что феноменологический подход справедлив не для всех режимов диффузии, что обусловлено перколяционным характером ее протекания. Установлено, что одним из способов моделирования диффузии является использование дробно-дифференциальных уравнений. С учетом этого в работе предложена модель диффузии на основе аппроксимации Паде с приращением изменения концентрации по времени.
Ключевые слова: фрактал, полупроводник, перколяция, дробная производная, аппроксимация Паде, потенциальная энергия.
Litvin N.V. 1 , Kapustina N.V. 2
1 PhD in Engineering, Associate Professor, 2 Senior Teacher, National Research Nuclear University (Moscow Engineering Physics Institute) (MEPhI)
MATHEMATICAL MODEL OF DIFFUSION IN SEMICONDUCTORS BASED ON PADE FREQUENCY-DIFFERENTIAL APPROXIMATION
Abstract
The article contains the results of the mathematical model derivation of diffusion in semiconductors using fractional differential calculus. The main mechanisms of diffusion processes in semiconductors are considered. At that, the causes of this effect can be of different nature. The analysis of diffusion simulation methods enabled us to establish that the phenomenological approach is valid not for all diffusion modes, which is due to the percolation nature of its course. It is established that one of the ways of modeling diffusion is the use of fractional-differential equations. With this in mind, we propose a diffusion model based on the Padé approximant with an increment in concentration change over time.
Keywords: fractal, semiconductor, percolation, fractional derivative, Padé approximant, potential energy.
Электрофизические процессы, протекающие в полупроводниках, во многом обусловлены явлениями внутреннего переноса. Помимо тока проводимости, в полупроводниках имеет место диффузионный ток. Его существование обусловлено, в отличие от тока проводимости, не разностью потенциалов, а изменением концентрации носителей. Этот ток, также как ток проводимости может быть электронным или дырочным.
В случае равномерного распределения носителей по объему полупроводника их концентрация является равновесной. Однако при наличии внешних факторов распределении концентрации носителей может стать неравномерным, что приводит к появлению электрических эффектов. Так, если часть полупроводника подвергнуть действию излучения, то в ней усилится генерация пар носителей и возникнет дополнительная концентрация носителей. Такая концентрация называется избыточной. При этом носители всегда переходят из мест с более высокой концентрацией в места с меньшей концентрацией [1,С. 24-30] ,[2,С. 40].
Перемещение атомов вещества (примеси) в решетке кристалла происходит скачками. Эти скачки происходят в трех измерениях, и суммарный поток определяется статистическим усреднением за определенный период времени.
Для описания процессов переноса и диффузии существует множество апробированных подходов. Так, для случая модели кристаллических полупроводников используется классическое уравнение диффузии. Рассмотрим его представление для одномерного случая.
Рассмотрим элементарный объем, имеющий размер Δx. Уравнение баланса переноса носителей в нем будет иметь вид [3, С. 166]:

где c(x,t) – концентрация вещества;
q(x,t) – плотность потока переноса вещества;
Δt – характерное время наблюдения.
Для плотности потока справедлив закон Фика:

В случае предельного перехода при 

В этом случае распределение фронта носителей описывается гауссовой статистикой.
Другой подход к моделированию диффузии может состоять в использовании клеточно-автоматного подхода (КА) [7, С. 10].
Клеточные автоматы (КА) относятся к классу дискретных математических моделей. Они описывают шпрокий класс реальных систем вместе с протекающими в них процессами. Содержательно клеточный автомат является бесконечной автоматной структурой, построенной следующим образом. Пусть дано n-мерное евклидово пространство. Введем его разбиение на гиперкубы с единичным ребром. При этом сохраняется свойство параллельности ребер осям координат. В каждый гиперкуб поместим один и тот же конечный автомат n входами и одним выходом. Разветвим выход автомата и соединим с входами его соседей одинаковым образом для всех гиперкубов в пространстве. Получим бесконечную однородным образом устроенную автоматную схему, которая и называется клеточным автоматом.
Последовательность состояний отдельных автоматов, содержащую состояния всех автоматов схемы, будет образовывать состояние клеточного автомата. Последовательность состояний клеточного автомата, возникающая при синхронной работе всех составляющих его конечных автоматов, называется функционированием клеточного автомата.
Одной из КА-моделей диффузии является наивная диффузия [7, С. 10-25]. Она является достаточно простой моделью. Однако при этом она на качественном уровне интерпретирует процесс как о блуждание частиц. При этом перемещение частиц стремится сделать одинаковой концентрацию вещества в пространстве. Рассматриваемый КА функционирует в асинхронном режиме. Это отвечает природе процесса диффузии. Окрестностью клетки являются её ближайшие четыре соседа. Правило функционирования заключаются в следующем. В пределах такта работы случайным образом выбирается ячейка. Она с равномерно распределенной вероятностью меняется своим значением с одной из клеток своей окрестности. Такое правило можно интерпретировать как закон сохранения массы. Случайность выбора окрестностных элементов отвечает вероятностному характеру перемещения частиц. Эта особенность отвечает в определению процесса диффузии [8, С. 1017], [9, С. 73].
Ещё одна из моделей КА-диффузии — КА-диффузия с окрестностью Марголуса [7, С. 35]. Клеточный массив разбивают на два подмножества. При этом подмножество представляет совокупность блоков, содержащих четыре клетки. Функционирование КА происходит в двухтактном синхронном режиме. Каждая итерация делится на два такта. На чётных тактах правила перехода применяются к чётным блокам, на нечётных — к нечётным. Правила перехода таковы, что выполняют сдвиг состояний в клетках блока равновероятно по часовой стрелке или против часовой стрелки. Управляя значениями вероятностей перехода и изменяя величины пространственных и временных шагов, можно моделировать процесс диффузии в широком диапазоне физических параметров [8, С. 76].
В [10, С. 112] рассматривается клеточно-автоматная модель рекомбинации. Область моделирования в ней носит дискретный характер и образует клеточное поле. Каждой клетке ставится в соответствие ее пространственное положение и состояние. Состояния клеток показывают наличие либо отсутствие в клетке частиц, участвующих в моделируемом процессе. Изменение состояний определяется правилами, описывающими поведение моделируемой системы. КА-подход позволяет непосредственно исследовать влияние пространственного распределения частиц на характер процесса рекомбинации.
Клеточные автоматы обычно используются для математического моделирования в том случае, если применение разностных методов сопряжено с затруднениями и плохо описывается дифференциальными уравнениями. Пространственно-временная дискретность и локальность действия правил КА хорошо адаптируют их реализацию на ЭВМ. Это делает их применение более рациональным по сравнению с непрерывными, и даже с рядом дискретными систем. Кроме того, клеточные автоматы не требуют выполнения операций с плавающей запятой. Они могут использовать как логические, так и целочисленные операции. Это существенно упрощает компьютерные эксперименты по исследованию КА. Особенно заметен выигрыш во времени при реализации клеточных автоматов на специализированных вычислительных машинах, обладающих большим числом параллельных процессоров – машинах клеточных автоматов.
Однако одной из специфических особенностей диффузионных процессов в полупроводниках является то, что они могут протекать при наличии перколяции [4, С. 13-17], [5, С. 20-25].
Теория перколяции является одной из моделей, позволяющей описать фазовый переход второго рода и установить момент появления глобальной связности в двухфазной системе. Выводы эти применимы к широкому классу явлений. К ним можно отнести процессы переноса в пористой среде, распространение лесных пожаров и эпидемий, описание магнитооптических эффектов в полимерных и стеклянных матрицах, содержащих неоднородности в виде металлических или полупроводниковых включений.
Альтернативным обобщением производной является дробная производная [11, С. 15-25], [11, С. 20-30]. Для вещественного показателя α, и функции f(x), такой, что выполняется правило: 

где a – вещественное число; x – текущая переменная.
Упрощением определений (4), (5) является определение Капуто, которое применимо для функций, таких, что операция дифференцирования может быть внесена под знак интеграла [12, С. 14-17]:

Наряду с (1)-(2) существует дискретное представление дробной производной, введенное А. Грюнвальдом и А.В. Летниковым как следующий предел [11, С. 17-23]:

Отметим, что формула (3) в конечном приближении наиболее широко применяется при решении дифференциальных уравнений дробного порядка . Дробное дифференцирование можно рассматривать как дифференцирование на фрактальных множествах. масштаб которых имеет степенную зависимость.
Дробно-дифференциальное представление диффузии в полупроводниках применяется достаточно давно. Так, уравнение диффузии свободных носителей с учетом захвата на локализованные состояния для времен, значительно превышающих время единичного захвата, имеет вид [13, С. 32-36], [14, С. 347]
где α – порядок дробной производной.
Уравнение (7) является обобщением уравнение классической диффузии (1). Задавая различные значения, α можно отличать различные режимы переноса носителей.
В работе предлагается обобщение (7), основанное на применении дробно-дифференциальной аппроксимации Паде временного изменения концентрации носителей. Аппроксимации Паде относятся к классу локально наилучших рациональных аппроксимаций заданного степенного ряда. Они находят разнообразные приложения в различных задачах математической физики, механики и прикладной математики.
Применим к уравнению (1) преобразование Фурье по времени. Тогда получим следующее соотношение:

где 
Перепишем множитель в левой части следующим образом

Тогда (8) примет следующей вид:

Выполним дробно-дифференциальную аппроксимацию экспоненты в (10). Для этого воспользуемся соотношением:

Удерживая члены с первым порядком, будем иметь следующую аппроксимацию
где
Из физических соображений потребуем, чтобы выполнялось соотношение 

Из вида модели (13) можно сделать вывод о том, что в процесс переноса носителей может вносить вклад скорость изменения градиента плотности потока, если под скоростью понимать дробную производную по времени. Из этого можно сделать вывод о том, что изменение плотности потока может влиять на характер релаксационных процессов при диффузии. Это, очевидно, будет способствовать более полному пониманию диффузионных процессов в дальнейшем.
Список литературы / References
- Гантмахер В.Ф. Электроны в неупорядоченных средах. – М.: ФИЗМАТЛИТ, 2013. – С. 24-40.
- Шкловский Б.И., Эфрос А.Л. Электронные свойства легированных полупроводников. Монография. – М.: Наука, Главная редакция физико-математической литературы,1979. – С.288-230
- Самарский А.А., Тихонов А.Н. Уравнения математическойфизики: Учебное пособие. – 6-е изд., испр. и доп. – М.: Изд-во МГУ, 1999 г. – С.166
- Тарасевич Ю.Ю. Перколяция: теория, приложения, алгоритмы. Учебное пособие. М.: Эдиториал УРСС, 2002. – С. 13-17
- Федер Е. Фракталы: Пер. с англ. – М.: Издательство «Мир», 1991. – С.20-25
- Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка и некоторые их приложения. Минск, Наука и техника, 1987. – 688 С.
- Тоффоли Т., Марголус Н. Машины клеточных автоматов. М.: Мир, 1991. – 280 с.
- Г. Г. Малинецкий, М. Е. Степанцов, Моделирование диффузионных процессов с помощью клеточных автоматов с окрестностью Марголуса // Ж вычисл. матем. и матем. физ., 1998. – Т. 38. – № 6. – С. 1017–1020.
- Евсеев А. А., Нечаева О. И. Клеточно-автоматное моделирование диффузионных процессов на триангуляционных сетках // ПДМ. – 2009. – № 4(6). – С. 72-83.
- Сабельфельд К.К., Киреева А.Е. дискретное стохастическое моделирование рекомбинации электронов и дырок в 2D- и ЭБ-неоднородных полупроводниках // Прикладная дискретная математика. – 2016. – № 4 (34). – С. 110-127.
- Чуриков В.А. Дополнительные главы анализа. Дробное интегрирование и дробное дифференцирование на основе d-оператора: учебное пособие / Томск: Изд-во Томского политехнического университета, 2010. – 118 с.
- Псху А.В. Уравнения в частных производных дробного порядка. — М.: Наука, 2005. – 199 с.
- Сибатов Р. Т., Учайкин В. В. Дробно-дифференциальный подход к описанию дисперсионного переноса в полупроводниках // Успехи физических наук. – – Т.179. – №10. – С. 1079-1104.
- Сибатов Р. Т., Учайкин В. В. Дробно-дифференциальная кинетика переноса заряда в неупорядоченных полупроводниках// Физика и техника полупроводников, – Т.41. – № 3. – С. 346-351.
Список литературы на английском языке / References in English
http://life-prog.ru/1_15262_diffuzionnaya-model.html
http://research-journal.org/technical/matematicheskaya-model-diffuzii-v-poluprovodnikax-na-osnove-drobno-differencialnoj-approksimacii-pade/