Модели описываемые обыкновенными дифференциальными уравнениями

В19. Модели, описываемые обыкновенными дифференциальными уравнениями. Классификация, методы решения. Методы Рунге-Кутта и прогноза и коррекции.

Любое дифференциальное уравнение или система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс. Приборы, фиксирующие то или иное физическое явление, не совершенны. Может оказаться, что малая погрешность измерения начальных данных вызывает ”ощутимые” изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление. И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математnческую модель следует признать удачной.

Обыкновенным дифференциальным уравнением n –го порядканазывается уравнение вида

F ( x , y ( x ), y ‘( x ), y »( x ), … , y ( n ) ( x )) = 0, где F — известная функция ( n + 2)-х переменных, x — независимая переменная из интервала ( a , b ), y ( x ) — неизвестная функция. Число n называется порядком уравнения.

ОДУ 1порядка

Уравнением с разделенными переменными называется дифференциальное уравнение вида f ( x ) dx + g ( y ) dy = 0 с непрерывными функциями f (х) и g ( y ).

Однородным уравнением первого порядка называется уравнение вида

Линейным дифференциальным уравнением первого порядка называется уравнение вида 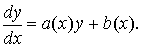Здесь a ( x ) и b ( x ) — известные, непрерывные на [ a ; b ] функции.

Уравнением Бернулли называется уравнение первого порядка вида 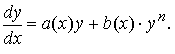Здесь a ( x ) и b ( x ) — известные, непрерывные на [ a ; b ] функции, n > 1.

Уравнение M(x, y)dx + N(x, y)dy = 0 называется уравнением в полных дифференциалах, если выражение в левой части уравнения является дифференциалом некоторой функции двух переменных F(x, y), т.е. если dF(x, y) = M(x, y)dx + N(x, y)dy. Тогда F(x, y) = C — общий интеграл уравнения. Здесь C — произвольная постоянная.

ОДУ n-ого порядкаЕсли дифференциальное уравнение F(x, y, y ‘. y ( n ) ) = 0 содержит производную неизвестной функции y = y(x) порядка n выше первого, то его называют уравнением n-го порядка и относят к уравнениям высших порядков.

Ме́тоды Ру́нге — Ку́тты— важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Метод Рунге — Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.

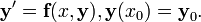
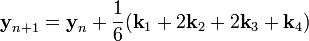
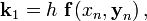
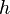
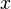
Рассмотрим задачу Коши Тогда приближенное значение в последующих точках вычисляется по итерационной формуле: Вычисление нового значения проходит в четыре стадии:

где — величина шага сетки по .

Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок (ошибка на каждом шаге порядка ).

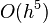
Модели, описываемые обыкновенными дифференциальными уравнениями, методы решения.

Любое дифференциальное уравнение или система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс. Приборы, фиксирующие то или иное физическое явление, не совершенны. Может оказаться, что малая погрешность измерения начальных данных вызывает ”ощутимые” изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление. И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математическую модель следует признать удачной.

Обыкновенным дифференциальным уравнением n–го порядка называется уравнение вида

F (x, y(x), y ‘(x), y »(x), … , y(n)(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Уравнением с разделенными переменными называется дифференциальное уравнение вида f(x)dx + g(y)dy = 0 с непрерывными функциями f(х) и g(y).

Однородным уравнением первого порядка называется уравнение вида

Линейным дифференциальным уравнением первого порядка называется уравнение вида Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции.

Уравнением Бернулли называется уравнение первого порядка вида Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции, n1.

Уравнение M(x, y)dx + N(x, y)dy = 0 называется уравнением в полных дифференциалах, если выражение в левой части уравнения является дифференциалом некоторой функции двух переменных F(x, y), т.е. если dF(x, y) = M(x, y)dx + N(x, y)dy. Тогда F(x, y) = C — общий интеграл уравнения. Здесь C — произвольная постоянная.

ОДУ n-ого порядка. Если дифференциальное уравнение F(x, y, y ‘,…, y(n) ) = 0 содержит производную неизвестной функции y = y(x) порядка n выше первого, то его называют уравнением n-го порядка и относят к уравнениям высших порядков.

Ме?тоды Ру?нге — Ку?тты— важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Метод Рунге — Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.

Рассмотрим задачу Коши Тогда приближенное значение в последующих точках вычисляется по итерационной формуле: Вычисление нового значения проходит в четыре стадии:

где — величина шага сетки по .

Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок (ошибка на каждом шаге порядка ).

Модели описываемые обыкновенными дифференциальными уравнениями

Простейшей моделью является обыкновенное дифференциальное уравнение первого порядка с постоянным коэффициентом [c.214]

Более общей является модель, содержащая систему линейных обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами (рис. 5.6) [c.214]

Если X(t) — случайная переменная на входе системы, a Y(t) — случайная переменная на выходе системы, обусловленная переменной X(t), то модель процесса можно описать обыкновенным дифференциальным уравнением порядка л [c.220]

Уравнение (5.17) представляет собой обыкновенное дифференциальное уравнение для / Ау(/ , 2) с независимой переменной Г2 и параметром/,. [c.221]

Более общей моделью является модель, содержащая систему линейных (по зависимым переменным) обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами, например рис. 5.10. [c.224]

Модель, содержащая одно или несколько линейных дифференциальных уравнений более высокого порядка с постоянными коэффициентами, можно преобразовать в модель, содержащую систему обыкновенных дифференциальных уравнений первого порядка. [c.226]

Кусочно-полиномиальной С.-ф. называется потому, что состоит из отдельных кусков, представляющих собой графики многочленов (ср. рис. К.8 к ст. Кусочно-линейная функция»), которые «склеены» гладким образом (если отказаться от математической терминологии — они плавно переходят друг в друга). С помощью С.-ф. удобно проводить интерполирование, т.е. восстановление недостающих элементов временного ряда. Они применяются также для построения приближенных решений обыкновенных дифференциальных уравнений. [c.339]

Комплекс моделей лесных ресурсов включает локальные, субрегиональные и региональные модели. Имеются как сосредоточенные (описываемые в терминах обыкновенных дифференциальных уравнений), так и распределенные (с уравнениями в частных производных) региональные модели. [c.174]

Задача нормирования представляет собой математическую формализацию известной природоохранной проблемы определения предельно допустимых выбросов (ПДВ), при соблюдении которых концентрации примесей в среде не превзойдут предельно допустимых (ПДК). С математической точки зрения задача нормирования ставится как задача максимизации функционала при условии, что множество достижимости управляемой динамической системы, описываемой системой обыкновенных дифференциальных уравнений, включено в заданное множество. Были предложены новые специальные методы и алгоритмы решения задачи нормирования [Модели. 1981 Планирование. 1984 Константинов, 1983 Новые. 1987]. С помощью этих методов были решены задачи нормирования гидрохимических воздействий для реки и системы рек [Планирование. 1984 Константинов, 1983] и нормирования нагрузки на лесной комплекс [Новые. 1987 Модели. 1986]. [c.177]

А относительно вектора Y2 ограничимся предположением, что характер его формирования определяется обыкновенным дифференциальным уравнением, приводимым к виду [c.22]

В термодинамике при конечном времени предполагают, что систему можно разбить на такие подсистемы, в каждой из которых в любой момент времени отклонения интенсивных переменных от их средних по объему значений пренебрежимо малы, а значит, отсутствуют связанные с этими отклонениями потоки внутри подсистем. Изменение же интенсивных переменных происходит только на границах подсистем, так что система в целом находится в неравновесном состоянии. Такое допущение позволяет использовать при описании подсистем уравнения состояния, справедливые лишь в условиях равновесия, для описания переходных процессов в системе оказывается возможным применить обыкновенные дифференциальные уравнения, а для решения экстремальных задач — методы оптимального управления объектами с сосредоточенными параметрами. [c.15]

Машина МН-14 (рис. 3.3) является типичным образцом современной аналоговой вычислительной техники высокого класса. Состав математических блоков позволяет решать обыкновенные дифференциальные уравнения до 20-го порядка, а также широкий класс других задач, к числу которых можно отнести умножение переменной на постоянный коэффициент больше или меньше единицы суммирование переменных интегрирование по времени дифференцирование воспроизведение переменных коэффициентов методом кусочно-постоянной аппроксимации перемножение двух переменных умножение или деление шести. переменных на одну общую переменную воспроизведение нелинейных функций от одной переменной методом кусочно-линейной аппроксимации воспроизведение специальных нелинейных функций воспроизведение тригонометрических функций. [c.128]

Пособие удовлетворяет требованиям новых государственных образовательных стандартов к минимуму содержания и уровню подготовки в области математики для социально-экономических направлений и специальностей и написано в соответствии с примерной программой дисциплины Математика , одобренной Научно-методическим советом по математике Министерства образования Российской Федерации. Пособие включает следующие девять разделов программы Введение в математический анализ , Основы математической логики , Дифференциальное исчисление функций одной переменной , Применение дифференциального исчисления для исследования функций и построения их графиков , Неопределенный интеграл , Определенный интеграл , Функции нескольких переменных , Обыкновенные дифференциальные уравнения , Системы обыкновенных дифференциальных уравнений . Кроме обязательного материала автор счел необходимым включить в пособие главу, посвященную разностным уравнениям, широко используемым в экономической теории. [c.9]

Все эти обозначения используются в современной математике и сейчас. Обозначение Лейбница используется преимущественно в теории обыкновенных дифференциальных уравнений (оно удобно, например, при решении так называемых уравнений с разделяющимися переменными). Обозначение Коши используют чаще в теории уравнений математической физики. Обозначением Ньютона пользуются тогда, когда хотят подчеркнуть, что роль независимой переменной играет время. [c.107]

Это обыкновенное дифференциальное уравнение второго порядка. Поскольку [c.368]

Рассмотренное дифференциальное уравнение является типичным обыкновенным дифференциальных уравнением второго порядка. [c.369]

Для решения обыкновенных дифференциальных уравнений используется команда [c.401]

Процесс выполнения такой программы заключается в вычислении по значениям величин, характеризующих динамический процесс в предыдущий момент времени, новых значений этих величин, в последующий момент времени. Другими словами, в системной динамике способ имитации основан на процессе численного интегрирования систем обыкновенных дифференциальных уравнений по схеме Эйлера, подразумевающей разбиение отрезка интегрирования (моделирования) на интервалы одинаковой длины. При этом интервал должен быть меньше любого запаздывания (задержки во времени) в моделируемой системе. Таким образом, переменный уровень аппроксимируется кусочно-линейной функцией, т.е. считается, что между соседними точками уровень изменяется по линейному закону. [c.336]

Рассматриваются системы, управляемое поведение которых описывается обыкновенными дифференциальными уравнениями. Предполагается, что начальное состояние системы, закон ее движения, целевой функционал и ограничения на фазовые координаты зависят от случайных параметров. Предварительное решение об управлении системой должно быть принято до наблюдения реализаций случайных параметров условий задачи. Невязки в ограничениях задачи, выявляющиеся после выбора предварительного решения, компенсируются коррекциями. [c.164]

Сигнал, спектральная плотность которого — дробно-рациональная функция частоты, можно представить как реакцию линейной системы на белый шум. Другими словами, такой сигнал может быть получен как решение линейного стохастического дифференциального уравнения, возмущаемого белым шумом. Случайный процесс — решение соответствующих стохастических дифференциальных уравнений — представляет собой марковский процесс или проекцию марковского процесса. Статистические характеристики марковских процессов — переходные вероятности — удовлетворяют известным дифференциальным уравнениям в частных производных А. Н. Колмогорова. Для вычисления условного математического ожидания М[т (0] гауссовского марковского процесса можно получить обыкновенное дифференциальное уравнение. Таким образом, выражение (4.8) для решения задачи (4.1) позволяет свести вычисление характеристик оптимальной в смысле задачи (4.1) фильтра- [c.315]

На макроуровне МОП — дискретные модели, элементами которых выступают объекты, рассматриваемые на микроуровне как системы. Фазовые переменные на макроуровне — это скорости, силы, потоки, давления, а сами модели выражаются обыкновенными дифференциальными уравнениями. [c.61]

Динамическая система находится в непрерывном движении, причем функция z (t) нужное число раз дифференцируема, а скачки при этом нулевые (координаты точки не меняются). Си-тема в таком случае описывается системой обыкновенных дифференциальных уравнений. [c.188]

Конечные автоматы удобны для описания любых детерминированных систем (не учитывающих случайные факторы), функционирующих в дискретном времени. Обыкновенные дифференциальные уравнения можно применить к детерминированным системам с непрерывным временем. Вероятностные автоматы дают возможность описать элементы стохастических систем с дискретным временем. Системы массового обслуживания удобны для представления стохастических систем с непрерывным временем. [c.195]

К обыкновенным дифференциальным уравнениям прибегают, как уже отмечалось, при описании элементов детерминированной динамической системы с непрерывным временем. [c.196]

Колебательные процессы в редукторе описываются системой обыкновенных дифференциальных уравнений [c.218]

Компоненты х (t) называются фазовыми координатами управляемой системы, а n-мерное евклидово пространство Е точек х — ее фазовым пространством. Эволюция состояния управляемой системы во времени определяется системой обыкновенных дифференциальных уравнений [c.24]

Задача (29 ), (30 ), (32) может быть решена тем или иным способом. В работах, развивающих этот подход, выписывается необходимое условие экстремума (предполагается при этом, что невязки х — / It] и х (0) — Х0, х (Т) — Х пренебрежимо малы в соответствии с (31), поэтому соответствующие члены просто игнорируются). Это необходимое условие, как известно, имеет форму краевой задачи для системы 2га (п — размерность х) обыкновенных дифференциальных уравнений к уравнению в вариациях (30 ) с 2га краевыми условиями добавляется еще сопряженная система [c.150]

Процессы, протекающие в системах управления, во многих случаях могут быть описаны обыкновенными дифференциальными уравнениями с определенными начальными условиями. Для одномерных нестационарных систем система управления может быть описана уравнением вида [c.305]

Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М. ИЛ, 1950. [c.469]

Пусть v (x) — поле скоростей установившегося течения. Построим линии тока — интегральные кривые системы обыкновенных дифференциальных уравнений [c.222]

Обыкновенные дифференциальные уравнения (10.2) надо дополнить условиями (см. (9.27)) [c.381]

Так, например, пусть Н = (Ht)t o является решением (обыкновенного) дифференциального уравнения [c.374]

Это дифференциальное уравнение динамики финансовой системы. Оно относится к одному из простейших типов обыкновенных дифференциальных уравнений, к так называемым линейным неоднородным уравнениям 1-го порядка. Если внешний поток нулевой, т.е. [c.392]

Математическая модель объекта на макроуровне выражается системой компонентных и топологических уравнений. Для представления свойств элементов и их связей используются обыкновенные дифференциальные уравнения. Форма их с точностью до обозначений физических величин оказывается одинако- [c.181]

В силу выпуклости существует точка и, -+ /, 6 U такая, что /