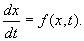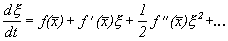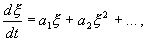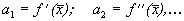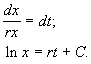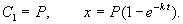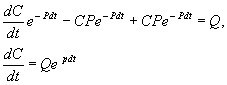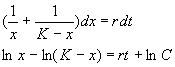Модели приводящие к одному дифференциальному уравнению

Зависимость от \( t \) обычно опускают, и пишут просто $$ \begin \dot x=kx. \label <_auto2>\end $$ Это — одно из простейших (и важнейших) дифференциальных уравнений. Неизвестной величиной в ней является не число (как в обычных алгебраических уравнениях) и не вектор (как в линейной алгебре), а функция \( x(t) \).

Рост экономики. Модель Солоу

Согласно модели Солоу, скорость прироста капитоловооруженности экономики (количества капитала в расчёте на одного трудоспособного человека) в предположении отсутствия внешней торговли, технического прогресса и роста населения, описывается формулой $$ \dot k=sf(k)-\delta k, $$ где \( k=k(t) \) — капиталовооруженность экономики в момент времени \( t \), \( s \) — норма сбережения, \( \delta \) — норма выбытия капитала.

Механическая система. Падающий шарик

Если я возьму в руку маленький тяжелый шарик, что с ним произойдёт, когда я его отпущу? Не нужно проводить этот эксперимент на практике и даже решать дифференциальное уравение, чтобы ответить: он станет падать вниз с ускорением. Это подскажет нам наша физическая интуиция. Использование интуиции и ранее накопленного опыта очень важно при решении задач, поэтому мы время от времени будем обращаться к механическим примерам.

Пусть вертикальная координата шарика (высота) в момент времени \( t \) есть \( y(t) \). Известно, что на тело, находящееся в поле тяготения земли (на не слишком большой высоте) действует сила тяжести, равная $$ F=-mg, $$ где \( m \) — масса тела, \( g \) — ускорение свободного падения (примерно равно 10 м/с 2 ), знак «-» выбран, поскольку сила тяжести действует в направлении «вниз» (против направления роста \( y \)).

С другой стороны, второй закон Ньютона гласит, что ускорение тела пропорционально действующей на него силе и обратно пропорционально массе: $$ a=F/m\quad\Leftrightarrow\quad F=ma. $$ Ускорение — это вторая производная от координаты по времени, она обозначается двумя точками. Таким образом, для шарика, имеем дифференциальное уравнение: $$ \ddot y=-g. $$

Простейшие дифференциальные уравнения

Дифференциальное уравнение общего вида

Дифференциальным уравнением называется соотношение вида $$ \dot x=f(t, x), $$ где \( x=x(t) \) — неизвестная функция, \( f(t, x) \) — известная функция двух переменных. Мы пока что будем рассматривать уравнения, в которых областью значений неизвестной функции являются вещественные числа \( \mathbb R \), но чуть позже обсудим и более сложные случаи, когда \( x \) принимает значение в многомерных пространствах.

Решением дифференциального уравнения называется дифференцируемая функция \( \newcommand<\ph><\varphi>x=\ph(t) \), такая, что при подстановке её в уравнение получается верное равенство: $$ \dot \ph(t)=f(t, \ph(t))\quad \forall t\in D(f), $$ где \( D(f) \) — область определения функции \( f \): это может быть вся числовая ось, луч, отрезок, интервал и т.д.

Рассмотрим несколько примеров.

Нулевая правая часть

Постоянная правая часть

Заметим, что в этом случае \( C \) задаёт значение функции в начальный момент времени \( t=0 \).

Правая часть, зависящая только от времени

Неопределенный интеграл по определению является семейством функций, а при записи его в виде определенного интеграла с переменным верхним пределом нужно указывать константу интегрирования явным образом.

Начальные условия. Задача Коши

Чтобы выделить среди семейства решений дифференциального уравнения одно, обычно вместе с самим дифференциальным уравнением рассматривают дополнительное соотношение, называемое начальным условием — значение решение в какой-то момент времени (не обязательно \( t=0 \)).

Когда задано дифференциальное уравнение и начальное условие, говорят, что поставлена задача Коши.

Например, можно рассмотреть такую задачу: $$ \begin \label \dot x=f(t),\quad x(5)=0 \end $$

Eё решением будет уже только одна функция: $$ \begin \label x(t)=\int_5^t f(\tau)d\tau \end $$ Действительно, любой интеграл вида \eqref является решением уравнения \eqref, а значит и функция в \eqref им является. Остаётся проверить начальное условие. При подстановке \( t=5 \) решение \( x(5)=\int_5^5 f(\tau)d\tau = 0 \), то есть начальное условие выполняется.

Модели приводящие к одному дифференциальному уравнению

МОДЕЛИ БИОЛОГИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫЕ

ОДНИМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ПЕРВОГО ПОРЯДКА

Модели, приводящие к одному дифференциальному уравнению. Понятие решения одного автономного дифференциального уравнения. Стационарное состояние (состояние равновесия). Устойчивость состояния равновесия. Методы оценки устойчивости. Решение линейного дифференциального уравнения Примеры: экспоненциальный рост, логистический рост.

Изучение математических моделей биологических систем начнем с систем первого порядка, которым соответствует одно дифференциальное уравнение первого порядка:

Если система автономная, то правая часть уравнений не зависит явно от времени и уравнение имеет вид:

(2.1)

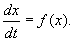
Состояние таких систем в каждый момент времени характеризуется одной единственной величиной – значением переменной x в данный момент времени t.

Рассмотрим плоскость t, x. Решениями уравнения (2.1): x( t) являются кривые на плоскости t, x , называемые интегральными кривыми (рис. 2.1)

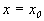
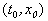
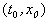
Пусть заданы начальные условия при t =0 или, иначе, пусть на плоскости t, x задана точка с координатами . Если для уравнения (2.1) выполнены условия теоремы Коши, то имеется единственное решение уравнения (2.1), удовлетворяющее этим начальным условиям, и через точку проходит одна единственная интегральная кривая x( t) .

Рис. 2.1. Интегральные кривые x ( t ); – решения уравнения f ( x ) = 0

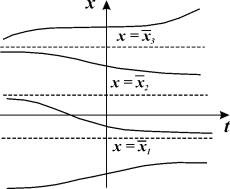
Интегральные кривые уравнения (2.1) не могут пересекаться. Решения уравнения (2.1) не могут быть периодическими, они монотонны.

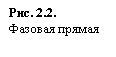
Поведение интегральных кривых на плоскости t, x можно установить, не решая в явном виде дифференциального уравнения (2.1), если известен характер движения изображающей точки на фазовой прямой.

Рассмотрим плоскость t, x , причем фазовую прямую совместим с осью x . Построим на плоскости t, x точку с абсциссой t и с ординатой, равной смещению изображающей точки по оси x в данный момент времени t. С течением времени в соответствии с уравнением (2.1) изображающая точка будет двигаться по фазовой прямой (рис. 2.2), а на плоскости t, x описывать некую кривую. Это будет интегральная кривая уравнения (2.1).

Решения одного автономного дифференциального уравнения либо уходят в бесконечность (чего не бывает в реальных системах), либо асимптотически приближаются к стационарному состоянию.

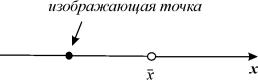
Стационарное состояние (точка покоя, особая точка, состояние равновесия)

В стационарном состоянии значения переменных в системе не меняются со временем. На языке дифференциальных уравнений это означает:

(2.2)

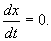
Если левая часть уравнения равна нулю, значит равна нулю и его правая часть:

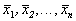
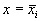
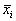
Корни алгебраического уравнения (2.3): суть стационарные состояния дифференциального уравнения (2.1). На плоскости ( t, x) прямые – асимптоты, к которым приближаются интегральные кривые. На фазовой прямой (рис. 2.2) стационарное состояние – точка, к которой стремится величина x.

Реальные биологические системы испытывают многочисленные флуктуации, переменные при малых отклонениях возвращаются к своим стационарным значениям. Поэтому при построении модели важно знать, устойчивы ли стационарные состояния модели.

Рис. 2.3. К понятию устойчивости состояния равновесия

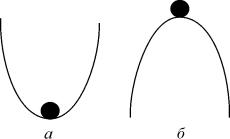
Устойчивость состояния равновесия

Каждый имеет интуитивное представление об устойчивости. На рис. 2.3. в обоих положениях (а и б) шарик находится в равновесии, т.к. сумма сил, действующих на него, равна нулю.

Попытайтесь ответить на вопрос : «Какое из этих состояний равновесия устойчиво?»

Скорее всего, Вы дали правильный ответ. Сказать, как Вы догадались? Вы дали шарику малое отклонение от состояния равновесия . В случае ( а) шарик вернулся. В случае ( б) покинул состояние равновесия навсегда.

Устойчивое состояние равновесия можно определить так: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка будет устойчивым состоянием равновесия, что соответствует устойчивому режиму функционирования системы.

Строгое математическое определение устойчивости состояния равновесия уравнения dx/dt = f( x) выглядит следующим образом :

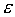
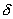
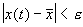
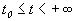
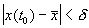
Состояние равновесия устойчиво по Ляпунову, если задав сколь угодно малое положительное , всегда можно найти такое , что

для если .

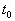
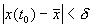
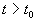
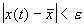
Иначе говоря, для устойчивого состояния равновесия справедливо утверждение: если в момент времени отклонение от состояния равновесия мало ( ), то в любой последующий момент времени отклонение решения системы от состояния равновесия будет также мало: .

Другими словами: c тационарное состояние называется устойчивым, если малые отклонения не выводят систему слишком далеко из окрестности этого стационарного состояния. Пример — шарик в ямке (с трением или без трения).

Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают. Пример — шарик в ямке в вязкой среде.

Стационарное состояние называется неустойчивым, если малые отклонения со временем увеличиваются. Пример: шарик на горке.

Устойчивое стационарное состояние представляет собой простейший тип аттрактора.

Аттрактором называется множество, к которому стремится изображающая точка системы с течением времени (притягивающее множество).

В нашем курсе мы рассмотрим следующие типы аттракторов:

· устойчивая точка покоя;

· предельный цикл — режим колебаний с постоянными периодом и амплитудой (начиная с размерности системы 2 );

· Области с квазистохастическим поведением траекторий в области аттрактора, например, «странный аттрактор» (начиная с размерности 3 ).

Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова). Линеаризация системы в окрестности стационарного состояния.

Метод Ляпунова приложим к широкому классу систем различной размерности, точечным системам, которые описываются обыкновенными дифференциальными уравнениями, и распределенным системам, описываемым уравнениями в частных производных, непрерывным и дискретным.

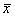
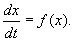
Рассмотрим метод линеаризации Ляпунова для одного автономного дифференциального уравнения первого порядка. Пусть — стационарное решение уравнения:

(2.1)

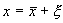
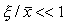
Пусть система, первоначально находившаяся в стационарном состоянии, отклонилась от него и перешла в близкую точку с координатой: , причем .

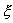
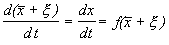
Перейдем в уравнении (2.1) от переменной x к переменной , т.е. новой переменной будет отклонение системы от стационарного состояния.

.

Учтем, что 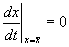по определению стационарного состояния.

Правую часть разложим в ряд Тейлора в точке :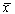

где

Отбросим члены порядка 2 и выше. Останется линейное уравнение:

(2.4)

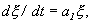
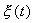
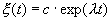
которое носит название линеаризованного уравнения или уравнения первого приближения. Интеграл этого уравнения для находится сразу:

, (2.5)

где 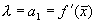, с — произвольная постоянная.

Если SYMBOL 108 \f «Symbol» \s 12 l SYMBOL 60 \f «Symbol» \s 12 0 , то при 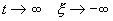и, следовательно, первоначальное отклонение SYMBOL 120 \f «Symbol» \s 12 x от состояния равновесия со временем затухает. Это означает, по определению, что состояние равновесия устойчиво.

Если же SYMBOL 108 \f «Symbol» \s 12 l SYMBOL 62 \f «Symbol» \s 12 > 0 , то при 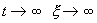, и исходное состояние равновесия неустойчиво.

Если SYMBOL 108 \f «Symbol» \s 12 l =0 , то уравнение первого приближения не может дать ответа на вопрос об устойчивости состояния равновесия системы. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора. Такие случаи мы рассмотрим в лекции 6.

Аналогичные рассуждения проводятся при рассмотрении устойчивости стационарных состояний более сложных динамических систем.

Итак, устойчивость стационарного состояния 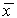уравнения dx/dt=f(x) определяется знаком производной правой части в стационарной точке.

В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).

По определению в стационарной точке правая часть уравнения (2.1) ‑ функция f(x) обращается в нуль.

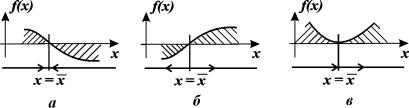
Здесь возможны три случая (рис. 2.4 а, б, в).

1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2.4 а).

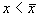
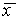
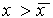
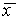
Отклоним изображающую точку системы в сторону . В этой области скорость изменения x dx/dt = f(x) положительна. Следовательно, x увеличивается, т.е. возвращается к . При скорость изменения величины x уменьшается, т.к. функция f(x) SYMBOL 60 \f «Symbol» \s 12 0. Следовательно, здесь x уменьшается и опять стремится к . Таким образом, отклонения от стационарного состояния в обе стороны затухают. Стационарное состояние устойчиво.

Рис. 2.4. Определение устойчивости стационарного состояния по графику функции f( x)

a – стационарное состояние 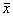устойчиво;

б, в ‑ стационарное состояние 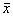неустойчиво

2. Вблизи состояния равновесия функция f ( x) меняет знак с минуса на плюс при возрастании x ( рис. 2.4 б) .

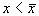
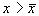
Проведите рассуждения, аналогичные случаю 1. Поместите изображающую точку в область . Теперь в область .

В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.

3. Вблизи состояния равновесия функции f(x) не меняет знак ( рис 2.4 в) .

Поскольку 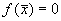, это означает, что изображающая точка, помещенная достаточно близко к состоянию равновесия с одной стороны, будет приближаться к нему, помещенная с другой стороны – удаляться.

Вопрос. Является ли состояние равновесия в случае 3 устойчивым?

Ответ. Нет. По определению устойчивости.

1. Рост колонии микроорганизмов

За время D t прирост численности равен:

где R – число родившихся и S – число умерших за время SYMBOL 68 \f «Symbol» \s 12 D t особей пропорциональные этому промежутку времени:

В дискретной форме:

.

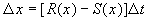
Разделив на SYMBOL 68 \f «Symbol» \s 12 D t и переходя к пределу при t SYMBOL 174 \f «Symbol» \s 12 ® 0 , получим дифференциальное уравнение

. (2.6)

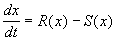
В простейшем случае, когда рождаемость и смертность пропорциональны численности:

,

(2.7)

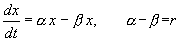
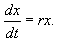
Разделим переменные и проинтегрируем:

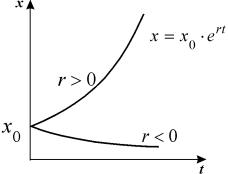
Переходя от логарифмов к значениям переменной x и определяя произвольную постоянную С из начальных условий, получим экспоненциальную форму динамики роста.

(2.8)

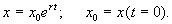
График функции (2.8) при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста представлен на рис. 2.5. Роль этой модели в развитии математической биологии и экологии мы обсудим в Лекции 3.

Рис. 2.5. Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений (2.7)

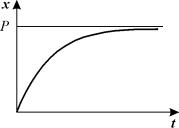
2. Вещество переходит в раствор

Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией Р и концентрацией x в данный момент времени: .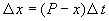

В форме дифференциального уравнения этот закон выглядит в

. (2.9)

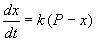
Разделим в этом уравнении переменные, и проинтегрируем:

(2.10)

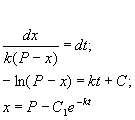
Здесь C ₁ — произвольная постоянная. Если x (0) = 0,

График этой функции представлен на рис. 2.6. – он представляет собой кривую с насыщением.

Рис. 2.6. Концентрация вещества х в зависимости от времени. График уравнения 2.9.

Какие дифференциальные уравнения можно решать аналитически?

Лишь для ограниченных классов дифференциальных уравнений разработаны аналитические методы решения. Подробно они изучаются в курсах дифференциальных уравнений. Отметим основные из них/

1. Уравнения с разделяющимися переменными решаются в интегралах. К ним относятся оба приведенные выше примера.

2. Линейные дифференциальные уравнения (не обязательно автономные).

3. Некоторые специальные виды уравнений.

Решение линейного уравнения

Линейным дифференциальным уравнением 1-го порядка называют уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

. (2.11)

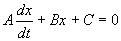
Здесь A, B, C — заданные непрерывные функции от t.

Пусть в некотором интервале изменения t A SYMBOL 185 \f «Symbol» \s 12 _ 0 . Тогда на него можно разделить все члены уравнения. При этом получим:

. (2.12)

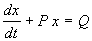
Eсли Q=0 , уравнение (2.12) называется однородным, если Q SYMBOL 185 \f «Symbol» \s 12 _ 0 – неоднородным.

Решим сначала однородное уравнение.

.

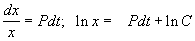
Общее решение линейного однородного уравнения имеет вид:

. (2.13)

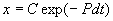
Чтобы найти решение неоднородного уравнения применим метод вариации постоянной. Будем считать С неизвестной функцией t . Подставляя правую часть выражения (2.13) в уравнение (2.12), имеем:

Теперь С находим интегрированием: 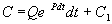. Здесь С₁ – произвольная постоянная.

Итак, общее решение линейного неоднородного уравнения первого порядка:

(2.14)

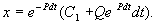
Таким образом, решение уравнения (2.12) представляет собой сумму двух слагаемых:

1) общее решение однородного уравнения (2.13) и

2) частное решение неоднородного уравнения, которое получается из общего решения, если С₁ = 0.

Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Логистическое уравнение было предложено Ферхюльстом в 1838 г. Оно имеет вид:

. (2.15)

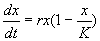
Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает, при больших – приближается к определенному пределу К .

Уравнение (2.15) можно решить аналитически. Ход решения следующий. Произведем разделение переменных:

. (2.16)

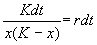
Представим левую часть в виде суммы и проинтегрируем

Переходя от логарифмов к переменным, получим:

(2.17)

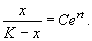
Здесь С – произвольная постоянная, которая определяется начальным значением численности x₀ :

; .

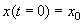
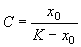
Подставим это значение С в формулу (2.17):

.

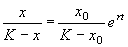
Отсюда получим решение – зависимость численности от времени:

. (2.18)

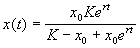
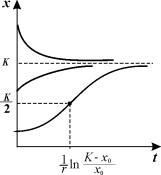
График функции (2.18) при разных начальных значениях численности популяции представлен на рис. 2.7.

Рис.2.7. Динамика численности в логистической модели 2.18

при разных начальных значениях численности

Если начальное значение х₀ К/2, кривая роста имеет точку перегиба. Если х₀ > К, численность со временем убывает.

В приведенных примерах в правой части уравнений стоят полиномы первой и второй степени. Если в правой части ‑ более сложная нелинейная функция, алгебраическое уравнение для стационарных значений может иметь несколько корней. Какое из этих решений реализуется в этом случае, будет зависеть от начальных условий.

В дальнейшем мы, как правило, не будем искать аналитическое решение для наших моделей. Для более сложных нелинейных уравнений это и невозможно. Однако важные заключения относительно свойств моделей можно сделать и на основании качественного их исследования, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний. При этом следует иметь в виду, что с помощью одного автономного дифференциального уравнения могут быть описаны только монотонные изменения переменной, и, следовательно, ни периодические, ни хаотические процессы не могут быть описаны. Для описания более сложного поведения необходимо либо переходить к системам большей размерности (2, 3 порядка и выше), либо вводить время в явном виде в правую часть уравнения. В Лекции 3 мы увидим, что дискретные уравнения и уравнения с запаздыванием могут описать и колебания, и динамический хаос.