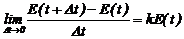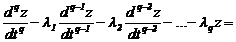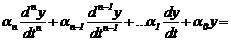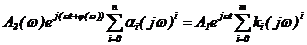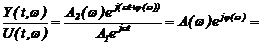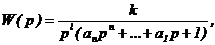Модели в форме дифференциального уравнения

Дифференциальные уравнения и математическое моделирование

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

научный руководитель канд. физ.-мат. наук, проф.

Лесосибирский педагогический институт – филиал ФГАОУ «Сибирский федеральный университет»

Для изучения объектов или процессов, протекающих в окружающем нас мире, широко используются методы математического моделирования. Математические модели являются мощным средством познания окружающего мира. При этом следует заметить, что построенная математическая модель не может отразить все многообразные и сложные черты изучаемого явления. При моделировании что-то является главным, а что-то – второстепенным, чем можно пренебречь.

Изучение большого круга задач естествознания, техники и механики, биологии, медицины и других отраслей научных знаний показывает, что решение многих из них сводится к математическому моделированию процессов в виде формулы, т. е. в виде функциональной зависимости.

Так, например, некоторые процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью уравнений, в которых кроме независимых переменных и неизвестных функций этих переменных, содержатся производные неизвестных функций (или их дифференциалы). Такие уравнения называются дифференциальными.

Вот почему возможности применения дифференциальных уравнений для решения задач по дисциплинам естественно – научного цикла довольно широки. Обыкновенные дифференциальные уравнения моделируют явления и процессы, которые описываются одной функцией или вектор-функцией одного переменного.

В математическое исследование любой задачи реального мира можно выделить три основных этапа:

1. построение математической модели явления;

2. изучение этой математической модели и получение решения соответствующей математической задачи;

3. приложение полученных результатов к практическому вопросу, из разрешения которого возникла данная математическая модель, и отыскание других вопросов, к которым она применима.

В таблице представлены основные области наук, в которых какое-либо явление или процесс можно записать в виде дифференциального уравнения.

Характеристика составления математической модели

Пример математической модели

1. Установить величины, изменяющиеся в данном явлении, и выявить физические законы, связывающие их.

2. Выбрать независимую переменную и функцию этой искомой переменной.

3. Исходя из условий задачи, определить начальные или краевые условия.

4. Выразить все фигурирующие в условии задачи величины через независимую переменную, искомую функцию и производные этой функции.

5. Исходя из условий задачи и физического закона, которому подчиняется данное явление, составить дифференциальное уравнение.

6. Найти общее решение или общий интеграл дифференциального уравнения.

7. По начальным или краевым условиям найти частное решение.

8. Исследовать полученное решение.

А) Первый закон Ньютона:

Б) Уравнение показательного роста и показательного убывания:

где – некоторая константа.

В) Уравнение гармонического колебания:

где – положительная постоянная.

где – радиус Земли, – расстояние между центрами метеороида и Земли, – ускорение свободного падения.

1. Сделать чертёж и ввести обозначения;

2. Отделить условия. Имеющие место в произвольной точке искомой линии, от условий, выполняющихся лишь в отдельных точках;

3. Выразить все упомянутые в задаче величины через координаты произвольной точки и через значение производной в этой точке, учитывая геометрический смысл производной;

4. По условию задачи составить дифференциальное уравнение;

5. Найти общее решение этого уравнения и получить из него с помощью начальных условий уравнение искомой линии.

Формула зеркала, собирающего все параллельные лучи в одну точку:

При создании математической модели используют физические закономерности, выявленные при экспериментальном изучении объекта моделирования. Так, например, математическая модель кровообращения основано на законах гидродинамики.

Модель хищник – жертва:

где – положительные константы, – число хищников, – число жертв.

Сущность химических реакций сводится к разрыву связей в исходных веществах и возникновению новых связей в продуктах реакции. При этом общее число атомов каждого элемента до и после реакции остаётся постоянным.

Закон действующих масс:

где – концентрации веществ

– коэффициент пропорциональности.

Базовая математическая модель в области финансов формулируется в терминах стохастических процессов, приводящих, таким образом, к стохастическим дифференциальным уравнениям. Время и недостоверность являются главными элементами моделирования финансового поведения экономических агентов.

Модель фондового (биржевого) ценообразования:

где и – постоянные коэффициенты, связанные с характеристиками модели.

Компартментальное моделирование распространено в медицине и биологии. Согласно определению американского фармаколога и биохимика Шеппарда компартмент — это некоторое количество вещества, выделяемое в биологической системе и обладающее свойством единства, поэтому в процессах транспорта и химических преобразований его можно рассматривать как целое. Например, в качестве особых компартментов рассматривают весь кислород в легких, всю углекислоту в венозной крови, количество введенного препарата в межклеточной жидкости, запас гликогена в печени и т. п. Модели, в которых исследуемая система представляется в виде совокупности компартментов, потоков вещества между ними, а также источников и стоков всех веществ, называются компартментальными.

Модель роста опухоли:

где – концентрация опухолевых клеток, – внеклеточная матрица (например, IV тип коллагена).

В заключение отметим, что математическая модель является основой математически оформленной теории того или иного явления, а аппарат дифференциальных уравнений нашел большое применение в математическом моделировании.
Результативность математического моделирования подтверждена всей человеческой практикой, это сильное средство научного исследования, которое используют в каждой конкретной области науки.

Математическая модель в виде обыкновенных дифференциальных уравнений

2.5. Математическая модель в виде обыкновенных дифференциальных уравнений

Математическая модель в виде одного или нескольких обыкновенных дифференциальных уравнений (ОДУ) широко используются при изучении переходных процессов в системах автоматического регулирования (САР), при описании баллистики летательных аппаратов, а также при описании процессов движения (потоки, частицы, механические элементы).

В простейшем случае модель может иметь вид линейного дифференциального уравнения n-го порядка:

или системы дифференциальных уравнений 1-го порядка

Часто встречаются смешанные задачи, а также нелинейные ОДУ.

Модель, заданная в виде дифференциальных уравнений, должна включать в себя необходимый набор начальных условий:

Рекомендуемые файлы

Исследование моделей, заданных в виде обыкновенных дифференциальных уравнений, осуществляется аналитическими и численными методами. Наиболее полными являются аналитические решения, обеспечивающие всесторонний анализ полученных результатов. Но такие решения получены лишь для ограниченного числа дифференциальных уравнений. Численные методы решения позволяют найти лишь конкретные значения изучаемой функции при заданной комбинации исходных данных. Для анализа модели можно использовать некоторую совокупность решений. Однако, очевидно, что результаты анализа в этом случае могут зависеть от выбора этой совокупности.

Возмущающая сила, вызывающая колебания, зависит от времени f(t). Наряду с возмущающей силой f(t) на груз действует сила инерции , сила вязкого трения , усилие пружины . Все эти силы тормозят движение груза.

Согласно принципу Даламбера сумма всех сил, действующих на груз должна равняться нулю:

. (2.18)

Начальные условия характеризуют начальное положение и начальную скорость груза:

x(0) = x₀; . (2.19)

Уравнение (2.18) совместно с начальными условиями (2.19) представляет собой математическую модель рассматриваемой механической системы.

2.6. Модели, заданные в виде уравнений в частных производных

Ряд задач, связанных с использованием физических полей, приводит к моделям в виде дифференциальных уравнений в частных производных.

Особенностью таких задач является то, что изучаемые параметры изменяются не только во времени, но и зависят от координат x, y, z рассматриваемого пространства. Такие модели называются нестационарными. Модели, в которых параметры не зависят от времени, называются стационарными.

К таким моделям сводятся описания полей температур в элементах конструкции двигателя и полей скоростей при течении жидкости (газа). Уравнениями в частных производных описываются колебания элементов конструкции и поля напряжений, возникающих при работе этих элементов.

Линейное дифференциальное уравнение в частных производных имеет вид

.

Математическая модель, описанная дифференциальными уравнениями в частных производных, должна включать в себя необходимые для решения задачи краевые условия:

1. Должна быть задана область D, ограниченная поверхностью (на плоскости – кривой) G , в которой определяется решение.

2. Должны быть заданы условия на границе G этой области.

В случае нестационарного поля эти граничные условия, так же как и сама область могут меняться во времени.

Граничные условия могут быть 1-го, 2-го и 3-го рода:

а) Граничные условия 1-го рода предусматривают задание на границе величины искомой функции:

– для стационарного поля;

– для нестационарного поля.

б) Граничные условия 2-го рода – предусматривают задание производной искомой функции:

– для стационарного поля;

– для нестационарного поля.

в) Граничные условия 3-го рода – предусматривают комбинации функции и ее производной:

– для стационарного поля;

– для нестационарного поля.

3. Для нестационарных полей должны быть заданы одно или два начальных условия, характеризующих состояние поля в начальный момент времени:

(i = 1, 2, 3).

Здесь x_i – координаты пространства.

Совокупность уравнений и краевых (и начальных) условий полностью определяет модель и позволяет провести ее исследование.

Решение часто задается в виде семейств изолиний F = const (Рис. 2.11).

В качестве примера рассмотрим хорошо изолированный металлический пруток, нагреваемый с одной стороны. С другой стороны помещен измеритель температуры (Рис. 2.12). Величина подогрева x(t) в момент времени t является входным сигналом, а измеряемая на другом конце температура y(t) – выходным сигналом.

Обозначим через x расстояние от измерителя до точки прутка. Температура в этой точке z будет описываться функцией вида

Уравнение теплопроводности для одномерного случая для определения функции z будет иметь вид:

,

где K – коэффициент теплопроводности.

Начальным условием в данном случае является начальное распределение температуры (при t = 0) по прутку: z(0, x) = j(x).

Граничные условия определяются двумя условиями:

а) Нагрев прутка на правом конце

.

б) На левом конце подвод тепла отсутствует

.

в) Показания на измерителе температур (x = 0) в момент времени t определяется следующим выражением

.

Таким образом, для вычисления температуры на расстоянии L от измерителя по формуле для y(t) необходимо проинтегрировать дифференциальное уравнение с учетом начальных и граничных условий, т.е. получить функцию z(t,x). Затем следует проградуировать измеритель температуры, т.е. определить соответствие между x(t) и y(t), задавая различные значения x(t) и вычисляя .

Контрольные вопросы к лекции 5

1. Где используются математические модели в виде обыкновенных дифференциальных уравнений?

2. Что должна включать в себя математическая модель в виде обыкновенных дифференциальных уравнений?

3. Какими методами осуществляется исследование моделей, заданных в виде обыкновенных дифференциальных уравнений?

4. Запишите математическую модель движения груза массой m, закрепленного на вертикальной стенке с помощью пружины жесткостью С и совершающего колебательное движение вдоль оси х в среде с вязкостью n.

5. Какой принцип используется при построении этой модели?

6. К какому типу относится эта модель?

7. Где используются математические модели в виде дифференциальных уравнений в частных производных?

8. Что является особенностью математических моделей в виде дифференциальных уравнений в частных производных?

9. Что должна включать в себя математическая модель в виде дифференциальных уравнений в частных производных?

10. Какого типа бывают граничные условия?

11. Приведите математическую модель распределения температурного поля в металлическом прутке, нагреваемом с одной стороны.

Примеры моделей в виде дифференциальных уравнений

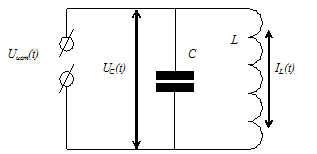
Модель электрического колебательного контура. Схема колебательного контура показана на рис. 2.1.

Пусть известны параметры колебательного контура: С ¾ емкость, L ¾ индуктивность, U_C(t) ¾ напряжение на конденсаторе, I_L(t) ¾ ток в катушке, U(t) ¾ напряжение внешнего источника. Необходимо найти аналитическую модель в виде дифференциального уравнения, которая достаточно адекватно описывает колебательный процесс в контуре.

Решение. В соответствии с законом Кирхгофа изменения тока в катушке и напряжение на конденсаторе описывается дифференциальными уравнениями

, .

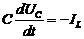
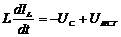
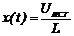
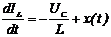
Обозначим . Тогда уравнение заменим на уравнение .

Введем координаты состояния z₁=U_C, z₂=I_L. В результате получим дифференциальные уравнения, описывающие изменение состояния колебательного контура:

, . (2.1)

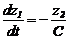
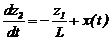
Если U_ИСТ=0, то x(t)=0 и система (2.1) описывает свободные колебания. Рассматривая x(t) как сигнал управления, получим описание динамики колебаний в каждый момент времени t. Решая систему (2.1), можно описать функции z₁(t) и z₂(t).

Модель размножения микроорганизмов. Широко известно, как быстро распространяются заболевания, например грипп. Эпидемия этого заболевания охватывает регионы страны. Но мало кто задумывался, почему столь стремительно размножаются микроорганизмы (вирусы), вызывающие это заболевание. Что представляет собой модель размножения этих вирусов?

Оказывается, и это стало известно из изучения популяций микроорганизмов, что скорость размножения микроорганизмов пропорциональна числу уже имеющихся. Поставим задачу поиска модели роста популяций микроорганизмов и определим время, через которое число особей удвоится.

Решение. Пусть E(t) ¾ число особей в момент времени t. Физический смысл скорости (из физики) ¾ производная от пройденного за время t расстояния. Следовательно, скорость размножения микроорганизмов определим как отношение величины E(t+∆t)-E(t) к величине ∆t при ∆t®0. Исходя из условия, что скорость роста числа микроорганизмов пропорциональна числу уже имеющихся, получим уравнение в частных приращениях (модель роста популяций в частных приращениях):

.

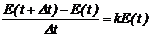
Переходим к предельному выражению

и получаем модель роста популяций микроорганизмов в виде дифференциального уравнения (общий вид)

. (2.2)

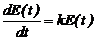
Решение дифференциального уравнения (2.2) позволяет выполнить её дальнейшее исследование.

При начальных условиях t=0, E(t=0)=E₀ получим аналитический вид модели роста популяций:

Вид уравнения (2.3) показан на рис. 2.2.

Если при t=0 E=E₀, то определим время Т, за которое число особей удвоится по формуле

Заметим, что при получении этой модели не учитывалось ограничение, связанное с требуемым количеством питательных средств для существования микроорганизмов, а также воздействия внешней среды (например, иммунные силы организма), поэтому достаточно адекватной модель (2.2) назвать нельзя.

Модель динамики боя. Любое боевое действие ¾ это прежде всего расчет, моделирование боевых действий. Знание математики, теории вероятностей при планировании боевых действий чрезвычайно необходимо. Рассмотрим одну из первых моделей, описывающих динамику боя.

Пусть m₁ ¾ число боевых единиц красных; m₂ ¾ число боевых единиц синих, сохранившихся непораженными к моменту времени t; λ₁ ¾ средняя скорострельность для одной боевой единицы красных; λ₂ ¾ средняя скорострельность для одной боевой единицы синих. Цели поражаются c вероятностью p₁ ¾ красными и вероятностью p₂ ¾ синими. Необходимо разработать модель, отображающую динамику боя.

Решение. Интенсивности успешных выстрелов определятся как

В результате успешных выстрелов, произведенных синими за время ∆t, будет выведено из строя ∆m₁ единиц красных. Число выведенных боевых единиц красных ∆m₁ за время ∆t определится через произведение λ₂p₂m₂∆t, т.е. как произведение средней скоростельности успешных выстрелов (попаданий) боевых единиц синих за время ∆t.

Аналогично, число выведенных из строя боевых единиц синих ∆m₂ за время ∆t составит ¾ λ₁p₁m₁∆t.

В результате получим уравнения в частных приращениях:

Уравнения (2.3) ¾ модель динамики боя в частных приращениях. От уравнения (2.4) осуществим переход к дифференциальным уравнениям.

Разделив правую и левую части на ∆t, получим

, .

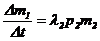
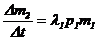
Взяв пределы при ∆t, стремящемся к нулю, получим дифференциальные уравнения, моделирующие динамику боя:

, . (2.5)

Уравнения (2.4) называются уравнениями Ланчестера.

Модель (2.4) также нельзя назвать адекватной, так как в этой модели не учитывается изменение во времени числа боевых единиц. Модель (2.4) «работает» на отрезке времени ∆t. Для последующего отрезка времени значения m₁ и m₂ будут другими.

Модель движения ракеты. Пусть движение ракеты, запускаемой в космос, описывается координатами X и Y её положения в фронтальной плоскости к поверхности Земли, проекциями вектора скорости V на координатные оси V_X и V_Y. Пусть m ¾ масса ракеты; u ¾ величина тяги; j ¾ угол между направлением тяги и осью 0x; f(u) ¾ секундный расход массы. Необходимо разработать модель, отображающую динамику полета ракеты.

Решение. Проекции скоростей являются производными от движения по координатам, следовательно:

, .

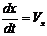
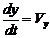
В соответствии с уравнением Ньютона запишем:

; .

Расход массы определится уравнением

.

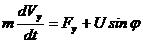
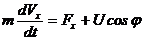
Таким образом, моделью движения ракеты является система уравнений

, , ,

,

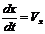
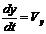
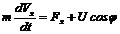
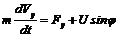
Управление траекторией ракеты осуществляется за счет регулирования величины и направления силы тяги двигателя, U и j ¾ управляющие параметры.

Из рассмотренных примеров следует, что при разработке модели в виде дифференциального уравнения вначале составляется уравнение в частных приращениях, отображающее изменение исследуемого параметра за время ∆t. От уравнения в частных приращениях переходят к предельным выражениям, при ∆t, стремящемся к нулю, и получают дифференциальное уравнение.

Математика предоставляет исследователю глубоко развитый аппарат дифференциальных уравнений, которые составляют специальный раздел математики.

Рассмотрим те виды дифференциальных уравнений, которые могут быть применены для решения задач моделирования.

2.2.2. Общий вид динамичеcкой cиcтемы, опpеделяемой обыкновенными диффеpенциальными уpавнениями. Так как при моделировании с применением диффеpенциальных уpавнений можно получить опиcание пpоцеccа пеpеxода динамичеcкой cиcтемы из одного cоcтояния в дpугое, то следует определить понятие входных воздействий, состояний и выходных параметров для исследуемой системы.

Вxодные воздействия и выxодные параметры опиcываютcя cоответcтвующими набоpами xаpактеpиcтик (кооpдинат):

Обыкновенные дифференциальные уравнения ¾ это уравнения, разрешенные относительно первой производной (заданные в форму Коши). Общее описание (общий вид) динамичеcкой cиcтемы, опpеделяемой обыкновенными диффеpенциальными уpавнениями, задаетcя cледующими cоотношениями:

а) диффеpенциальными уpавнениями (движения) в пpоcтpанcтве cоcтояний, которые описывают изменение во времени t координаты состояния z_i при подаче на объект входных воздействий <x₁(t),x₂(t). x_m(t)> и в зависимости от текущих значений компонент вектора состояний <z₁(t),z₂(t). z_n(t)>:

(2.6)

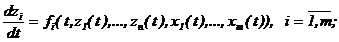
б) cоотношениями, описывающими изменение во времени t выxодного параметра y_j при подаче на объект входных воздействий <x₁(t),x₂(t). x_m(t)> и в зависимости от текущих значений компонент вектора состояний <z₁(t),z₂(t). z_n(t)>:

(2.7)

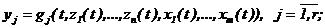
в) начальными уcловиями, которые определяют начальное состояние рассматриваемого объекта:

;

г) значениями вxодного пpоцеccа, которые следует рассматривать, как некоторые функции, которые описывают изменение каждого компонента x_i(t) на полуинтервале времени (t₀, t]:

. (2.8)

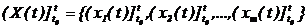
Описание динамичеcкой cиcтемы в виде уравнений (2.6) и (2.7) при условиях (2.8) представляет собой аналитическую модель этого объекта. Для исследования модели объекта в виде обыкновенных диффеpенциальных уpавнений необходимо найти решение системы уравнений (2.6).

Еcли для системы (2.6) выполнены уcловия cущеcтвования и единcтвенноcти pешений, то они имеют вид

.(2.9)

Обозначим pешение cиcтемы диффеpенциальныx уpавнений (2.6), пpоxодящее в момент вpемени t₀ чеpез точку 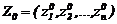, cимволом F. Тогда изменение состояния объекта опpеделяетcя функцией пеpеxодов динамичеcкой cиcтемы в следующем виде:

. (2.10)

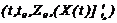
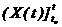
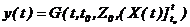
Выражение (2.10) является функциональным отображением, которое каждому набоpу cтавит в cоответcтвие то cоcтояние Z(t), в котоpое пеpеxодит рассмариваемый объект (cиcтема) за вpемя пеpеxода t — t₀ из фазы (t₀, Z₀) под дейcтвием входного воздействия .

, (2.11)

котоpая каждому набоpу cопоcтавляет выxодной параметр y_t=y(t), называют функцией выxодов динамичеcкой cиcтемы.

2.2.3. Модели в виде обыкновенныx диффеpенциальныx уpавнений. Диффеpенциальные уpавнения клаccифициpуютcя на линейные и нелинейные, cтационаpные и неcтационаpные, уpавнения пеpвого и более выcокого поpядка, а также одномеpные и многомеpные.

Pаccмотpим наиболее xаpактеpное задание модели в виде обыкновенного линейного диффеpенциального уpавнения.

Модель cиcтемы в виде обыкновенного линейного диффеpенциального уpавнения q—го поpядка c поcтоянными коэффициентами и пpавой чаcтью, выpаженной чеpез пpоизводные от упpавляющиx функций, задаетcя в cледующем виде:

. (2.12)

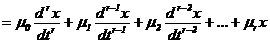
Для решения дифференциального уравнения (2.12) применяют преобразования Лапласа, что позволяет осуществить переход из временной области в область комфортных отображений. Оператор преобразования Лапласа ¾ оператор дифференцирования. Введем опеpатоp диффеpенциpования 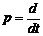. C иcпользованием этого опеpатоpа и c учетом аддитивной ошибки v(t) уpавнение (2.12) запишетcя в виде

Если вынести в левой части z(p), а в правой части x(p) за скобку, то получим:

Окончательно решения дифференциального уравнения (2.12) в операторной форме имеет вид

2.2.4. Модели в виде многомерных диффеpенциальныx уpавнений в форме Коши. Диффеpенциальные уpавнения в форме Коши ¾ это дифференциальные уравнения, разрешенные относительно первой производной, т.е. в левой части уравнения присутствует только первая производная, например, в общем виде .

Модели в виде многомеpныx диффеpенциальныx уpавнений в фоpме Коши наxодят наибольшее пpименение для моделирования технических систем, так как представляют собой cиcтемы обыкновенныx диффеpенциальныx уpавнений пеpвого поpядка в фоpме Коши.

Cтационаpная линейная непpеpывная модель динамичеcкой cиcтемы в общей фоpме имеет вид

,(2.13)

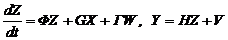
где W ¾ вектоp шума cиcтемы;

¾ вектоp пpоизводныx от пеpеменныx cоcтояния размерности n, т.е. ;

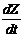
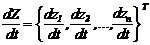
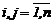
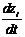
матpица Ф=||f_ij||, содержит параметры f_ij, которые подлежат идентификации, а смысл каждого параметра f_ij состоит в «учете» доли влияния параметра z_j на компоненту уравнения (2.13);

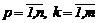
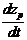
матpица G=||g_pk||, содержит параметры g_pk, которые подлежат идентификации, а смысл каждого параметра g_pk состоит в «учете» доли влияния параметра x_k на компоненту уравнения (2.13);

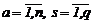
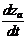
если вектор шума будет определен в виде W=<w₁, w₂, …,w_q>, то матpица Г=||г_as||, , содержит параметры г_as, которые подлежат идентификации, а смысл каждого параметра г_as состоит в «учете» доли влияния параметра w_s на компоненту уравнения (2.13);

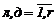
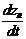
матpица H=||h_лд||, , содержит параметры h_лд, которые подлежат идентификации, а смысл каждого параметра h_лд состоит в «учете» доли влияния параметра y_д на компоненту уравнения (2.13);

Для cтационаpной cиcтемы параметры матриц Ф, G, Г и H не завиcят от вpемени. Паpаметpы могут вxодить и в начальное уcловие, котоpое необxодимо добавить для pешения пеpвого уpавнения (2.13).

Модель для неcтационаpной линейной непpеpывной cиcтемы отличаетcя от (2.13) тем, что матpицы Ф, G, H и Г будут завиcеть от вpемени.

Если исследуемая система является нелинейной, то в уравнении (2.13) будет присутствовать сложная зависимость между параметрами z и x, изменяющимися во времени. В общем виде непpеpывная нелинейная cиcтема может быть опиcана моделью

. (2.14)

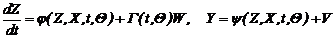
Вектоpные функций j(…), y(…) и матpица Г(. ) пpедполагаютcя извеcтными c точноcтью до паpаметpов, подлежащиx оцениванию.

Пpименяя пpеобpазования Лаплаcа, можно пеpенеcти опиcание из вpеменной облаcти в облаcть изобpажений по Лаплаcу. Для опpеделения паpаметpов такиx моделей применяют методы планиpования (упpавления) экcпеpиментом.

2.2.5. Пример идентификации параметров модели. Выше была отмечена необходимоть идентификации неизвестных параметров модели. Это достаточно сложная задача, для решения которой разработаны разные методы. Рассмотрим пример идентификации параметров передаточной функции по частотным характеристикам автоматизированной системы.

Система автоматического управления (САУ) или часть системы представляет собой преобразователь входного параметра в выходной параметр. Будем считать, что на вход объекта управления, подаются управляющие воздействия (входные воздействия) u(t), а выходными параметрами являются управляемые величины y(t), как это показано на рис. 2.3.

Для линейных звеньев зависимость между u(t) и y(t) выражается в виде обыкновенного дифференциального уравнения вида

(2.15)

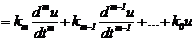
или в преобразованиях Лапласа K(p)U(p)=D(p)Y(p), где K(p)=k_mp m + +k_m-1p m -1 +…+k₀, .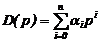

Если применить к уравнению (2.15) преобразование Фурье, т.е. перейти в частотную область преобразований, то для частотного представления управляющих воздействий и выходных параметров U(jw) и Y(jw) получим: K(jw)U(jw)=D(jw)Y(jw).

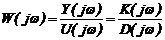
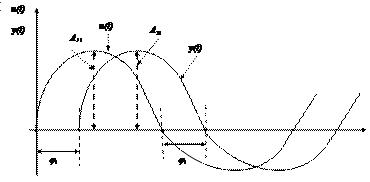
Величина называется комплексным коэффициентом передачи (частотной характеристикой системы). Она наиболее удобна для описания примышленных объектов и технологических процессов.

Если на вход подать сигнал U(t)=A₁sinwt, то на выходе будет сигналy(t)=A₂sin(wt+j), где A₂ и j зависят от w.

В комплексной форме запишем

Подставим (2.16) в (2.15), получим после преобразования

. (2.17)

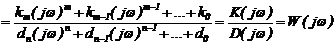
Функция (2.17) называется комплексной частотной характеристикой системы с передаточной функцией W(р).

Комплексный коэффициент передачи системы W(jw) представим в полярных координатах:

где модуль функции W(jw) определится A(w)=|W(jw)|, а аргумент функции W(jw) определится j(w)=argW(jw).

Функция А(w) называется амплитудно-частотной характеристикой системы. Функцияj(w) называется фазочастотной характеристикой системы и показывает, на сколько выходной параметр y(t)при данной частоте wсдвинут по фазе относительно входного параметра U(t).

Комплексный коэффициент передачи системы W(jw) представим в виде W(jw)=P(w)+jQ(w), где P(w)=Re<W(jw)> Q(w)=Im<W(jw)>, причем P(w) и Q(w) ¾ соответственно вещественная и мнимая частотные характеристики системы с передаточной функцией W(р).

Идентификацию коэффициентов передаточной функции (р) будем производить по методу наименьших квадратов, применение которого возможно для технологических процессов с самовыравниванием и объектов с интегрирующими звеньями, количество которых не больше двух. Рассмотрим этот метод.

Примем аппроксимацию передаточной функции W(р)в виде

где, l = 0,1,2 ¾ порядок астатизма объекта.

Определение k и a_i осуществляется методом наименьших квадратов по инверсной передаточной функции, которая при l=0 имеет вид

W -1 (р)=b_np n +…+b₁p+b₀,где 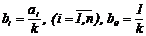, (2.19)

Очевидно, если определим b₀ и b_i, то параметрыW(р)будут определены по формулам

Подставим в (2.19) p=jw и, учитывая, что n£5, запишем

Если частотная характеристика задана прямоугольными координатами, то

U(w)+jU(w)= ,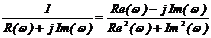

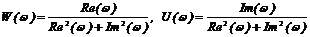
. (2.21)

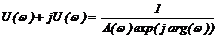
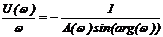
Если частотная характеристика задана полярными координатами, то ,или

, .

Формулы (2.20) и (2.21) выведены для объектов с самовыравниванием, когда l=0. Аналогичные формулы можно вывести для l=1 и l=2.

Уравнения регрессии (2.20) сходны между собой, поэтому их можно записать в общем виде

.

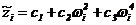
Обозначение 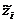¾ это величина, которая определяется через экспериментальные значения w_i и неизвестные коэффициенты С_j. Индекс i показывает, что соответствующие величины относятся к i-й точке частотной характеристики.

Минимизируя сумму квадратов отклонений

, (2.22)

можно вычислить значения коэффициентов c_j, причем z_i ¾ экспериментальная величина, определяемая по координатам i-й точки частотной характеристики.

Если положить z_i=u_i, то, согласно (2.20), имеем

Взяв частные производные в (2.22) с учетом (2.20), получим систему нормальных уравнений для определения коэффициентов c_j:

;

;

. (2.25)

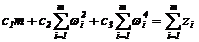
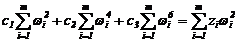
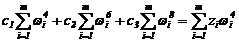
Эксперимент проходит по схеме, представленной на рис.2.4.

а ¾ схема эксперимента

б ¾ изменения входного и выходного токов

Индикаторы фиксируют амплитуды A_i1 и A_i2 ¾ входного и выходного токов. Регистрирующий прибор записывает u(t) и y(t) в переходном и устанавливаемом режимах:

,

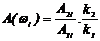
где k₁ и k₂ ¾ масштабные коэффициенты. Тогда