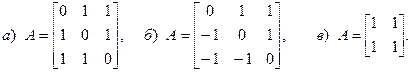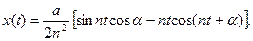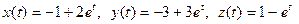Моделирование физических задач с применением теории дифференциальных уравнений средствами MathCad и Maple
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Комитет общего и профессионального образования
Ленинградской области
Автономное образовательное учреждение
высшего профессионального образования
«Ленинградский государственный университет имени А.С.Пушкина»
Факультет математики и информатики
Кафедра информатики и вычислительной математики
КУРСОВАЯ РАБОТА
по дисциплине «Компьютерное моделирование»
Моделирование физических задач с применением теории дифференциальных уравнений средствами MathCad и Maple
студентки 4 курса,
факультета математики и информатики
(ФИО, уч степень, уч звание, долж-ть)
Оглавление
Глава 1. Теоретические сведения из теории дифференциальных уравнений и численных методов 7
§1.1. Теоретические сведения из теории дифференциальных уравнений 7
п.1. Основные сведения 7
п.2. Дифференциальное уравнение первого порядка 8
п.4. Решение дифференциальных уравнений (общее и частное решения) 9
п.5. Уравнение с разделяющимися переменными 10
§1.2. Теоретические сведения из численных методов 12
п.1. Метод Рунге-Кутта 12
п.2. Метод Эйлера 15
п.3. Погрешность методов Рунге-Кутта и Эйлера 16
Глава 2. Алгоритм построения модели и аналитическое решение построенного дифференциального уравнения 17
§2.1. Аналитическое решение построенного обыкновенного дифференциального уравнения 17
§2.2. Технология решения ОДУ в пакетах Mathcad и Maple 19
§2.3. Символьное решение в Maple 21
§2.4. Численное решение в Mathcad 24
§2.5. Сравнительная характеристика точного и численного решений 37
§2.6. Анализ результатов и выводы 39
Введение
Реальные объекты окружающего мира многообразны и сложны. Они не существуют отдельно, а находятся в некоторых отношениях, которые составляют сложную систему. Для выявления различных закономерностей в сложных системах используют моделирование.
Моделирование – это способ исследования, при котором изучение реальной системы заменяется изучением ее модели, а полученные результаты распространяются на исходные объекты.
В данной курсовой работе мы будем рассматривать математическое и компьютерное моделирование.
Математическое моделирование описывает модели на математическом языке. Выбор математической модели зависит от предметной области, в рамках которой строится и реализуется данная модель.
Далее мы будем рассматривать дифференциальную модель решения физической задачи.
Компьютерное моделирование подразумевает математическую модель, реализованную средствами какой-либо программной среды.
К основным этапам компьютерного моделирования относятся:
постановка задачи, определение объекта моделирования;
разработка концептуальной модели, выявление основных элементов системы и элементарных актов взаимодействия;
формализация, то есть переход к математической модели;
создание алгоритма и написание программы;
планирование и проведение компьютерных экспериментов;
анализ и интерпретация результатов.
В данной курсовой работе дифференциальная модель будет реализована средствами MathCad и Maple .
Система MathCAD представляет, широкие возможности для реализации различных видов дифференциальных уравнений:
встроенные функции для численного решения;
вычисление решений по итерационным формулам;
вычисление аналитических решений по готовым формулам;
запись алгоритма решения с помощью средств программирования системы MathCAD .
Для решения дифференциальных уравнений и систем дифференциальных уравнений в Maple пользователю предлагается большой набор функций, основное количество которых расположено в библиотеке DEtools . Например, для решения дифференциального уравнения первого порядка мы использовали встроенную команду dsolve .
Цели и задачи моделирования:
получение аналитического, частного и символьного решений полученного дифференциального уравнения;
построение графиков найденных решений;
анализ полученных результатов.
Цели и задачи курсовой работы:
по данным физической задачи построить дифференциальную модель;
реализовать ее средствами MathCad и Maple ;
решить задачу аналитически, символьно и численно;
сравнить полученные результаты и сделать выводы.
Постановка задачи
Условие задачи: Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости движения. Найти время движения пули через брус.
L =12 см=0.12 м – толщина бруса;
v 0 =200 м/с — скорость, с которой пуля влетает в брус;
v 1 =60 м/с — скорость, с которой пуля вылетает из бруса.
Разбор условия задачи и составления чертежа, поясняющего суть задачи;
Составление дифференциального уравнения рассматриваемой задачи;
Интегрирование составленного дифференциального уравнения;
Нахождение общего и частного решения задачи;
Вывод общего закона рассматриваемого процесса и числовое определение искомых величин;
Анализ ответа и проверка исходного положения задачи.
Сравнить полученный ответ с начальными данными. Оценить возможность существования полученного решения. Например, скорость движения пули через брус не может быть больше начальной скорость пули.
Найти численное решение в MathCad . Сравнить полученное численное решение с аналитическим решением, с помощью погрешности. Оценить полученные погрешности. Например, погрешность метода Рунге-Кутта не должна превосходить (-5) степень, а погрешность метода Эйлера – (-2) степени. Если погрешности в результате решения поставленной задачи получились больше указанных значений – решение неверно.
Проанализировать символьное решение в Maple , построив графики полученных решений. График символьного решения должен отличаться от графика точного решения с погрешностью, заданного метода. Т.к. на графике сложно увидеть погрешность используемых методов (например, Рунге-Кутта), то графики точного и символьного решения должны совпадать.
Глава 1. Теоретические сведения из теории дифференциальных уравнений и численных методов
§1.1. Теоретические сведения из теории дифференциальных уравнений
п.1. Основные сведения
Дифференциальные уравнения являются одним из основных математических понятий, наиболее широко применяемых при решении практических задач. Причина этого состоит в том, что при исследовании физических процессов. Решение различных прикладных задач, как правило, не удается непосредственно найти законы, связывающие величины, характеризующие исследуемые явления. Обычно легче устанавливаются зависимости между теми же величинами и их производными или дифференциалами. Соотношения такого рода и называются дифференциальными уравнениями. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Дифференциальным уравнением называется уравнение, связывающее независимую переменную t , неизвестную функции x ( t ) этой независимой переменной и ее производные

где F – функция указанных аргументов, заданная в некоторой области их изменения.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Уравнение (1) является уравнением n -го порядка.
В теории дифференциальных уравнений изучаются и такие уравнения, которые содержат несколько независимых переменных, искомую функцию и частные производные от искомой функции по независимым переменным. Такие уравнения называются дифференциальными уравнениями с частными производными. Например, таким уравнением будет
где 
Решения и интегральные кривые:
Всякая функция 




будет решением уравнения 



Иногда решения получают в неявном виде
или в параметрической форме

График решения дифференциального уравнения называется интегральной кривой этого уравнения. Часто ради краткости интегральную кривую называют решением.
п.2. Дифференциальное уравнение первого порядка
Рассмотрим основные понятия, относящиеся к уравнениям первого порядка общего вида. Согласно определению уравнение первого порядка имеет вид:

определенная и непрерывная дифференцируемая в интервале 


справедливое для всех значений х из интервала 


п.3. Задача Коши
Во многих вопросах теоретического и прикладного характера требуется среди всех решений дифференциального уравнения найти решение

удовлетворяющее условию (условию Коши)


где 





Геометрически это означает, что требуется найти интегральную кривую, проходящую через заданную точку 
Условие (2) называется начальным условием решения (1), а числа 



п.4. Решение дифференциальных уравнений (общее и частное решения)
Дадим определение общего решения любого уравнения первого порядка в нормальной форме 
Пусть D есть некоторая область на плоскости ( х,у) , через каждую точку которой проходит одна и только одна интегральная кривая уравнения 


1) равенство 
2) функция 


Основное свойство общего решения 




Решение y = y ( x ) , в каждой точке которого сохраняется единственность решения задачи Коши, называется частным решением. Решение, содержащееся в формуле общего решения 
п.5. Уравнение с разделяющимися переменными
Если дифференциальное уравнение имеет вид:

так что коэффициенты при dy и dy являются произведениями двух функций, из которых одна зависит только от х , а другая – только от у, то в нём можно разделить переменные. Поэтому уравнение 
§1.2. Теоретические сведения из численных методов
Решить дифференциальное уравнение 





Таким образом, численные методы позволяют вместо нахождения функции 

п.1. Метод Рунге-Кутта
Разностной схемой задачи Коши
будем называть следующую систему линейных алгебраических уравнений относительно неизвестных у 0 , у 1 ,…,у n :
Аппроксимацией дифференциальной задачи разностной схемы на решении y = y ( x ) называется замена задачи Коши задачей
Метод, предложенный К.Рунге (1905) и развитый М. Кутта (1911), позволяет строить разностные схемы различного порядка точности. Они являются наиболее употребительными в практических вычислениях.
Запишем задачу Коши следующим образом:

Идея составления разности схемы Рунге – Кутта для дифференциальной задачи (1) заключается в следующем:
Пусть значение 




где 
Составим разностную схему:

где 
Разностной схемой Рунге – Кутта порядка m будем называть разностную схему (2).
Выбор коэффициентов 

Теперь порядок аппроксимации дифференциальной задачи разностной схемой будет определяться величиной

Коэффициенты 


Таким образом, s – это максимальный порядок производной, равной 0 при h =0.
Воспользуемся формулой Тейлора в окрестности точки х =0 с остаточным членом в форме Коши для вычисления 

Таким образом, порядок аппроксимации будет равен s , т.к.

Запишем разностные схемы при m = 1, 2, 3 и 4 соответственно.
п.2. Метод Эйлера
Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Пусть дано дифференциальное уравнение первого порядка

с начальным условием

Требуется найти решение уравнения (1) на отрезке 
Разобьем отрезок 




Выберем 



Если в последнем интеграле подынтегральную функцию на участке 


Тогда формула (3) примет вид


Обозначив 


Продолжая этот процесс, и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной ее значению в начале участка, получим таблицу решений дифференциального уравнения на заданном отрезке 
п.3. Погрешность методов Рунге-Кутта и Эйлера
Важным этапом численного решения задачи Коши является оценка погрешности используемого метода.
Величина погрешности на сетке отрезка [ a ; b ] оценивается величиной

где 


Часто аналитическое решение дифференциального уравнения неизвестно (или поиск его сложен), а теоретически оценить погрешность достаточно трудоемко. Поэтому на практике для оценки погрешности решения, найденного на сетке с шагом h /2 , в точке x i [ a ; b ] используют приближенное равенство – правило Рунге:
где p – порядок точности численного метода (для метода Эйлера р=1 , для метода Рунге-Кутта – р=4 ), 


Таким образом, оценка полученного результата требует проводить вычисления дважды: один раз с шагом h , другой – с шагом h /2 . за оценку погрешности решения, вычисленного с шагом h /2 , принимают величину
Погрешность метода Эйлера не должна превосходить (-2) степени. Погрешность метода Рунге-Кутта не должна превосходить (-5) степени.
Глава 2. Алгоритм построения модели и аналитическое решение построенного дифференциального уравнения
§2.1. Аналитическое решение построенного обыкновенного дифференциального уравнения
Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает, пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости. Найти время движения пули через брус.
Пусть v 0 – скорость пули до вхождения в брус, v 1 – скорость пули после вхождения в брус, T – время движения пули через брус.
На пулю действуют силы тяжести 


Запишем второй закон Ньютона для центра масс пули:
Выберем ось x сонаправлено с вектором скорости пули.
Составим дифференциальное уравнение:
где С 1 – произвольная константа.
По определению 

где С 1 и С 2 – произвольные константы.
То есть, искомое время T равно:
Ответ: 0,001163 секунд – время движения пули через брус.
Классифицируем данную модель по разным основаниям:
по целям моделирования – дескриптивная модель
по учету фактора времени – динамическая модель
по оператору модели – функциональная модель
по переменным и параметрам моделирования – детерминированная модель
по методам реализации – алгоритмическая модель
по характеру постановки задачи – задача анализа.
§2.2. Технология решения ОДУ в пакетах Mathcad и Maple
Для решения дифференциальных уравнений система Mathcad предоставляет широкие возможности:
встроенные функции для численного решения;
вычисление решений по итерационным формулам;
вычисление аналитических решений по готовым формулам;
использование преобразований Лапласа для решения уравнений в частных производных;
запись алгоритма решения с помощью средств программирования системы Mathcad .
Одним из преимуществ компьютерного решения дифференциальных уравнений в системе Mathcad является возможность предоставления получаемых результатов в графическом виде, что позволяет получать наиболее полную информацию о поведении решения и исследовать его.
Рассмотрим встроенные функции Mathcad, предназначенные для решения дифференциальных уравнений. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы, по крайней мере, следующие величины, необходимые для поиска решения:
набор точек, в которых нужно найти решение;
само дифференциальное уравнение, записанное в некотором специальном виде.
В данной курсовой работе будет рассмотрена одна встроенная функция, предназначенная для решения обыкновенных дифференциальных уравнений методом Рунге-Кутта:
Она предназначена для решения систем обыкновенных дифференциальных уравнений в форме Коши методом Рунге-Кутта четвёртого порядка с фиксированным шагом.
y – вектор начальных условий размерности n , где n – порядок обыкновенного дифференциального уравнения. Для обыкновенного дифференциального уравнения первого порядка вектор начальных условий вырождается в одну точку y 0 .
x1, x2 – граничные точки интервала, на котором ищется решение дифференциального уравнения. Начальные условия, заданные в векторе y — это значение решения в точке x1 .
N – число точек (не считая начальной точки), в которых ищется приближённое решение. Число строк в матрице, возвращаемой функцией rkfixed , равно N+1 .
D(x,y) — вектор функция, состоящая из n элементов и содержащая первые производные искомых функций, т.е. правые части системы обыкновенных дифференциальных уравнений, представленных в нормальной форме (форме Коши). Для обыкновенного дифференциального уравнения первого порядка вырождается в скалярную функцию.
В результате решения получается матрица, состоящая из n – столбцов ( n – порядок ОДУ или число элементов в вектор-функции D (x, y ) , где первый столбец содержит точки, в которых ищется приближённое решение, оставшиеся столбцы содержат для обыкновенного дифференциального уравнения 1-го порядка: значения найденного приближённого решения y(x) в соответствующих точках 1-го столбца.
Для решения обыкновенного дифференциального уравнения в пакете M aple предназначена функция dsolve (deqn, var, opt) , где
deqn — одно дифференциальное уравнение n -ого порядка или система дифференциальных уравнений первого порядка (заданная в виде множества),
var — переменная или переменные, относительно которых ищется решение,
opt — необязательный аргумент, в котором можно указать вид представления решения:
При решении задачи Коши выражение deqn должно иметь структуру множества и содержать (помимо уравнения или системы уравнений) начальные условия.
§2.3. Символьное решение в Maple
Запишем условие задачи и исходные данные:
Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает, пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости. Найти время движения пули через брус.
При решении задачи используется два дифференциальных уравнения, в результате мы получаем закон изменения скорости и закон перемещения:
Запишем дифференциальное уравнение:
Найдем его общее решение:
Поставим в найденное общее решение начальное условие v 0=200 м/с:
В результате мы получили частное решение закона изменения скорости.
Продифференцируем полученное для скорости общее решение:
Подставим в полученное уравнение начальное условие х=0:
Для получения частного решения подставим в полученное уравнение значение константы С=1/200:
В результате получили частное решение закона перемещения.
Найдем численное решение для закона изменения скорости и закона перемещения:
Чтобы обратиться к переменным h и T используем функцию op [ i , e ] , которая выделяет операнд под номером i из выражения е .
Построим график полученного решения:
Закон изменения скорости:
Warning, the name changecoords has been redefined
§2.4. Численное решение в Mathcad
§2.5. Сравнительная характеристика точного и численного решений
Сравнивать полученные решения будем с помощью оценки погрешности и графическим методом.
По графикам видно, что решения методом Рунге-Кутта и методом Эйлера совпадают с точным решением.
Погрешность метода Рунге-Кутта по правилу Рунге:
Закон изменения скорости:
Погрешность метода Рунге-Кутта с точным решением:
Закон изменения скорости:
Погрешность метода Эйлера по правилу Рунге:
Закон изменения скорости:
Погрешность метода Эйлера с точным решением:
Закон изменения скорости:
Погрешности, полученные в результате решения, удовлетворяют требованиям. (Погрешность метода Эйлера не должна превосходить (-2) степени. Погрешность метода Рунге-Кутта не должна превосходить (-5) степени).
§2.6. Анализ результатов и выводы
Проанализируем решение, полученное аналитически и численными методами.
При решении дифференциального уравнения методом Рунге-Кутта мы получили наиболее точное решение. График этого решения совпадает с аналитическим решением. Метод Эйлера считается наименее точным, график его решения совпадает с точным решением при большом уменьшении шага.
Таким образом, получилось, что когда затруднён расчёт аналитического решения целесообразно использовать метод Рунге-Кутта.
Заключение
В данной курсовой работе были рассмотрены три метода решения дифференциального уравнения: аналитическое, численное (метод Рунге-Кутта и метод Эйлера). Так же в курсовой работе показано как оценивать погрешность при вычислениях численными методами. Погрешность можно оценить аналитически и графически.
При выполнении курсовой работы был сделан вывод о том, что метод Рунге-Кутта является наиболее точным.
При работе над задачей были использованы средства MathCad и Maple , т.к. они предоставляют широкие возможности для решения дифференциальных уравнений. Данные средства, благодаря встроенным функциям, позволяют получить численные решения, а так же аналитическое решение по готовым формулам.
В ходе выполнения работы мы получили как общее, так и частное решения. Результат представили не только в аналитическом, но и в графическом виде, для более наглядного представления полученных решений.
Список литературы
Алексеева Т.А. Компьютерное моделирование в пакете Mathcad (дифференциальные уравнения). Методические указания к курсовой работе. – СПб: Ленинградский государственный университет им. А.С.Пушкина, 2005. – 28с.;
Алексеева Т.А. Информационные технологии в математике. Часть I . (Система Mathcad ). Учебное пособие. 4-е изд. – СПб: Ленинградский государственный университет имени А.С.Пушкина, 2010. – 60 с.;
Алексеева Т.А., Жихарева А.А. Информационные технологии в математике. Часть II . (Пакет Maple ). Учебное пособие. – СПб: АОУ ВПО «Ленинградский государственный университет имени А.С.Пушкина», 2010. – 36с.
Бахвалов Н.С. Численные методы. – 2-е изд. – М.: Наука, 1975. – 632 с.
Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах: Учебное пособие. – М.: Изд-вл МАИ, 2000. – 380 с.
МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дата добавления: 2015-06-12 ; просмотров: 8135 ; Нарушение авторских прав
Цель работы: освоение методики моделирования линейных дифференциальных уравнений в системе MATLAB и SIMULINK.
I. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Линейное дифференциальное уравнение.
Многие физические процессы, такие как колебания маятника, движение стрелки гальванометра, изменение высоты при посадке самолета, процессы в электрическом колебательном контуре могут быть описаны линейным однородным дифференциальным уравнением второго порядка
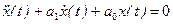
Здесь а0, а1 – постоянные коэффициенты, определяющие характер процесса, точкой обозначается производная по времени. Амплитуда переменной x(t) зависит от начальных условий, например, от начального отклонения x0 маятника и его начальной скорости 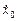
Вид теоретического решения дифференциального уравнения (1) определяется корнями его характеристического полинома
Если корни вещественные и различные р1 = a1`, р2 = a2`, то решение имеет вид
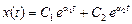
Если корни комплексные р1,2 =a ± ib , то решение имеет вид
Постоянные С1 и С2 находят, подставляя начальные условия в выражения для x(t) и 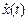
Пример 1. Дано дифференциальное уравнение
Его характеристическое уравнение p 2 + 2p + 2 = 0 имеет корни 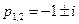
Дифференцируя, находим выражение для 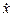
При t = 0 с учетом начальных условий получаем C1 = 2, С2 = 1. Следовательно,
Эффективным средством решения дифференциальных уравнений является численное моделирование в одном из математических пакетов (MATHCAD, MATLAB, SIMULINK и др.). График решения x(t) наблюдается на экране дисплея. В пакете MATLAB для этой цели имеются команды initial, lsim, ode23, ode45, dsolve. Дополнительныe возможности для пользователя предоставляет моделирование в SIMULINK.
1.2. Структурное моделирование линейных дифференциальных уравнений.
При структурном моделировании дифференциальных уравнений в пакете SIMULINK необходимо составить схему моделирования. На ней изображаются вычислительные блоки (усилители, сумматоры, интеграторы) и связи между ними. При проведении моделирования эта схема набирается на экране дисплея с помощью мыши или клавиатуры. По своему смыслу этот процесс аналогичен вводу программы, однако он более прост и нагляден. Подробная информация о реализации таких схем в SIMULINK имеется в разделе 3 учебного пособия Мироновского Л.А., Петровой К.Ю. «Введение в MATLAB» (ГУАП, 2006).
Рассмотрим методику составления схемы моделирования на примере однородного линейного дифференциального уравнения второго порядка
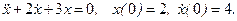
Для построения схемы моделирования воспользуемся методом понижения производной (методом Кельвина). В нем можно выделить четыре шага.
Шаг 1. Разрешаем исходное уравнение относительно старшей производной. В частности для уравнения (2) получаем 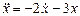
Шаг 2. Полагаем старшую производную известной и выполняем ее последовательное интегрирование, получая все низшие производные и саму переменную х. В случае уравнения (2) для этого потребуется два последовательно включенных интегратора, на выходах которых получим сигналы 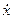
Шаг 3. Формируем старшую производную, используя уравнение, полученное на первом шаге. В нашем примере для этого потребуется сумматор, складывающий сигналы 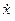
Шаг 4. Объединяем схемы, полученные на втором и третьем шагах, в общую схему моделирования, указываем начальные условия интеграторов.
Применение этой методики для уравнения (2) приводит к схеме, показанной на рис. 1. Она содержит два интегратора, два масштабных усилителя и сумматор (обозначен кружочком).
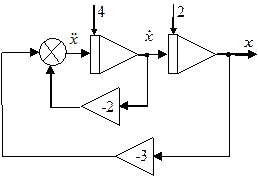 Рис. 1. Схема моделирования уравнения (2) Рис. 1. Схема моделирования уравнения (2) |
Выходной сигнал схемы подается на имитатор осциллографа (блок Scope) или передается в рабочее пространство MATLAB (блоки OUT или ToWorkspase).
1.3. Системы линейных дифференциальных уравнений первого порядка.
Многие технические объекты можно описать системой n линейных дифференциальных уравнений первого порядка:
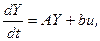
где и – входной сигнал; Y – вектор-столбец выходных переменных yi; b – вектор-столбец коэффициентов bi; A – квадратная матрица коэффициентов aij, 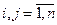
Например, при моделировании летательного аппарата составляющими вектора Y могут быть текущие координаты самолета и скорости их изменения, тогда матрица A будет характеризовать динамику самолета, а слагаемое bи описывать управляющие воздействия, формируемые летчиком или автопилотом.
Один из методов решения системы дифференциальных уравнений основан на предварительном переходе от системы (3) к одному уравнению n-го порядка. Для этого из уравнений системы и из уравнений, полученных их дифференцированием, исключают все переменные кроме одной. Для нее получают одно дифференциальное уравнение. Решая его, определяют эту переменную, а остальные находят, по возможности, без интегрирования.
Пример 2. Дана система из двух дифференциальных уравнений
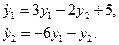
После дифференцирования первого уравнения получаем:
Чтобы исключить у2, вычтем отсюда удвоенное первое уравнение системы (4):
Мы получили линейное неоднородное дифференциальное уравнение второго порядка. Общее решение этого уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения 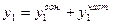
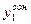
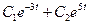
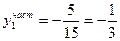
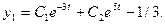
Для определения постоянных коэффициентов С1 и С2 используют начальные условия системы. Аналогичным образом этот метод применяется и для систем уравнений более высоких порядков
1.4. Моделирование системы линейных дифференциальных уравнений.
Если задача описывается системой дифференциальных уравнений первого порядка, то для ее моделирования по методу понижения производной достаточно составить схемы для каждого уравнения отдельно. Например, схема моделирования системы уравнений (4) будет иметь вид, показанный на рис. 2.
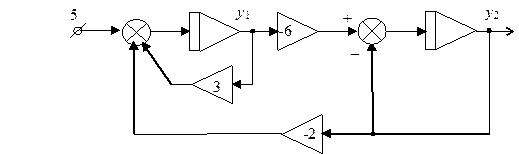 Рис. 2. Схема моделирования системы уравнений (4) Рис. 2. Схема моделирования системы уравнений (4) |
Для наблюдения графиков сигналов у1(t), у2(t) в SIMULINK используется блок осциллографа SCOPE, а для наблюдения фазовой траектории у2 = f (у1) – блок осциллографа XY Graph.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Теоретическое решение уравнения (1) при заданных значениях а0, а1 и начальных условиях x(0) = 5, 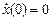
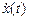
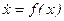
2. Схема моделирования заданного уравнения применительно к SIMULINK.
Теоретическое решение системы дифференциальных уравнений (3) для случая
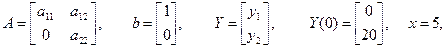
Схема моделирования исходной системы уравнений применительно к SIMULINK.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Набрать в SIMULINK схему моделирования уравнения (1), установить коэффициенты и начальные условия.
- Получить осциллограммы x(t),
и
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Набрать схему моделирования системы уравнений (3), установить коэффициенты и начальные условия (5).
- Получить осциллограммы у1(t), у2(t) и у2 = f(y1), сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Выполнить моделирование системы уравнений (3) в MATLAB, используя команду lsim. Cравнить графики, полученные в MATLAB и SIMULINK.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
- Решить следующие линейные дифференциальные уравнения:
а)
б)
- При каком значении а и при каких начальных условиях решение уравнения
имеет вид:
- В чем заключается метод понижения производной? Пользуясь этим методом, составить схемы моделирования для всех вариантов п.1.
- Используя метод понижения производной, составить схемы моделирования следующих дифференциальных уравнений:
а) 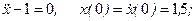
в)
г)
- Схема моделирования представляет собой кольцо из трех интеграторов с единичными коэффициентами и одинаковыми начальными условиями. Найти моделируемое дифференциальное уравнение и его аналитическое решение.
- Как изменятся графики решения линейного однородного дифференциального уравнения при замене знаков всех начальных условий на противоположные?
- Описать процедуру перехода от системы дифференциальных уравнений к одному уравнению и обратную процедуру, рассмотрев случай n=3. Привести пример.
- Составить схему моделирования и найти решение системы линейных дифференциальных уравнений
если матрица A имеет вид
ВАРИАНТЫ ЗАДАНИЙ ПО РАБОТЕ № 2
| № | ||||||||||||
| a1 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,6 |
| a0 | 0,4 | 1,6 | 4,8 | 0,5 | 1,8 | 5,0 | 0,6 | 2,0 | 5,4 | 0,7 | 2,2 | 5,8 |
| a11 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -0,9 | -0,9 | -0,9 | -0,9 | -0,9 |
| a12 | 1,0 | 0,8 | 0,7 | 0,6 | 0,57 | 0,4 | 0.35 | 1,0 | 0,8 | 0,7 | 0,6 | 0,5 |
| a22 | -2,0 | -1,8 | -1,7 | -1,6 | -1,5 | -1,4 | -1,3 | -1,9 | -1,7 | -1,6 | -1,5 | -1,4 |
| № | ||||||||||||
| a1 a0 | 0,1 0,8 | 0,3 2,4 | 6,0 | 0,9 8,8 | 0,1 0,9 | 0,3 2,6 | 0,7 6,4 | 1.1 9,0 | 0,2 1,0 | 0,3 2,8 | 0,8 6,8 | 0,6 5,8 |
| a11 | -0,9 | -0,9 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,5 | -0,5 | -0,5 |
| a12 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 | 0,6 | 0.5 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 |
| a22 | -1,3 | -1,6 | -1,6 | -1,6 | -1,5 | -1,4 | -1,3 | -1,2 | -1,1 | -1,5 | -1,3 | -1,2 |
Ответы на контрольный вопрос 1а,б,в,г:
а. 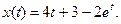
в.
г.
Моделирование динамических систем: численные методы решения ОДУ
Очень кратко рассмотрев основы механики в предыдущей статье, перейдем к практике, ибо даже той краткой теории что была рассмотрена хватит с головой.
Камень бросают вертикально, без начальной скорости с высоты h = 100 м. Пренебрегая сопротивлением воздуха, определить закон движения камня, как функцию высоты камня над поверхностью Земли от времени. Ускорение свободного падения принять равным 10 м/с 2
1. Формализация задачи
То, с чего начинается любое моделирование. Под формализацией понимают получение математических выражений, описывающих происходящий процесс. При этом формулируются допущения: перечень упрощений модели за счет факторов, влиянием которых можно пренебречь.
Для этой задачи применимо допущение, согласно которому камень можно считать материальной точкой. К этой точке приложена одна единственная сила — сила тяжести, так мы используем допущение об отсутствии сопротивления воздуха.
Следующим допущением будет полагать что Земля плоская, так как высота, с которой мы бросаем камень пренебрежимо мала в сравнении с размерами планеты, а значит кривизной её поверхности можно пренебречь. Тогда сила тяжести может считаться постоянной, направленной перпендикулярно поверхности Земли и равной по модулю
где g — ускорение свободного падения у поверхности Земли. Теперь пришло время составить уравнения движения камня. Помните эти уравнения
Левая их часть нас пока не интересует, а вот в правой стоят суммы проекций сил, приложенных к точке на оси координат. Пусть оси x и y располагаются на поверхности, а ось z направлена вверх перпендикулярно ей. Сила одна единственная, её проекции на оси x и y равны нулю, а на ось z проекция отрицательна, так как сила направлена против направления оси, то есть
Масса камня, очевидно не равна нулю, значит можно спокойно поделить обе части получившихся уравнений на неё
Не буду занудствовать, доказывая что движение камня будет происходить строго вертикально, хотя это нужно сделать с формальной точки зрения. Ноль в правой части первых двух уравнений совершенно не означает невозможность движения вдоль этих осей — вспоминаем первый закон Ньютона. На этом я остановлюсь в следующей статье более подробно, а пока справедливо положим одномерность движения, выписав окончательное дифференциальное уравнение
То что у нас получилось не много не мало — математическая модель процесса происходящего в задаче. Пафосно, да?
Нет. Анализируя это уравнение мы делаем вывод, например, что масса камня не оказывает влияния на закон его движения, ведь массы в этом уравнении нет. Видите, даже не решив уравнения, мы уже формально доказали справедливость опыта с пером и кусочком свинца в вакууме, который любят показывать в школе (а некоторые повторили его на Луне).
Аналитическое решение получить просто, даже не буду заморачиваться, оно такое
А вот как решить это численно? И что это вообще такое — «численно»?
2. Численное интегрирование дифференциального уравнения первого порядка
Какой такой первый порядок? Я же говорил в прошлый раз, что уравнения движения имеют второй порядок. Всё правильно, но большинство методов решения диффур на компьютере умеют решать только уравнения первого порядка. Есть методы прямого интегрирования уравнений второго порядка (например метод Верле), но о них не сейчас.
Во-первых, это уравнение относится к такому типу, что допускает понижение порядка. Правая часть не зависит от неизвестной функции (там нет z), поэтому вспоминаем, что
проекция ускорения на ось z равна первой производной проекции скорости на ту же оcь z. Ну классно, тогда
вот вам и уравнение первого порядка. Не всегда этот номер проходит (не буду я сейчас про форму Коши!), но в данном случае всё в порядке. Будем искать не координату а скорость точки. Что дальше-то? А дальше
ведь производная, мы же знаем, это отношение бесконечно малого приращения функции (скорости) в к вызвавшему его бесконечно малому приращению аргумента (время). Возьмем очень маленький промежуток времени , настолько небольшой что можно считать
Что получается? А вот что
Мы получили приращение скорости. Отрицательное приращение. Как это так, камень, падая вниз будет разгонятся же! Да, будет. Его скорость, вектор его скорости, будет направлен вниз. А значит проекция этого вектора на ось z будет отрицательной. Всё правильно, мы получаем растущую по абсолютному значению проекцию вектора, направленного вниз. Мы знаем, начальное значение скорости — ноль, а значит
Пользуясь тем что мы можем вычислить приращение скорости, посчитаем, какова будет скорость скажем через 0.1 секунды
а ещё через 0.1 секунды
и ещё через 0.1 секунды
Хм, так мы можем продолжать довольно долго, но ограничимся промежутком времени в одну секунду
| Время, с | Скорость, м/с |
| 0.0 | 0.0 |
| 0.1 | -1.0 |
| 0.2 | -2.0 |
| 0.3 | -3.0 |
| 0.4 | -4.0 |
| 0.5 | -5.0 |
| 0.6 | -6.0 |
| 0.7 | -7.0 |
| 0.8 | -8.0 |
| 0.9 | -9.0 |
| 1.0 | -10.0 |
То есть, воспользовавшись формулой
мы получили зависимость скорости точки от времени. А всего-то нужно взять значение скорости в текущий момент времени, и добавить к нему приращение, которое скорость получит в новый момент времени, отстоящий от текущего на секунд. Приращение времени называется здесь шагом интегрирования. А приращение мы вычисляем как значение производной искомой функции в текущий момент времени умноженное на шаг. Просто? Да просто конечно. И та формула, которую я написал, имеет название название — явный метод Эйлера для численного решения дифференциальных уравнений. Это так называемая рекуррентная формула, когда новое значение вычисляемой величины зависит от её предыдущего значения.
А что же с высотой точки над Землей? Да всё аналогично, смотрите
ведь проекция скорости есть производная от соответствующей координаты. Применим формулу метода Эйлера для этого уравнения, ведь скорость мы уже знаем
и по этой формуле добавим в нашу таблицу ещё одну колонку
| Время, с | Скорость, м/с | Высота, м |
| 0.0 | 0.0 | 100.0 |
| 0.1 | -1.0 | 100.0 |
| 0.2 | -2.0 | 99.9 |
| 0.3 | -3.0 | 99.7 |
| 0.4 | -4.0 | 99.4 |
| 0.5 | -5.0 | 99.0 |
| 0.6 | -6.0 | 98.5 |
| 0.7 | -7.0 | 97.9 |
| 0.8 | -8.0 | 97.2 |
| 0.9 | -9.0 | 96.4 |
| 1.0 | -10.0 | 95.5 |
Хм, ну, во-первых, заметно, что высота меняется у нас уже неравномерно, так как скорость со временем меняется. Теперь наша производная сама зависит от времени. Но уже на первом шаге, мы замечаем неладное — скорость уже есть, а вот высота по прежнему 100 метров. Как так?
Это вышло потому, что на каждом шаге мы полагаем производную (скорость) постоянной. Метод не дает информации о том, что происходит с решением между шагами. Соответственно накапливается погрешность, сравним полученное решение с точным
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 100.0 | 99.95 |
| 0.2 | -2.0 | 99.9 | 99.80 |
| 0.3 | -3.0 | 99.7 | 99.55 |
| 0.4 | -4.0 | 99.4 | 99.20 |
| 0.5 | -5.0 | 99.0 | 98.75 |
| 0.6 | -6.0 | 98.5 | 98.20 |
| 0.7 | -7.0 | 97.9 | 97.55 |
| 0.8 | -8.0 | 97.2 | 96.80 |
| 0.9 | -9.0 | 96.4 | 95.95 |
| 1.0 | -10.0 | 95.5 | 95.00 |
Да, наш камень как будто зависает в воздухе. Численное решение отстает от аналитического, и чем дальше мы считаем, тем выше погрешность счета. Погрешность накапливается, так как на каждом шаге мы берем всё более и более грубое приближение. Что делать?
Во первых, можно уменьшить шаг. Скажем в 10 раз, пусть секунды
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.96 | 99.95 |
| 0.2 | -2.0 | 99.81 | 99.80 |
| 0.3 | -3.0 | 99.57 | 99.55 |
| 0.4 | -4.0 | 99.22 | 99.20 |
| 0.5 | -5.0 | 98.78 | 98.75 |
| 0.6 | -6.0 | 98.23 | 98.20 |
| 0.7 | -7.0 | 97.59 | 97.55 |
| 0.8 | -8.0 | 96.84 | 96.80 |
| 0.9 | -9.0 | 96.00 | 95.95 |
| 1.0 | -10.0 | 95.05 | 95.00 |
Уже лучше, погрешность в конце счета не превышает 0,05 метров, и это в 10 раз меньше предыдущего значения. Можно предположить, что уменьшив шаг ещё в 10 раз мы получим ещё более точное решение. Я схитрил, выводя значения только для 10 точек с шагом 0.1, на самом деле, чтобы получить такую таблицу нужны уже 100 итерации а не 10. При шаге 0.001 потребуется уже тысяча итераций, а результат будет таким
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.9505 | 99.95 |
| 0.2 | -2.0 | 99.8010 | 99.80 |
| 0.3 | -3.0 | 99.5515 | 99.55 |
| 0.4 | -4.0 | 99.2020 | 99.20 |
| 0.5 | -5.0 | 98.7525 | 98.75 |
| 0.6 | -6.0 | 98.2030 | 98.20 |
| 0.7 | -7.0 | 97.5535 | 97.55 |
| 0.8 | -8.0 | 96.8040 | 96.80 |
| 0.9 | -9.0 | 95.9545 | 95.95 |
| 1.0 | -10.0 | 95.0050 | 95.00 |
Если вы попробовали выполнить эти расчеты в ручную, то понимаете теперь насколько они однообразны и трудоемки, если нужна высокая точность. Именно поэтому расцвет численного моделирования совпал с появлением компьютеров. Они как раз и нужны для того, чтобы быстро выполнять множество однообразных операций над числами.
Метод Эйлера самый простой из известных методов интегрирования дифференциальных уравнений. Из нашего простого примера видно, что погрешность метода прямо пропорциональна шагу интегрирования, и это действительно так. Такие методы называются методами 1-го порядка точности.
Точность расчетов даже на шаге 0.1 можно улучшить, если мы применим, скажем метод Рунге-Кутты 4-го порядка точности. Но это отдельная история.
Заключение
Задумайтесь… Мы рассмотрели очень простой пример. Мы даже не применяли компьютер, но уже понимаем принцип, по которому работают те самые мощные в мире суперкомпьютеры, что моделируют ранние этапы жизни Вселенной. Конечно, там всё устроено гораздо сложнее, но принцип лежит этот же самый.
Представьте себе, какой мощный инструмент вы получаете в свои руки. Эта последняя статья, где мы не будем применять компьютер. Я обещал Octave. В следующий раз будет именно он.
http://life-prog.ru/2_14909_modelirovanie-differentsialnih-uravneniy.html
http://habr.com/ru/post/349162/

























































































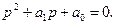
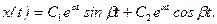
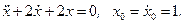
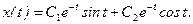
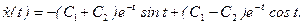
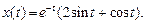
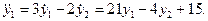
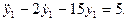
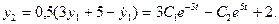
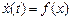 , сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.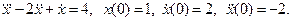
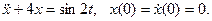
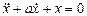 имеет вид:
имеет вид: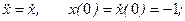
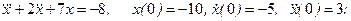
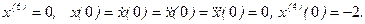
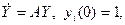 если матрица A имеет вид
если матрица A имеет вид