Модифицированный метод Ньютона
Теорема 6. Пусть на [a,b] задана дважды дифференцируемая функция f(x), причем выполнены след. условия
а) f(a)f(b) 0
можно вычислить модифицированным методом Ньютона единственный корень ξ с любой степенью точности.
Доказательство: Пусть f’(x)>0, f’’(x0)>0 (см.рис.3) Тогда в качестве x0 берем точку x0=b, так как f(b)f’’(b)>0. Из (3.23) следует, что xn+1 x1>…>xn>a (3.24)
Покажем теперь, что эта последовательность имеет предел ξ. Пусть xn-1> ξ. Докажем, что xn> ξ. Для этого запишем n-ое приближение, полученное по формуле Ньютона (см. формулу (3.17)) и по модифицированной формуле Ньютона (3.23)
и найдем разность 
Из теории выпуклых функций известно, что если f’’(x) и сохраняет знак на [a,b], то f(x)является выпуклой. Для выпуклой функции f(x) производная f’(x) является неубывающей, то есть для 


С учетом (3.26) из (11) следует 


ξ≤xn. (3.27)
Таким образом, из (3.24) и (3.27) получили убывающую сходящуюся последовательность
x0>x1>…>xn≥ξ.
Следовательно, для любого сколь угодно малого ε>0 можно указать такое n, что
|xn-ξ|
Модификации метода ньютона решения нелинейных уравнений
нПДЙЖЙЛБГЙЙ НЕФПДБ оШАФПОБ.
нЕФПД УЕЛХЭЙИ ДМС ОЕМЙОЕКОПЗП ХТБЧОЕОЙС.
НЕФПДБ оШАФПОБ ФТЕВХЕФУС ЧЩЮЙУМСФШ РТПЙЪЧПДОХА ЖХОЛГЙЙ f(x), ЮФП ОЕ ЧУЕЗДБ ХДПВОП, Б ЙОПЗДБ РТБЛФЙЮЕУЛЙ ОЕЧПЪНПЦОП. ч НЕФПДЕ УЕЛХЭЙИ РТПЙЪЧПДОБС f ‘(x (k) ) ЪБНЕОСЕФУС ОБ ДТПВШ (ФБЛ ОБЪЩЧБЕНХА ТБЪДЕМЕООХА ТБЪОПУФШ) (f(x (k) ) — f(x (k-1) )) / (x (k) — x (k-1) ).
ч ТЕЪХМШФБФЕ ЖПТНХМБ НЕФПДБ РТЙОЙНБЕФ ЧЙД:
| x (k+1) = x (k) — f(x (k) )(x (k) — x (k-1) ) / (f(x (k) ) — f(x (k-1) )), k = 1, 2, . | (2.19) |
|---|
ЗДЕ x (0) ,x (1) — ОЕЛПФПТЩЕ ОБЮБМШОЩЕ РТЙВМЙЦЕОЙС Л ЛПТОА.
зЕПНЕФТЙЮЕУЛЙК УНЩУМ НЕФПДБ УЕЛХЭЙИ ЪБЛМАЮБЕФУС Ч ЪБНЕОЕ ОБ ЙФЕТБГЙЙ У ОПНЕТПН k ЗТБЖЙЛБ ЖХОЛГЙЙ y=f(И) ОБ УЕЛХЭХА, РТПИПДСЭХА ЮЕТЕЪ ФПЮЛЙ (x (k) ,f(x (k) )) Й (x (k-1) ,f(x (k-1) )) Й, УМЕДПЧБФЕМШОП, ЪБДБЧБЕНХА ХТБЧОЕОЙЕН
дБМЕЕ ОБИПДЙН ФПЮЛХ ЕЕ РЕТЕУЕЮЕОЙС У ПУША OX, ЮФП УППФЧЕФУФЧХЕФ ТЕЫЕОЙА МЙОЕКОПЗП ХТБЧОЕОЙС:
1) ч ПВЭЕН УМХЮБЕ УИПДЙНПУФШ РП НЕФПДХ оШАФПОБ РТПЙУИПДЙФ ВЩУФТЕЕ, ЮЕН РП НЕФПДХ УЕЛХЭЙИ, Й ЛТПНЕ ФПЗП ОЕ ФТЕВХЕФУС ОБИПЦДЕОЙС УТБЪХ ДЧХИ ОБЮБМШОЩИ РТЙВМЙЦЕОЙК Л ЙУЛПНПНХ ЛПТОА. оП РТЙ ЙУРПМШЪПЧБОЙЙ НЕФПДБ УЕЛХЭЙИ ОЕ ФТЕВХЕФУС ЧЩЮЙУМЕОЙС РТПЙЪЧПДОПК.
2) хУМПЧЙЕ ПЛПОЮБОЙС ЙФЕТБГЙК Ч НЕФПДЕ УЕЛХЭЙИ ПУФБЕФУС ФЕН ЦЕ, ЮФП Й Ч ЛМБУУЙЮЕУЛПН НЕФПДЕ оШАФПОБ: | x (k+1) — x (k) | ≤ ε.
нЕФПД ИПТД ДМС ОЕМЙОЕКОПЗП ХТБЧОЕОЙС.
ч НЕФПДЕ ИПТД РТПЙЪЧПДОБС f ‘(x (k) ) НЕФПДБ оШАФПОБ ЪБНЕОСЕФУС ОБ ЕЭЕ ВПМЕЕ РТПУФХА (РП УТБЧОЕОЙА У НЕФПДПН УЕЛХЭЙИ) ТБЪДЕМЕООХА ТБЪОПУФШ (f(x (k) ) — f(x (0) )) / (x (k) — x (0) )
ч ТЕЪХМШФБФЕ ЖПТНХМБ НЕФПДБ ИПТД РТЙОЙНБЕФ ЧЙД:
| x (k+1) = x (k) — f(x (k) )(x (k) — x (0) ) / (f(x (k) ) — f(x (0) )), k = 1, 2, . | (2.20) |
|---|
РТЙЮЕН x (0) , x (1) — ОЕЛПФПТЩЕ ОБЮБМШОЩЕ РТЙВМЙЦЕОЙС Л ЛПТОА. зЕПНЕФТЙЮЕУЛЙ ТБУУНБФТЙЧБЕНЩК НЕФПД ПЪОБЮБЕФ ЪБНЕОХ ОБ ЛБЦДПК ЙФЕТБГЙЙ ЗТБЖЙЛБ ЖХОЛГЙЙ y=f(И) ОБ ИПТДХ, ФП ЕУФШ ЮЕТЕЪ ФПЮЛЙ (x (0) ,f(x (0) )) Й (x (k) ,f(x (k) )) РТПЧПДЙН ИПТДХ
Й ОБИПДЙН ФПЮЛХ ЕЕ РЕТЕУЕЮЕОЙС У ПУША OX, ЮФП УППФЧЕФУФЧХЕФ ТЕЫЕОЙА МЙОЕКОПЗП ХТБЧОЕОЙС:
чЩТБЦБС ПФУАДБ x, РПМХЮБЕН:
ъбнеюбойе 2.6 лТЙФЕТЙК ПЛПОЮБОЙС ЙФЕТБГЙК Ч НЕФПДЕ ИПТД ЙНЕЕФ ЧЙД:
хРТПЭЕООЩК НЕФПД оШАФПОБ.
ьФПФ НЕФПД ЙНЕЕФ ЧЙД
| x (k+1) = x (k) — f(x (k) )/f ‘(x (0) ) , k = 0, 1, 2, . | (2.21) |
|---|
ЗДЕ x (0) — ОЕЛПФПТПЕ ОБЮБМШОПЕ РТЙВМЙЦЕОЙЕ Л ЛПТОА.
лТЙФЕТЙК ПЛПОЮБОЙС ДБООПЗП ЙФЕТБГЙПООПЗП РТПГЕУУБ ЙНЕЕФ ЧЙД:
л ДПУФПЙОУФЧБН ЬФПЗП НЕФПДБ УМЕДХЕФ ПФОЕУФЙ РТПУФПФХ ЕЗП ТЕБМЙЪБГЙЙ Й ЧПЪНПЦОПУФШ ПВПВЭЕОЙС ОБ УЙУФЕНЩ ХТБЧОЕОЙК (УН. УМЕДХАЭЙК РБТБЗТБЖ), Б Л ОЕДПУФБФЛБН — ВПМЕЕ НЕДМЕООХА РП УТБЧОЕОЙА У НЕФПДПН оШАФПОБ УИПДЙНПУФШ.
нПДЙЖЙЛБГЙС НЕФПДБ оШАФПОБ ДМС УЙУФЕНЩ ДЧХИ ХТБЧОЕОЙК.
дМС ТЕЫЕОЙС УЙУФЕНЩ ЙЪ ДЧХИ ХТБЧОЕОЙК
ЙУРПМШЪХЕФУС УМЕДХАЭБС НПДЙЖЙЛБГЙС НЕФПДБ оШАФПОБ:
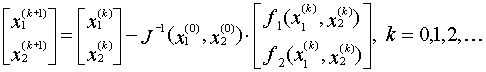 | (2.22) |
|---|
ъбнеюбойе 2.7 1) ч ДБООПН НЕФПДЕ Ч ПФМЙЮЙЕ ПФ ЛМБУУЙЮЕУЛПЗП НЕФПДБ оШАФПОБ ПВТБФОХА НБФТЙГХ ФТЕВХЕФУС РПДУЮЙФЩЧБФШ ФПМШЛП ПДЙО ТБЪ.
2) хУМПЧЙЕ ПЛПОЮБОЙС ЙФЕТБГЙПООПЗП РТПГЕУУБ ЙНЕЕФ ЧЙД: || x (k+1) — x (k) || ≤ ε
Численные методы решения нелинейных уравнений. Метод Ньютона для решения уравнений с одной переменной
Численные методы решения нелинейных уравнений. Метод Ньютона для решения уравнений с одной переменной
Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643-1727), под именем которого и обрёл свою известность.
Метод был описан Исааком Ньютоном в рукописи De analysi per aequationes numero terminorum infinitas ( лат .О б анализе уравнениями бесконечных рядов), адресованной в 1669 году Барроу , и в работе De metodis fluxionum et serierum infinitarum ( лат.Метод флюксий и бесконечные ряды) или Geometria analytica ( лат.Аналитическая геометрия) в собраниях трудов Ньютона, которая была написана в 1671 году. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения xn , а последовательность полиномов и в результате получал приближённое решение x.
Впервые метод был опубликован в трактате Алгебра Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе Analysis aequationum universalis (лат. Общий анализ уравнений). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений xn вместо более трудной для понимания последовательности полиномов, использованной Ньютоном.
Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.
В соответствии с данным методом задача поиска корня функции сводится к задаче поиска точки пересечения с осью абсцисс касательной, построенной к графику функции .
Рис.1 . График изменение функции
Проведенная в любой точке касательная линия к графику функции определяется производной данной функции в рассматриваемой точке, которая в свою очередь определяется тангенсом угла α ( ). Точка пересечения касательной с осью абсцисс определяется исходя из следующего соотношения в прямоугольном треугольнике: тангенс угла в прямоугольном треугольнике определяется отношением противолежащего катета к прилежащему катету треугольнику. Таким образом, на каждом шаге строится касательная к графику функции в точке очередного приближения . Точка пересечения касательной с осью Ox будет являться следующей точкой приближения . В соответствии с рассматриваемым методом расчет приближенного значения корня на i -итерации производится по формуле:
Наклон прямой подстраивается на каждом шаге наилучшим образом, однако следует обратить внимание на то, что алгоритм не учитывает кривизну графика и следовательно в процессе расчета остается неизвестно в какую сторону может отклониться график.
Условием окончания итерационного процесса является выполнение следующего условия:
где ˗ допустимая погрешность определения корня.
Метод обладает квадратичной сходимостью. Квадратичная скорость сходимость означает, что число верных знаков в приближённом значении удваивается с каждой итерацией.
Математическое обоснование
Пусть дана вещественная функция , которая определена и непрерывна на рассматриваемом участке. Необходимо найти вещественный корень рассматриваемой функции.
Вывод уравнения основано на методе простых итераций, в соответствии с которым уравнение приводят к эквивалентному уравнению при любой функции . Введем понятие сжимающего отображения, которое определяется соотношением .
Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Данное требование означает, что корень функции должен соответствовать экстремуму функции .
Производная сжимающего отображения определяется в следующем виде:
Выразим из данного выражение переменную при условии принятого ранее утверждения о том, что при необходимо обеспечить условие . В результате получим выражение для определения переменной :
С учетом этого сжимающая функция прием следующий вид:
Таким образом, алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
Алгоритм нахождения корня нелинейного уравнения по методу Ньютона для уравнения с одной переменной
1. Задать начальную точку приближенного значения корня функции , а также погрешность расчета (малое положительное число ) и начальный шаг итерации ( ).
2. Выполнить расчет приближенного значения корня функции в соответствии с формулой:
3. Проверяем приближенное значение корня на предмет заданной точности, в случае:
— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается.
— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.
Пример решения уравнений
по методу Ньютона для уравнения с одной переменной
В качестве примера, рассмотрим решение нелинейного уравнения методом Ньютона для уравнения с одной переменной . Корень необходимо найти с точностью в качестве первого приближения .
Вариант решения нелинейного уравнения в программном комплексе MathCAD представлен на рисунке 3.
Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.2).
Рис.2 . Результаты расчета по методу Ньютона для уравнения с одной переменной
Для обеспечения заданной точности при поиске приближенного значения корня уравнения в диапазоне необходимо выполнить 4 итерации. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .
Рис.3 . Листинг программы в MathCad
Модификации метода Ньютона для уравнения с одной переменной
Существует несколько модификаций метода Ньютона, которые направлены на упрощение вычислительного процесса.
Упрощенный метод Ньютона
В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что ведет к увеличению вычислительных затрат. Для уменьшения затрат, связанных с вычислением производной на каждом шаге расчета, можно произвести замену производной f’( xn ) в точке xn в формуле на производную f’(x0) в точке x0. В соответствии с данным методом расчета приближенное значение корня определяется по следующей формуле:
Таким образом, на каждом шаге расчета строятся прямые , которые параллельны касательной к кривой y=f(x) в точке B0 (см. рис.4). Преимуществом данного метода является то, что производная функции вычисляется один раз.
Разностный метод Ньютона
В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что не всегда удобно, а иногда практически невозможно. Данный способ позволяет производную функции заменить разностным отношением (приближенным значением):
В результате приближенное значение корня функции f(x) будет определяться выражением разностного метода Ньютона:
Двух шаговый метод Ньютона
В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что не всегда удобно, а иногда практически невозможно. Данный способ позволяет производную функции заменить разностным отношением (приближенным значением):
В результате приближенное значение корня функции f(x) будет определяться следующим выражением:
Метод секущих является двух шаговым, то есть новое приближение определяется двумя предыдущими итерациями и . В методе необходимо задавать два начальных приближения и . Скорость сходимости метода будет линейной.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
http://e-lib.gasu.ru/eposobia/metody/R_2_4.html
http://simenergy.ru/math-analysis/solution-methods/45-method-newton-s