Решение уравнений с помощью монотонности функций
Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).
Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.
1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).
2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.
Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.
Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.
Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.
Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:
то уравнение имеет единственный корень или не имеет корней.
Разумеется, количество слагаемых может быть больше двух.
Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):
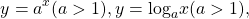
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:
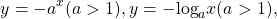
Примеры решения уравнений с помощью использования монотонности функций.
Перепишем уравнение в виде
является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
На промежутке (-∞;0) функция
— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.
Аналогично, на промежутке (0:∞)
— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.
В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.
2 комментария
Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям
Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.
Урок на тему: «Использование монотонности функций при решении уравнений и неравенств» (11 кл.)
Урок на тему: «Использование монотонности функций при решении уравнений и неравенств» (11 кл.)
Всё чаще и чаще «линия уравнений» в школьном курсе математики пересекается с «функциональной линией». В задачниках, в материалах ЕГЭ, в задачах, представленных на вступительных экзаменах в ВУЗы, предлагаются нестандартные уравнения, при решении которых необходимо использовать свойства функций. Владение данный приёмом позволяет более полно оценить уровень знаний ученика, степень его математической подготовки, математической культуры. Большое внимание использованию свойств функций при решение уравнений и неравенств уделено в учебнике под ред. Мордковича и начала анализа. 10 кл. (профильный уровень). Уже в теме «Свойства функций» показано применение монотонности функций, ограниченности при решении уравнений и неравенств (№ 8.29 – 8.35; № 8.51 – 8.52.). Неоднократное обращение авторами учебника к использованию этого приёма при решении тригонометрических уравнений и неравенств (№ 22.57;22.58; 23.35), при исследовании функции с помощью производной (№ 44.69 – 44.71; 44.75 – 44.76; 45.15; 46.39 – 46.40) подчёркивает важность усвоения данного материала учащимися. Но всё же такое «размазанное» расположение задач несколько мешает более полному усвоению приёма применения свойств функций при решении уравнений и неравенств, поэтому необходимо отвести цикл уроков для обобщения этого приёма. Это вполне можно осуществить на занятиях спецкурса по подготовки к ЕГЭ.
Основная цель изучения темы «Использование свойств функций при решении уравнений и неравенств» – научить учеников применять свои умения в нестандартных ситуациях.
К задачам, поставленным перед учениками в процессе изучения данной темы, следует отнести:
— систематизация знаний перед сдачей Единого Государственного Экзамена (ведь именно в частях В и С предлагаются сложные уравнения и неравенства, решение которых можно значительно упростить, применив свойства функции);
— приобретение необходимого набора умений по решению уравнений и неравенств, тем самым лучше подготовиться к обучению в ВУЗе, где математика является профилирующим предметом;
— изучение основных типов уравнений и неравенств, в которых возможно использование свойств функции;
— повторение свойств функций, упрощающих решение уравнений и неравенств.
Вашему вниманию будет предложен урок на тему «Использование монотонности функций при решении уравнений и неравенств». Эта тема рассчитана на 3 часа. Будет представлен второй урок из этой темы. На первом уроке учащиеся повторили определение, свойства, достаточные условия монотонности функций. Ранее были составлены таблицы «Свойства монотонных функций» (табл. 1) и «Банк монотонных функций» (табл. 2).
К основному содержанию первого урока необходимо отнести теорему, устанавливающую связь монотонности функций, входящих в уравнение, с количеством корней соответствующего уравнения.
Второй урок посвящён особому типу уравнений и неравенств, при решении которых используется монотонность функций. На этом уроке будет сформулирован и отработан алгоритм решения уравнений и неравенств такого типа. А также разработана техника составления подобных уравнений и неравенств. В конце урока предложена небольшая творческая работа. Домашнее задание имеет три уровня сложности. В него входят различные этапы доказательства теоремы, уравнения и неравенства, решаемые изученным методом, а также творческая работа по составлению уравнений и неравенств. На уроке предполагается использование презентации по изучаемой теме.
Третий урок должен быть посвящён систематизации и закреплению приёмов решения уравнений и неравенств, изученных на первых двух уроках. После изучения данной темы
учащиеся должны знать:
· определения возрастающей, убывающей, монотонной функций;
· теорему, устанавливающую связь монотонности функций, входящих в уравнение, с количеством корней соответствующего уравнения;
· теоремы о равносильностях для монотонных функций;
· обобщённый алгоритм решения уравнений с использованием монотонности функций;
· виды уравнений и неравенств, решаемых с использованием монотонности функций.
Учащиеся должны уметь:
· находить область определения функций;
· исследовать функцию на монотонность;
· применять алгоритм решения уравнений с использованием монотонности функции к соответствующим видам уравнений. Рассмотрим краткое содержание урока на тему:
«Использование монотонности функций при решении уравнений и неравенств»
1. Проверка домашнего задания.
2. Постановка задачи.
3. Доказательство основной теоремы.
4. Применение теоремы при решении уравнений и неравенств. Формулировка алгоритма.
5. Отработка алгоритма при решении уравнений и неравенств.
6. Формулировка алгоритма, используемого при составлении задач, решаемых изученным методом.
7. Творческая работа.
После проверки домашнего задания ученикам предлагается решить следующее уравнение:

Данное уравнение нельзя решить ранее изученными методами. Ученики обращают внимание на то, что если перенести в правую часть второе слагаемое, обе части будут похожи наличием скобок, корня. Если же под корнем левой части выделить полный квадрат, то части будут иметь вид функции 
На экране появляется формулировка теоремы.
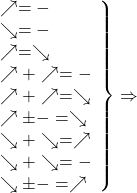
Теорема. Пусть область существования функций f(x) есть М.
Тогда
А) Если 
В) Если 
С) Если 
Учитель вместе с учениками доказывает первую часть теоремы. Доказательство записывается в тетрадь. Затем ученикам предлагается решить задания 1 и 2.
Задание 1. Пусть функция  определена на интервале
определена на интервале  и возрастает на нём. Решите уравнение
и возрастает на нём. Решите уравнение

Задание 2. Пусть функция 


На экране появляется задание 3, решение которого ученики разбирают вместе с учителем.
Задание 3. Решить уравнение
Рассмотрим функцию 
Тогда уравнение можно записать в виде
Исследуем функцию 
Область определения
Функция возрастает, как сумма возрастающих функций.
По теореме имеем:
Учитель предлагает сформулировать алгоритм решения подобных уравнений и неравенств. После предложенной детьми формулировки алгоритм появляется на экране.
1. Ввести функцию 


2. Исследовать функцию 
А) область определения
Б) характер монотонности.
3. Применив теорему, получить систему уравнений и неравенств.
4. Решить полученную систему. Записать ответ.
Ученикам предлагается, используя алгоритм, решить следующие уравнения и неравенства.
Решите уравнения и неравенства:
1. 
2. 
3. 
4. 
После решения предложенных уравнений и неравенств учитель задаёт ученикам вопрос: «Как придумать уравнение или неравенство, решаемое этим методом?» Ученики формулируют алгоритм:
1. Выбрать функции 

2. Ввести монотонную функцию 
3. Записать уравнение (неравенство) в виде


Учитель предлагает применить алгоритм к предложенным функциям:


Используя таблицы 1 и 2, ученики вводят монотонную функцию

Она возрастает, как сумма возрастающих функций.
Составим неравенство вида 

Теперь решим это неравенство.
Учителем предлагается небольшая самостоятельная работа: «Составить и решить изученным методом своё уравнение или неравенство для функций 

Дифференцированное домашнее задание предполагает три уровня сложности.
Решите уравнения и неравенства:
1. 
2. 
3. 
Придумайте и решите уравнение и неравенство, решаемые с помощью монотонности функции, если 

Докажите теорему, часть С.
Решите уравнения и неравенства:
1. 
2. 
3. 
Придумайте и решите уравнение и неравенство, решаемые с помощью монотонности функции.
Докажите теорему, часть А.
Решите уравнения и неравенства:
1. 
2. 
3. 
Придумайте и решите уравнение и неравенство, решаемые с помощью монотонности функции.
В процессе урока предполагается использование следующего раздаточного материала, который ученики вклеивают в справочник по математике.
Использование монотонности функций при решении
уравнений и неравенств
Теорема. Пусть область существования функций f(x) есть М.
Тогда
А) Если 
В) Если 
С) Если 
Пример применения теоремы.
Рассмотрим функцию
Тогда уравнение можно записать в виде
Исследуем функцию 
Область определения
Функция возрастает, как сумма возрастающих функций.
1. Ввести функцию 
2. 

3. Исследовать функцию 
i. А) область определения
ii. Б) характер монотонности.
4. Применив теорему, получить систему уравнений и неравенств.
5. Решить полученную систему. Записать ответ.
Как придумать уравнение или неравенство, решаемое этим методом?
1. Выбрать функции 

2. Ввести монотонную функцию 
3. Записать уравнение (неравенство) в виде


Пример применения алгоритма
Пусть 

Введём функцию 
Она возрастает, как сумма возрастающих функций.
Составим неравенство вида 

Свойства монотонности функций

Возрастающие






1. Алгебра и начала анализа. 10 кл. В 2 ч. Ч.2. задачник для общеобразовательных учреждений (профильный уровень) / под ред. . – 2-е изд., стер. – М.: Мнемозина, 2006. – 340 с.: ил.
2. Алгебра и начала анализа: Учеб. Для 11 кл. общеобразовательных учреждений / , , . – 2-е изд. – М.: Просвещение, 2003. – 448 с.: ил. – ISBN -0.
Использование монотонности при решении уравнений
презентация к уроку по алгебре (11 класс) по теме
Презентация к уроку в 11 классе (подготовка к ЕГЭ)
Скачать:
| Вложение | Размер |
|---|---|
| tema_uroka.ppt | 203.5 КБ |
Предварительный просмотр:
Подписи к слайдам:
Тема урока: Использование монотонности при решении уравнений Учитель математики Грязнова Е.В.
Задача: Решить уравнение
Билет №1 Решить уравнение . Решить уравнение .
Билет № 2 При каком условии логарифмическая функция возрастает? Какие из перечисленных функций являются возрастающими?
Билет № 3 При каком условии показательная функция убывает? Какие из перечисленных функций являются убывающими?
Билет № 4 Закончите предложение: Для возрастающей функции большему аргументу соответствует … . Закончите предложение: Сумма двух убывающих функций является … .
Билет № 5 Решите уравнение . Решите уравнение .
Если для любых двух значений аргумента x 1 и x 2 из некоторого промежутка из условия x 2 > x 1 следует f ( x 2 ) > f ( x 1 ) , то функция f (x ) называется возрастающей на этом промежутке; если для любых двух значений аргумента x 1 и x 2 из некоторого промежутка из условия x 2 > x 1 следует f (x 2 ) Мне нравится
http://pandia.ru/text/79/053/59736.php
http://nsportal.ru/shkola/algebra/library/2014/01/06/ispolzovanie-monotonnosti-pri-reshenii-uravneniy
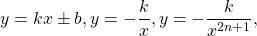
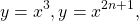
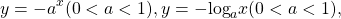
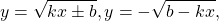
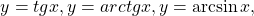
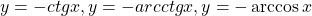
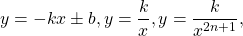
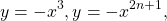
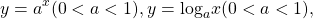
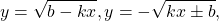
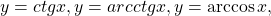
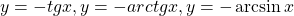
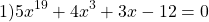
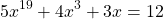
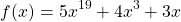
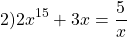
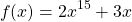
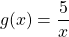




 и возрастает на нём. Решите уравнение
и возрастает на нём. Решите уравнение











































