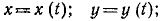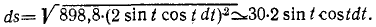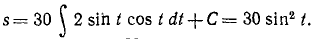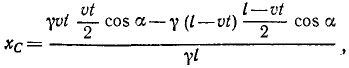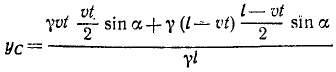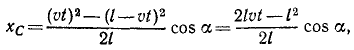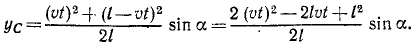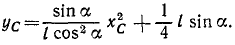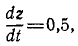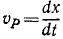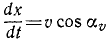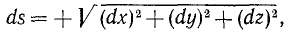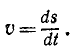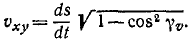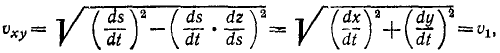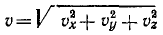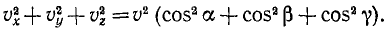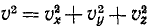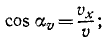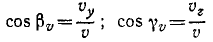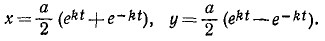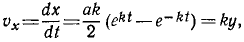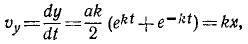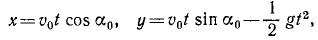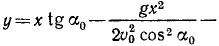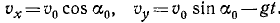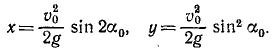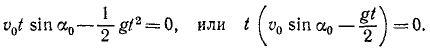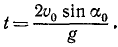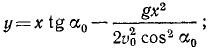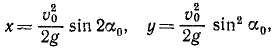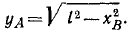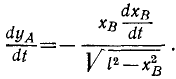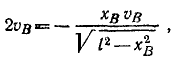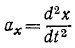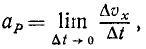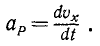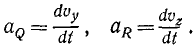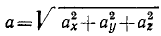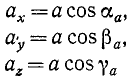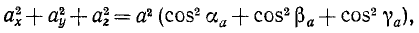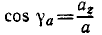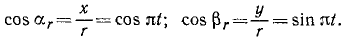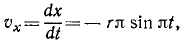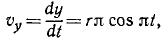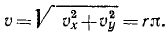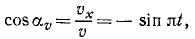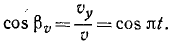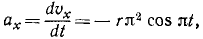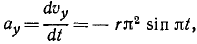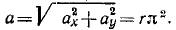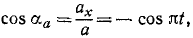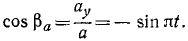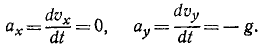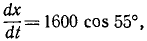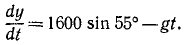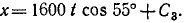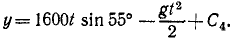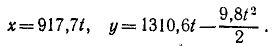Мостовой кран движется вдоль мастерской согласно уравнению

Тема 6. Общие сведения о движении. Прямолинейное движение точки

I: 159.

S:Рисунок воспроизводит со стробоскопической фотографии несколько положений работающего подъёмного крана. Будет ли поступательным движение 1) стрелы? 2) ковша?

+: 1) не будет; 2) будет

I: 160.

S:В каких случаях (см. рис.: а, б, в) движение спичечного коробка можно назвать поступательным?

+: б), в)

I: 161.

S:Можно ли принять Землю за материальную точку при расчёте: а) расстояния от Земли до Солнца; б) пути, пройденного Землёй по орбите вокруг Солнца за месяц; в) длины экватора; г) скорости движения точки экватора при суточном вращении Земли вокруг оси; д) скорости движения Земли по орбите вокруг Солнца?

+: а, б, д – можно; в, г – нельзя

I: 162.

S:Указать, в каких из приведённых ниже примерах изучаемое тело можно принять за материальную точку: а) вычисляют давление трактора на грунт; б) определяют высоту поднятия метеорологической ракеты; в) рассчитывают работу, совершённую при поднятии в горизонтальном положении плиты перекрытия известной массы на заданную высоту; г) определяют объём стального шарика, пользуясь мензуркой.

+: в случаях б и в

I: 163.

S:На рис. показана траектория движения материальной точки из А в В. Найти координаты точки в начале и конце движения, проекции перемещения на оси координат, перемещение.

+:А (20 м, 20 м); В (60 м, – 10 м);

40 м; – 30 м; 50 м.

I: 164.

S:По заданным графикам (см. рис.) написать уравнения x = (t). Из уравнений и графиков найти координаты тел через 5 с., скорости их движения, время и место встречи тел I и III.

+:x₁ = 5; x₂ = 5 – t; x₃ = – 10 + 0,5ּt; 5 м; 0; – 7,5 м; 0; – 1 м/с; 0,5 м/с; 10 с; – 5 м.

I: 165.

S:Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 20 м/с? а = … (м/с 2 )

+: 0,5

I: 166.

S:Найти центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 72 км/час и при этом частота вращения колеса 8 с – 1 . а = …(м/с – 2 )

+: 1005

I: 167.

S:Поезд через 10 с после начала движения приобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равна 3 м/с? t = …(с).

+: 50

I: 168.

S:Движение материальной точки в данной системе отсчёта характеризуется уравнениями у = 1 + 2ּt, x = 2 + t. Найти уравнение траектории. Построить траекторию на плоскости хОу . Указать положение точки при t = 0, направление и скорость движения.

+:у = – 3 + 2ּx; x = 2 м; у = 1 м; (м/с)

Тема 7. Уравнения движения точки. Сложное движение точки

I: 169.

S: По заданным уравнениям движения точки найти уравнение её траектории, а также указать закон движения точки по траектории, отсчитывая расстояние от начального положения точки. x = aּcos 2 t , у = aּsin 2 t.

+:Отрезок прямой x + у – a = 0, причём 0 ≤ x ≤ a; s = aּ ּsin 2 t.

I: 170.

S:Даны уравнения движения материальной точки

x = v₀ּtּcos α, у = v₀ּtּsin α – ּgּ t 2 ,

где v₀ – начальная скорость матер. точки, α – угол между v₀и горизонтальной осью х, g – ускорение свободного падения.

Определить траекторию движения матер. точки.

+: Траектория – параболау = хּtg α –

I: 171.

S: Мостовой кран движется вдоль мастерской согласно уравнению x = t; по крану катится в поперечном направлении тележка согласно уравнению у = 1,5ּt (x и y – в метрах, t – в секундах). Цепь укорачивается со скоростью v = 0,5 м/с. Определить траекторию центра тяжести груза; в начальном положении центр тяжести груза находился в горизонтальной плоскости Оxу; ось Оz направлена вертикально вверх.

+:Траектория – прямая: у = 1,5ּx; z = 0,5ּx.

I: 172.

S:Два поезда идут навстречу друг другу со скоростями 36 км/час и 54 км/час. пассажир, находящийся в первом вагоне, замечает, что второй поезд проходит мимо него в течение 6 с. Какова длина второго поезда? l = …(метров).

+: 150

I: 173.

S:На рис. приведены графики I движения велосипедиста и II движения мотоциклиста в системе отсчёта, связанной с Землёй. Написать уравнение движения велосипедиста в системе отсчёта, связанной с мотоциклистом, и построить график его движения в этой системе.

+:x =400 – 10ּt

I: 174.

S:График зависимости от времени ускорения а(t) матер. точки имеет вид, представленный на рис.; начальная скорость точки равна нулю. Определить график зависимости от времени скорости точки.

Отметьте правильный ответ.

+: 1), -: 2), -: 3), -: 4), -: 5), -: 6)

I: 175.

S:Локомотив находился на расстоянии L = 400 м от светофора и имел скорость 72 км/час, когда началось торможение.

Определите расстояние L₁ локомотива относительно светофора через 1 минуту после начала торможения, если он двигался с отрицательным ускорением (торможение), равным по величине а = 0,5 м/с 2 . L₁= … (м).

+: 0

I: 176.

S:Камень падает в шахту без начальной скорости. Звук от удара камня о дно шахты слышен через 6,5 сек. от момента начала его падения. Скорость звука равна 330 м/с. Определить глубину h шахты. Ускорение свободного падения принять равным g = 9,8 м/с 2 . (Результат вычисления округлить до целого числа.) h… (м).

+: 175

I: 177.

S:Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра v_O (см. рис.). Вдоль хорды диска движется точка М с относительной скоростью v_r. Определить направление ускорения Кориолиса в данный момент времени.

Отметьте правильный ответ:

+: к точке О, -: к точке А, -: к точке В, -: к точке С

I: 178.

S: Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра v_O (см. рис.). Вдоль диаметра диска движется точка М с относительной скоростью v_r. Определить направление ускорения Кориолиса в данный момент времени.

Отметьте правильный ответ:

-: к точке О, -: к точке А, -: к точке В, +: к точке С

I: 179.

S:В кривошипно-кулисном механизме кривошип ОА = 10 см вращается с угловой скоростью ω = 6 с –1 .

Определить относительную скорость ползуна А (относительно кулисы KLM) в тот момент, когда угол φ = 45 о (результат вычисления округлить до первого знака после запятой включительно);

+: 42,4

I: 180.

S:В кривошипно-кулисном механизме кривошип ОА = 10 см вращается с угловой скоростью ω = 6 с –1 .

Определить скорость о кулисы KLM (v₁) в тот момент, когда угол φ = 30 о );

+: 30

I: 181.

S: На токарном станке обтачивается цилиндр диаметра 80 мм. Шпиндель делает 30 об/мин. Скорость продольной подачи постоянна и равна 0,2 мм/с. Определить скорость резца относительно обрабатываемого цилиндра.

V_отн = … (мм/с). (Результат вычисления округлить до целого числа.)

Теоретическая механика

Пензенский государственный педагогический университет

имени В. Г. Белинского

А. А. Марко, О. В. Фолимагина, Н. В. Кирпичева

руководство для самостоятельной работы

Печатается по решению редакционно-издательского совета Пензенского государственного педагогического университета имени В. Г. Белинского

Марко А. А. Теоретическая механика. Руководство для самостоятельной работы. / А. А. Марко, О. В. Фолимагина, Н. В. Кирпичева. – Пенза: ПГПУ, 2010. – 40 с.

Учебно-методическое пособие предназначено студентам физико-математического факультета. Пособие содержит подборку базовых задач курса классической механики, варианты самостоятельных работ. В пособие приведены алгоритмы решения задач, краткий анализ содержания задач для самостоятельного решения, а также требования к оформлению и защите самостоятельных работ.

Ó Пензенский государственный

имени В. Г. Белинского, 2010

Ó А. А. Марко, 2010

Ó О. В. Фолимагина, 2010

Ó Н. В. Кирпичева, 2010

Уважаемый студент, немногочисленные законы и теоремы, лежащие в основе теоретической механики, находят весьма разнообразные и обширные применения. Поэтому наибольшие затруднения у изучающих теоретическую механику вызывает приложение общих положений теории к решению конкретных задач.

Залогом успешного освоения курса теоретической механики станет Ваша систематическая работа по изучению основных понятий, законов и принципов теории, а также решение задач.

Первая часть пособия содержит 8 структурированных тем, содержащих перечень основных теоретических позиций темы, рекомендуемые алгоритмы решения задач данной тематики и подборку задач, наиболее ярко иллюстрирующих методы и приемы решения задач темы.

Во второй части приведено описание самостоятельных работ, решение которых позволит Вам сформировать навыки использования законов механики в конкретных задачах.

Тема 1. Траектория и законы движения материальной точки.

Вопросы: материальная точка, траектория, закон движения, пройденный путь, перемещение, система отсчета.

1. выбирается система неподвижных координат – прямоугольная, полярная или какая-нибудь иная; начало координат и та или иная система выбираются, исходя из условия задачи, так, чтобы дальнейшее решение было возможно более простым;

2. на основании условий задачи для избранной системы координат составляются законы движения;

3. имея законы движения точки, можно определить ее положение в любой момент времени, установить направление движения, найти траекторию, исключив из законов движения время.

1. По данным законам движения точки найти уравнения ее траектории в координатной форме и указать на рисунке положение точки в моменты времени

a)

b)

c)

d)

2. Движение точки задано уравнениями: причем ось горизонтальна, ось направлена по вертикали вверх, и величины постоянные. Найти: 1) траекторию точки,
2) координаты наивысшего ее положения.

3. Точка движется по винтовой линии: Определить уравнение движения точки в цилиндрических координатах.

4. Точка участвует одновременно в двух взаимно перпендикулярных затухающих колебаниях согласно уравнениям: . Определить уравнения движения в полярных координатах и найти траекторию точки.

5. По заданным законам движения точки в декартовых координатах: ; ; найти ее траекторию и законы движения в сферических координатах.

Тема 2. Кинематика материальной точки.

Вопросы: скорость материальной точки, ускорение материальной точки, проекции скорости и ускорения, тангенциальное и нормальное ускорения, кривизна траектории.

1. выбирается система неподвижных координат – прямоугольная, полярная или какая-нибудь иная; начало координат и та или иная система выбираются, исходя из условия задачи, так, чтобы дальнейшее решение было возможно более простым;

2. на основании условий задачи для избранной системы координат составляются законы движения;

3. имея законы движения точки, определить проекции скорости или ускорения, путем дифференцирования законов движения по времени;

4. определить модули скорости и ускорения, радиус кривизны траектории и т.д.

1. По данным уравнениям движения точки найти уравнения ее траектории в координатной форме и указать на рисунке направление движения

а)

b) ; c)

2. Мостовой кран движется вдоль мастерской согласно уравнению ; по крану катится в поперечном направлении тележка согласно уравнению ( и – в метрах,
– в секундах). Цепь укорачивается со скоростью . Определить траекторию центра тяжести груза; в начальном положении центр тяжести груза находился в горизонтальной плоскости ; ось направлена вертикально вверх (сделать чертеж).

3. Точка движется по винтовой линии: Определить уравнение движения точки в цилиндрических координатах.

4. Движение точки задано уравнениями: причем ось горизонтальна, ось направлена по вертикали вверх, и ­ величины постоянные. Найти: 1) траекторию точки,
2) координаты наивысшего ее положения, 3) проекции скорости на координатные оси в тот момент, когда точка находится на
оси .

5. Из орудия, ось которого образует угол с горизонтом, выпущен снаряд со скоростью . Предполагая, что снаряд имеет только ускорение силы тяжести , найти годограф скорости снаряда.

6. Точка участвует одновременно в двух взаимно перпендикулярных затухающих колебаниях согласно уравнениям: . Определить проекции скорости точки на оси декартовых и полярных координат и найти модуль скорости точки.

7. Поезд движется равнозамедленно по дуге окружности радиуса и проходит путь , имея начальную скорость и конечную . Определить полное ускорение поезда в начале и в конце дуги, а также время движения по этой дуге.

8. Найти величину ускорения, а также радиус кривизны траектории точки колеса, катящегося без скольжения по горизонтальной оси , если точка описывает циклоиду согласно уравнениям: ( и – в метрах, – в секундах). Определить значение радиуса кривизны при .

9. Найти касательное и нормальное ускорения точки, движение которой выражается уравнениями .

10. Точка движется по линии пересечения сферы и цилиндра . Уравнения движения точки в сферических координатах имеют вид: . Найти проекции и модуль скорости ускорения точки в сферических координатах.

Тема 3. Плоское движение твердого тела.

Вопросы: твердое тело, поступательное и вращательное движение, угловая скорость и угловое ускорение.

1. выбирается система неподвижных координат – прямоугольная, полярная или какая-нибудь иная; начало координат и та или иная система выбираются, исходя из условия задачи, так, чтобы дальнейшее решение было возможно более простым;

2. на основании условий задачи для избранной системы координат составляются законы движения;

3. имея законы движения точки, определить проекции скорости или ускорения, путем дифференцирования законов движения по времени;

4. определить модули скорости и ускорения, радиус кривизны траектории и т.д.

1. Вал радиуса см приводится во вращение гирей Р , привешенной к нему на нити. Движение гири выражается уравнением , где — расстояние гири от места исхода

нити с поверхности вала, выраженное в сантиметрах,
— время в секундах. Определить угловую скорость и угловое ускорение вала, а также полное ускорение точки на поверхности вала в момент . Решить задачу в общем виде, выразив ускорение точек обода колеса через пройденное гирей расстояние , радиус колеса и ускорение гири

2. Ведущий вал I фрикционной передачи вращается с угловой скоростью рад/с и на ходу передвигается (направление указано стрелкой) так, что расстояние меняется по закону см ( — в секундах).

Определить: 1) угловое ускорение вала II как функцию расстояния d ; 2) ускорение точки на ободе колеса B в момент, когда , даны радиусы фрикционных колес:
= 5 см, = 15 см.

3. Стержень АВ длины 0,5 м движется
в плоскости рисунка.

Скорость ( м/с) образует угол 45° с осью х , совмещенной со стержнем. Скорость точки B образует угол 60° с осью х. Найти модуль скорости точки B и угловую скорость стержня.

4. На рисунке изображен суммирующий механизм. Две параллельные рейки 1 и 2 движутся в одну сторону с

постоянными скоростями и . Между рейками зажат диск радиуса , катящийся по рейкам без скольжения. Показать, что скорость средней рейки 3, присоединенной к оси C диска, равна полусумме скоростей реек 1 и 2. Найти угловую скорость диска.

Тема 4. Сложное движение материальной точки.

Вопросы: Абсолютное, переносное и относительное движение, теоремы сложения скоростей и ускорений.

Алгоритм решения (определение скорости точки в относительном, переносном и абсолютном движениях):

1. разложить движение на составляющие, определив абсолютное, относительное и переносное движения;

2. выбрать две системы координат: абсолютную и подвижную;

3. мысленно остановив переносное движение, найти скорость относительного движения;

4. мысленно отвлекаясь от относительного движения, найти скорость переносного движения точки;

5. применив теорему сложения скоростей, определить искомую абсолютную скорость точки.

Алгоритм решения (определение ускорения точки в относительном, переносном и абсолютном движениях):

1. разложить движение на составляющие, определив абсолютное, относительное и переносное движения;

2. выбрать две системы координат: абсолютную и подвижную;

3. мысленно остановив переносное движение, найти скорость и ускорение точки в относительном движении;

4. мысленно отвлекаясь от относительного движения, найти угловую скорость переносного движения и ускорение точки в переносном движении;

5. найти кориолисово ускорение точки;

6. применив теорему сложения ускорений, определить искомое абсолютное ускорение точки.

1. Наклонная плоскость АВ, составляющая угол 45° с горизонтом, движется прямолинейно параллельно оси Ох с постоянным ускорением м/с 2 .

По этой плоскости спускается тело Р с постоянным относительным ускорением м/с 2 ; начальные скорости плоскости и тела равны нулю, начальное положение тела определяется координатами . Определить траекторию, скорость и ускорение абсолютного движения тела.

2. Найти скорости и ускорения точек гусеницы танка, движущегося без скольжения по прямолинейному участку пути со скоростью и ускорением ; радиусы колес танка равны ; скольжением гусеницы по ободу колес пренебречь.

2. Шарик Р движется со скоростью 1,2 м/с от А к В по хорде АВ диска, вращающегося вокруг оси, проходящей через его центр перпендикулярно плоскости диска.

Найти абсолютное ускорение шарика,

когда он находится на кратчайшем расстоянии от центра диска, равном 30 см. В этот момент угловая скорость диска равна 3 рад/с, угловое замедление равно 8 рад/с 2 . Решить задачу в предположении, что диск вращается вокруг диаметра, параллельного хорде. Решить при условии, что осью вращения диска является диаметр, перпендикулярный хорде.

Тема 5. Прямая задача динамики.

Вопросы: Основные законы динамики материальной точки (законы Ньютона), понятия силы, массы, инерциальной системы отсчета, принципы независимого действия сил, дальнодействия, причинности, дифференциальное уравнение движения, виды сил в механике.

1. изобразить на рисунке материальную точку в текущем положении и приложенные к ней активные силы;

2. применив закон освобождаемости от связей, изобразить соответствующие реакции связей;

3. выбрать инерциальную систему отсчета, если она не указана в условии задачи;

4. определить по заданному закону движения ускорение материальной точки и найти его проекции на выбранные оси координат;

5. составить дифференциальные уравнения движения материальной точки, соответствующие принятой системе отсчета;

6. из системы составленных уравнений определить искомые величины.

1. Горизонтальная платформа, на которой лежит груз массы 1,02 кг, опускается вертикально вниз с ускорением 4 м/с 2 . Найти силу давления, производимого грузом на платформу во время их совместного спуска.

2. Камень массы 0,3 кг, привязанный к нити длины 1 м, описывает окружность в вертикальной плоскости. Определить наименьшую угловую скорость камня, при которой произойдет разрыв нити, если сопротивление ее разрыву равно 9 Н.

3. В вагоне поезда, идущего сначала по прямолинейному пути, а затем по закругленному со скоростью 20 м/с, производится взвешивание некоторого груза на пружинных весах; весы в первом случая показывают
50 Н, а на закруглении 51 Н. Определите радиус закругления пути.

4. Гиря массы 0,2 кг подвешена к концу нити длины 1 м; вследствие толчка гиря получила горизонтальную скорость 5 м/с. Найти натяжение нити непосредственно после толчка.

5. Груз массы 0,102 кг, подвешенный на нити длины 30 см в неподвижной точке, представляет собой конический маятник, причем нить составляет с вертикалью угол 60 0 . Определить скорость груза и натяжение нити.

6. Автомобиль массы 1000 кг движется по выпуклому мосту со скоростью 10 м/с. Радиус кривизны в середине моста 50 м. Определить силу давления автомобиля на мост в момент прохождения через середину моста.

7. Поршень ДВС совершает горизонтальные колебания согласно закону см, где – длина кривошипа, – длина шатуна, – постоянная по величине угловая скорость вала. Определить наибольшее значение силы, действующей на поршень, если масса поршня .

8. Шарик, масса которого равна 100 г, падает под действием силы тяжести и при этом испытывает сопротивление воздуха. Движение шарика выражается уравнением , где – в метрах, – в секундах, ось направлена по вертикали вниз. Определить силу сопротивления воздуха и выразить ее как функцию скорости шарика.

9. Груз массы 1 кг подвешен к тросу длины 2 м и совершает вместе с тросом колебания согласно уравнению , где – угол отклонения троса от вертикали в радианах, – время в секундах. Определить силу натяжения троса в верхнем и нижнем положениях груза.

10. Точка массы движется по эллипсу . Ускорение точки параллельно оси . При координаты точки были , начальная скорость . Определить силу, действующую на движущуюся точку в каждой точке ее траектории.

Тема 6. Определение закона движения по заданным силам (обратная задача динамики).

Вопросы: Основные законы динамики материальной точки (законы Ньютона), понятия силы, массы, инерциальной системы отсчета, принципы независимого действия сил, дальнодействия, причинности, дифференциальное уравнение движения, виды сил в механике.

1. изобразить на рисунке материальную точку в текущем положении и приложенные к ней активные силы;

2. применив закон освобождаемости от связей, изобразить соответствующие реакции связей;

3. выбрать инерциальную систему отсчета, если она не указана в условии задачи;

4. записать систему начальных условий;

5. определить по заданному закону движения ускорение материальной точки и найти его проекции на выбранные оси координат;

6. составить дифференциальные уравнения движения материальной точки;

7. проинтегрировать систему дифференциальных уравнений движения. Использовав систему начальных условий, определить постоянные интегрирования;

8. воспользовавшись найденным законом движения, определить искомые кинематические величины.

ЗАДАЧИ (прямолинейное движение)

1. Найти наибольшую скорость падения шара массы 10 кг и радиуса 8 см, принимая, что сопротивление воздуха равно , где скорость движения, площадь проекции тела на плоскость, перпендикулярную направлению его движения, численный коэффициент, зависящий от формы тела и имеющий для шара значение .

2. Какова должна быть постоянная тяга винта при горизонтальном полете самолета, чтобы, пролетев метров, самолет увеличил свою скорость с м/с до м/с? Тяга винта направлена по скорости полета. Сила лобового сопротивления, направленная в сторону, противоположную скорости, пропорциональна квадрату скорости и равна (Н) при скорости 1 м/с. Масса самолета кг.

3. Определить движение тяжелого шарика вдоль воображаемой прямолинейного канала, проходящего через центр Земли, если принять, что силы притяжения внутри земного шара пропорциональна расстоянию движущейся точки от центра Земли и направлена к этому центру. Шарик опущен в канал с поверхности Земли без начальной скорости. Указать также скорость шарика при прохождении через центр Земли и время движения до этого центра. Радиус Земли равен м, ускорение силы притяжения на поверхности Земли .

4. Точка массы начинает двигаться без начальной скорости из положения прямолинейно (вдоль оси ) под действием силы притяжения к началу координат, изменяющейся по закону . Найти момент времени, когда точка окажется в положении . Определить скорость точки в этом положении.

5. Тело массы 1 кг движется под действием переменной силы Н. Через сколько секунд тело остановится, если начальная скорость тела 20 м/с и сила совпадает по направлению со скоростью тела? Какой путь пройдет тело до остановки?

6. Точка массы начинает двигаться из состояния покоя из положения прямолинейно под действием силы притяжения, пропорциональной расстоянию от начала координат: , и силы отталкивания, пропорциональной кубу расстояния: . При каком соотношении точка достигнет начала координат и остановится?

ЗАДАЧИ (криволинейное движение)

1. Тело веса , брошенное с начальной скоростью под углом к горизонту, движется под влиянием силы тяжести и силы сопротивления воздуха. Определить наибольшую высоту тела над уровнем начального положения, считая сопротивление пропорциональным первой степени скорости: . Найти закон движения точки. На каком расстоянии по горизонтали точка достигнет наивысшего положения.

2. Точка массы движется под действием силы отталкивания от неподвижного центра О , изменяющейся по закону , где радиус-вектор точки.
В начальный момент точка находилась в и имела скорость , направленную параллельно оси . Определить траекторию точки.

3. Точка массы движется под действием силы тяжести по гладкой внутренней поверхности полого цилиндра радиуса . В начальный момент угол , а скорость точки равнялась нулю. Определить скорость точки и реакцию поверхности цилиндра при угле .

Тема 7. Теорема об изменении момента импульса материальной точки.

Вопросы: Понятия центра масс системы материальных точек, момента импульса материальной точки, момента импульса силы, внешние и внутренние силы, замкнутая механическая система, закон сохранения момента импульса системы.

1. изобразить на рисунке систему в текущем положении и приложенные к ней внешние силы;

2. выбрать систему координат (при движении точки по дуге окружности следует одну из осей направить через центр окружности перпендикулярно ее плоскости);

3. вычислить суммы моментов сил, приложенных к материальной точке, относительно осей координат;

4. изобразить вектор импульса точки, записать выражение его моментов относительно неподвижных осей координат и взять от них производные по времени;

5. записать теорему о движении центра масс в проекциях на декартовы оси координат;

6. в зависимости от условия решить прямую или обратную задачу динамики.

1. Два математических маятника, подвешенных на нитях длин и , совершают колебания одинаковой амплитуды. Оба маятника одновременно начали двигаться в одном направлении из своих крайних отклоненных положений. Найти условие, которому должны удовлетворять длины и для того, чтобы маятники по истечении некоторого промежутка времени одновременно вернулись в положение равновесия. Определить наименьший промежуток времени Т.

2. Определить массу М Солнца, имея следующие данные: радиус Земли м, средняя плотность 5,5 т/м 3 , большая полуось земной орбиты а = 1,49 10 11 м, время обращения Земли вокруг Солнца Т = 365,25 сут. Силу всемирного тяготения между двумя массами, равными 1кг, на расстоянии 1м считаем равной Н, где m — масса Земли; из законов Кеплера следует, что сила притяжения Земли Солнцем равна , где г — расстояние Земли от Солнца.

3. Определить движение точки, масса которой 1 кг, под действием центральной силы притяжения, обратно пропорциональной кубу расстояния точки от центра притяжения, при следующих данных: на расстоянии 1 м сила равна 1 Н. В начальный момент расстояние точки от центра притяжения равно 2 м, скорость = 0,5 м/с и составляет угол 45° с направлением прямой, проведенной из центра к точке.

4. Частица М массы 1 кг притягивается
к неподвижному центру О силой, обратно пропорциональной пятой степени расстояния. Эта сила равна 8 Н на расстоянии 1 м. В начальный момент частица находится на расстоянии ОМ₀ = 2м и имеет скорость, перпендикулярную к ОМ₀ и равную 0,5 м/с. Определить траекторию частицы.

Тема 8. Закон сохранения полной механической энергии. Теорема об изменении кинетической энергии системы материальных точек.

Вопросы: Работа силы, кинетическая и потенциальная энергия системы материальных точек, эквипотенциальная поверхность, консервативные и диссипативные силы, закон сохранения механической энергии, теорема об изменении кинетической энергии системы материальных точек.

1. изобразить на рисунке систему в текущем положении и приложенные к ней внешние силы;

2. вычислить сумму работ всех сил, приложенных к материальной точке, на ее перемещении;

3. вычислить кинетическую энергию материальной точки в ее начальном и коечном положениях;

4. применить теорему об изменении кинетической энергии материальной точки и определить искомую величину.

1. Определить наименьшую работу, которую надо затратить для того, чтобы поднять на 5 м тело массы 2 т, двигая его по наклонной плоскости, составляющей с горизонтом угол
в 30 0 . Коэффициент трения 0,5.

2. К концу упругой пружины подвешен груз массы М . Для растяжения пружины на 1 м надо приложить силу в с Н . Составить выражение полной механической энергии груза на пружине. Движение отнести к оси x , проведенной вертикально вниз из положения равновесия груза на пружине.

3. При ходьбе на лыжах на дистанцию в 20 км по горизонтальному пути центр тяжести лыжника совершал гармонические колебания амплитудой 8 см с периодом Т = 4 с , масса лыжника 80 кг , коэффициент трения лыж о снег f = 0,05. Определить работу лыжника на маршруте, если всю дистанцию он прошел за 1 час 30 минут, а также среднюю мощность лыжника. Считать, что работа торможения при опускании центра тяжести лыжника составляет 0,4 работы при подъеме центра тяжести на ту же высоту.

5. Груз массы 1 кг подвешен на нити длины 0,5 м в неподвижной точке О . В начальный момент груз отклонен от вертикали на угол 60 0 , и ему сообщена скорость в вертикальной плоскости по перпендикуляру к нити вниз, равная 2,1 м/с . Определить натяжение нити в нижнем положении и отсчитываемую по вертикали высоту, на которую груз поднимается над этим положением.

6. Путь, по которому движется вагонетка, скатываясь из точки А , образует разомкнутую петлю радиуса r , как показано на рисунке; Ð ВОС = Ð ВО D = α . Найти, с какой высоты h должна скатываться вагонетка без начальной скорости, чтобы она могла пройти всю петлю, а также то значение угла α , при котором эта высота h наименьшая. На участке DC центр тяжести вагонетки совершает параболическое движение.

7. Тяжелая отливка массы т прикреплена к стержню, который может вращаться без трения вокруг неподвижной оси О и отклонен от вертикали на угол φ₀ . Из этого начального положения отливке сообщают начальную скорость .

Определить усилие в стержне как функцию угла отклонения стержня от вертикали, пренебрегая массой стержня. Длина стержня .

8. Груз М веса Р падает без начальной скорости с высоты Н на плиту А , лежащую на спиральной пружине В . От действия упавшего груза М пружина сжимается на величину h . Не учитывая веса плиты А и сопротивлений, вычислить время Т сжатия пружины на величину h и импульс S упругой силы пружины за время Т .

Общие указания к выполнению самостоятельных работ

Все студенты специальности «физика-информатика» выполняют в шестом семестре по три самостоятельные работы, каждая из которых состоит из пяти задач сборника [1]. Номера задач, входящих в самостоятельные работы № 1,2,3 выбираются из приводимых ниже таблиц 1,2,3.

Выбор задач для каждой контрольной работы производится по заданному преподавателем варианту студента. Искомый вариант контрольной работы находится в таблице на пересечении строки, номер которой соответствует числу десятков номера варианта, и столбца с номером, соответствующим числу единиц номера варианта. Так, например, вариант, номер которого 23, содержит в самостоятельной работе 1 задачи 4.27, 2.41, 8.30, 12.8, 12.9 (на пересечении второй строки и третьего столбца таблицы 1).

Следует обратить внимание на то, что задачи сборника
И. В. Мещерского имеют, как правило, два номера: первый является ее порядковым номером в данном издании, а второй (помещенный в скобках) соответствует ее порядковому номеру в предыдущих изданиях. Во всех приводимых далее таблицах порядковые номера задач приводятся по изданиям задачника, вышедшего с 1970 по 1980 гг., в изданиях начиная с 1981 г., номера этих задач заключены в скобки.

Самостоятельные работы выполняется в отдельной тетради, на обложке которой указывается факультет, специальность, фамилия и инициалы студента, а также номер варианта.

При оформлении самостоятельных работ необходимо выполнять следующие правила:

1. в тетради оставляются поля шириной 4-5 см для замечаний преподавателя;

2. текст условия задачи полностью переписывается из задачника;

3. все чертежи выполняются с помощью карандаша, линейки и циркуля; не допускается выполнение чертежей «от руки»;

4. чертежи должны сопровождать решение задачи, даже если они в задачнике не приводятся;

5. на чертежах указываются все необходимые размеры и все векторы, упоминаемые в решении задачи; векторы могут изображаться цветными карандашами;

6. решение задачи аргументируется ссылками на определения, аксиомы или теоремы;

7. решение вначале производится в общем виде, затем в окончательные результаты подставляются числовые значения; следует обратить внимание на четкость изображения всех буквенных символов как на чертежах, так и при вычислениях.

Невыполнение этих правил затрудняет проверку работы и создает трудности при ее защите.

Если после проверки преподавателем какие-либо задачи работы окажутся не зачтенными, то все исправления следует производить в той же тетради на чистых или вклеенных листах, озаглавленных «Работа над ошибками». Каждая самостоятельная работа должна быть защищена студентом очно; в процессе защиты ему предлагаются вопросы, относящиеся к представленному им решению задач; студенту может быть предложено самостоятельно решить фрагмент задачи по одной из тем защищаемой самостоятельной работы.

После защиты всех работ студент допускается к экзамену по курсу.

Указания к выполнению самостоятельной работы 1 (Таблица 1)

Работа содержит три задачи по статике и две по кинематике. Все задачи по статике решаются путем составления уравнений равновесия. При решении задач целесообразна следующая последовательность действий:

1. установить объект равновесия, то есть определить, равновесие какого тела или системы тел исследуется в данной задаче;

2. выявить все связи, изобразить на расчетной схеме их реакции, а также все активные силы;

3. определить, какого рода система сил действует на данный объект равновесия;

4. выбрать оси координат, наиболее удобные для составления уравнений равновесия;

5. составить систему уравнений равновесия для данной системы сил;

6. решить эту систему уравнений относительно неизвестных величин и проанализировать решение.

Приведенную выше последовательность действий необходимо отразить в пояснениях, которые должны сопровождать решение каждой задачи.

Задачи первой строки рассматривают равновесие тел под действием плоской системы сил.

При решении этих задач следует составить и решить три уравнения равновесия плоской системы сил.

Задачи второй строки посвящены равновесию систем тел и решаются методом расчленения. При этом необходимо кроме чертежа из сборника задач изобразить каждый рассматриваемый объект равновесия отдельно и показать все силы, действующие на них.

Задачи третьей строки рассматривают равновесие тел под действи ем пространственной системы сил и решаются путем составления шести уравнений равновесия. При составлении этих уравнений следует иметь в виду, что часть из них может обращаться в тождество. Для облегчения нахождения проекций сил на координатные оси и моментов сил относительно координатных осей полезно изобразить объект равновесия вместе с приложенными к нему силами в трех ортогональных проекциях.

Задачи четвертой и пятой строки относятся к теме «Кинематика точки». В задачах 12.2, 12.5, 12.6, 12.7, 12.13 речь идет о прямолинейном движении точки, а в задачах 12.8, 12.9, 12.12, 12.14, 12.16 — о движении по окружности. Решение задач этих строки необходимо пояснить схемой, изображающей точку в текущем (или заданном) положении, с указанием векторов ее скорости и ускорения (касательного, нормального, полного).

Указания к выполнению самостоятельной работы 2 (Таблица 2)

Задачи первой строки этой контрольной работы относятся к теме «Вращательное движение твердого тела вокруг неподвижной оси и преобразование движений». При этом в задачах 13.5, . 13.17 речь идет о нахождении кинематических характеристик или самого вращающегося тела, или точек, ему принадлежащих. В задачах 13.18, 13.19, 14.2, . 14.12 рассматриваются некоторые простейшие механизмы, для которых необходимо установить соотношения между кинематическими характеристиками движения тел.

Задачи второй и третьей строки решаются при помощи теорем о сложении скоростей и ускорений в сложном движении точки. При решении этих задач необходимо вначале пояснить, что принимается за подвижную систему отсчета каково ее движение и каково движение материальной точки относительно подвижной среды. На схеме необходимо показать положение точки в заданный момент времени или в заданном положении в подвижной системе отсчета. Далее следует указать теорему, используемую при решении задачи. На чертеже изображаются все составляющие абсолютной скорости или абсолютного ускорения точки. Решение рекомендуется выполнять аналитически, проектируя соответствующие векторные равенства на оси выбранной системы координат.

Задачи четвертой строки относятся к теме «Скорости точек плоской фигуры». Решение целесообразно начинать с изображения тела или механизма, о котором идет речь в задаче, в заданном положении. После описания видов движения всех звеньев тела или механизма следует перейти к определению скоростей их узловых точек. При этом можно использовать либо метод полюса, либо теорему о проекциях скоростей двух точек плоской фигуры, либо определять скорости с помощью метода мгновенного центра скоростей.

В задачах пятой строки определяются ускорения точек плоской фигуры. В качестве основного способа решения рекомендуется метод полюса, когда ускорение любой точки плоской фигуры представляется в виде геометрической суммы ускорения полюса, касательного (вращательного) и нормального (центростремительного) ускорений во вращательном движении фигуры вокруг полюса. При этом за полюс выбирается та точка плоской фигуры, ускорение которой либо уже известно, либо может быть легко определено по условию задачи. Решение рекомендуется производить аналитически, проектируя соответствующие векторные равенства на оси выбранной декартовой системы координат.

Указания к выполнению самостоятельной работы 3 (Таблица 3)

Задачи первой и второй строки , относящиеся к теме «Обратная задача дина мики материальной точки «, сводятся к составлению и интегрированию дифференциальных уравнений движения точки при заданных начальных условиях ее движения. При этом рекомендуется соблюдать следующие правила составления уравнений движения:

1. оси инерциальной системы отсчета выбираются так, чтобы в текущем положении координаты точки и проекции ее скорости были положительными;

2. изображаются силы, приложенные к точке;

3. записывается в векторной форме основное уравнение динамики точки;

4. при проектировании этого уравнения на оси координат, получаются дифференциальные уравнения движения точки в выбранной системе отсчета.

В задачах третьей строки рассматривается важный класс динамических задач, посвященных прямолинейному колебательному движению материальной точки. Дифференциальное уравнение движения в этом случае составляется в проекции на ось, совмещаемую с прямолинейной траекторией движения материальной точки. Начало отсчета координат движущейся точки следует совместить с положением ее равновесия. Точка изображается в текущем положении, характеризующимся положительной координатой и положительной скоростью точки. Далее составляется основное уравнение динамики точки в векторной форме, в результате проектирования которого на ось получается дифференциальное уравнение соответствующего колебательного движения точки.

В задачах 32.3. 32.48 рассматривается случай свободных незатухающих (гармонических) колебаний точки. В задачах 32.62. 32.65 рассматриваются свободные затухающие колебания, когда кроме линейной восстанавливающей силы на точку действует еще и сила сопротивления, пропорциональная первой степени скорости. В задачах же 32.78. 32.100 рассматриваются вынужденные колебания точки.

Задачи четвертой строки решаются с помощью двух общих теорем динамики механической системы: теоремы о движении центра масс (35.9, . 35.21) или теоремы об изменении кинетического момента сис темы
(37.4, . 37.53).

Решение этих задач следует начинать с составления расчетных схем, при этом целесообразно придерживаться следующей последовательности действий:

1. выяснить, из каких тел состоит рассматриваемая механическая система;

2. определить вид движения, совершаемого каждым из тел системы;

3. определить, какие внешние силы (активные и реакции связей) приложены к телам системы в ее текущем положении;

4. записать уравнение, выражающее теорему, применяемую для решения задачи, сначала в векторной форме, а затем в виде проекций на оси координат.

При решении задач 35.17, . 35.21 следует доказать, анализируя дифференциальные уравнения движения центра масс системы, постоянство абсциссы центра масс, учитывая начальные условия движения системы. Затем, учитывая это обстоятельство, следует приравнять абсциссы центра масс системы в начальном и конечном положениях. На чертеже при этом рекомендуется изобразить как начальное, так и конечное положения системы.

Задачи 37.4, . 37.27 решаются при помощи дифференциального уравнения вращения твердого тела вокруг неподвижной оси. При этом в задачах 37.15, . 37.27 эти уравнения приводятся к дифференциальным уравнениям свободных крутильных колебаний, интегрирование которых осуществляется точно так же, как и в случае прямолинейных колебаний материальной точки. Задачи 37.42 . 37.57 решаются непосредственно при помощи теоремы об изменении кинетического момента системы. В задачах 37.49 . 37.57 сначала следует доказать, что имеет место случай сохранения кинетического момента относительно данной оси, а затем, используя это обстоятельство, приравнять кинетические моменты системы в начальном и конечном ее положениях.

Задачи пятой строки решаются с помощью теоремы об изменении кинетической энергии системы . Большая часть этих задач решается с помощью этой теоремы в интегральной (конечной) форме, задача же 38.53 решается с использованием дифференциальной формы записи этой теоремы.

В процессе решения этих задач необходимо вычислять кинетическую энергию системы в двух положениях — начальном и конечном; при этом кинетические энергии отдельных тел системы вычисляются по формулам соответствующим движению каждого из этих тел. Работы всех сил, приложенных к телам системы, определяются на перемещениях точек приложения этих сил, соответствующих переходу тел из их начального положения в конечное.

1. Мещерский И.В. Сборник задач по теоретической механике. – М., Наука, 1986.

2. Бать М. И. Теоретическая механика в примерах и задачах / М. И Бать, Г. Ю. Джанелидзе, А. С. Кельзон. – М.: Наука, 1975.

3. Козлова З. П. Теоретическая механика в решениях задач из сборника И .В. Мещерского / З. П Козлова, А. В. Паншина, Г. М. Розенблат. – М.: КомКнига, 2006.

Координатный способ определения движения точки в теоретической механике

Содержание:

Координатный способ определения движения точки:

При координатном способе определения движения точки должны быть даны уравнения движения, т. е. заданы координаты точки как функции времени:

Задание движения точки в прямоугольных координатах

Как известно из курса аналитической геометрии, положение точки M в пространстве может быть определено положением ее проекций P, Q и R на три взаимно перпендикулярные оси (рис. 84), называемые осями координат.

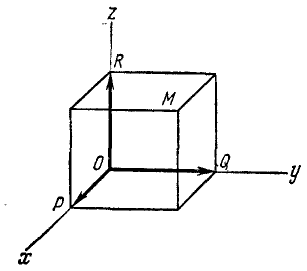
Рис. 84

Положение точки P на оси Ox вполне определяют абсциссой х. Совершенно так же положение точек Q и R определяют ординатой у и аппликатой z.

Если точка M движется относительно осей xOyz, то проекции Р, Q и R перемещаются по осям и координаты точки M изменяются.

Для определения движения точки M нужно знать ее координаты для каждого мгновения, выразить их в функциях времени.

Эти функции непрерывны, так как точка не может из одного положения перейти в другое, минуя промежуточные. Они должны быть однозначны, так как точка занимает в пространстве в каждое мгновение только одно положение.

Соотношения (58) называют кинематическими уравнениями движения точки в прямоугольных координатах, а способ определения движения точки посредством соотношений (58) называют координатным способом определения движения точки. Это название неточно, потому что, кроме прямолинейных прямоугольных координат, существует множество других координатных систем.

Если траектория точки лежит в одной плоскости, то движение точки определяют двумя уравнениями в системе координат xОy: x=x(t), y=y(t).

Следовательно, при координатном способе задания движения точки в пространстве нужно задать ее три координаты, а на плоскости—две координаты как функции времени. Если точка движется прямолинейно, то, приняв прямую, по которой она движется, за ось абсцисс, мы определим движение точки одним уравнением

Если движение точки задано в координатной форме, то для определения ее траектории надо из уравнений движения исключить время

Уравнение траектории

Можно определить траекторию точки, если в уравнениях движения (58) давать аргументу t различные значения и, вычислив соответствующие значения функций, отмечать положения точки по ее координатам. Следовательно. кинематические уравнения движения точки (58) можно
рассматривать как уравнения ее траектории в параметрической форме, а время — как независимый переменный параметр.

Однако более удобно получить уравнение траектории, исключив время из уравнений (58). В самом деле, траекторией называют геометрическое место всех положений движущейся точки, но в геометрии нет понятия времени, а поэтому для получения уравнения траектории нужно из кинематических уравнений движения (58) исключить время t. Если точка движется в плоскости, то, исключив время из уравнений (58′) и (58″), мы получим соотношение, связывающее х и у:

Это уравнение плоской кривой—траектории точки. Если же движение задано тремя уравнениями (58), то, исключив время, получим два уравнения между тремя координатами:
(59 / )

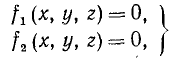
выражающие, как известно из аналитической геометрии, кривую (траекторию) в пространстве. Точнее говоря, уравнения (59) или (59′) выражают кривую, которая полностью или в некоторой своей части является геометрическим местом всех положений движущейся точки.

Иногда бывает нужно выразить в естественной форме движение точки, заданное в прямоугольных координатах уравнениями (58), и, кроме уравнения траектории, дать также уравнение (51) движения точки по траектории. Чтобы его получить, надо продифференцировать уравнения (58) и полученные дифференциалы координат точки подставить в известную из курса высшей математики формулу, выражающую абсолютную величину элемента дуги:

(60)

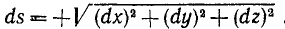
Проинтегрировав (60), мы получим уравнение (51), выражающее длину дуги s как функцию времени, или, что то же, закон движения точки по траектории.

Задача №1

По заданным уравнениям движения точки в координатной форме найти уравнение траектории и уравнение движения по траектории:

1) х = 5 cos 2t, y = 3+5sin 2t;
2) x=21,2 sin 2 t, у = 21,2 cos 2t.

В обоих примерах за единицу длины принят сантиметр, за единицу времени — секунда.

Решение. Чтобы определить уравнение траектории по уравнениям движения, перенесем во втором из заданных уравнений 3 влево, возведем оба уравнения в квадрат и, сложив, получим

Это уравнение окружности с центром в точке: x = 0, y = +3.

Чтобы получить закон движения, продифференцируем заданные уравнения: dx=—10 sin 2t dt, dy = 10 cos 2t dt.

Возводя в квадрат, складывая, извлекая квадратный корень и интегрируя, находим закон движения по траектории:
s=10t + C, где C = s₀.

2) Исключим время из уравнений движения во втором примере:

Это уравнение первого порядка относительно х и у, следовательно, траектория-прямая линия. Прямая отсекает на положительных направлениях осей координат отрезки по 21,2 см. Однако не вся прямая служит траекторией точки: из заданных уравнений видно, что х и у должны быть всегда положительны и не могут быть больше 21,2 см каждый, поэтому траекторией точки является лишь отрезок прямой x+y = 21,2, лежащей в первом квадранте (рис. 85).

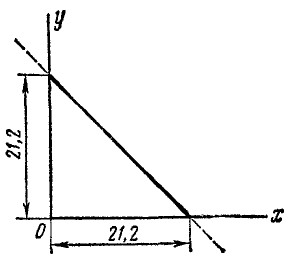
Рис. 85

На этом примере мы видим, что траекторией точки иногда является лишь часть линии, выражаемой уравнением траектории.

Продифференцируем уравнения движения:

dx = 21,2 ∙ 2 sin t cos t dt,
dy = 21,2 ∙ 2 sin t cos t dt.

Теперь no формуле (60) нетрудно найти элемент дуги траектории:

ля получения уравнения (51) движения точки по траектории остается лишь проинтегрировать найденное выражение. Интегрируем и подставляем начальные условия (при t= 0, s₀ = 0):

Ответ. Уравнения траекторий x 2 +(y-3) 2 = 25 и x+y=21,2; уравнения движения по траектории s=10t+s₀ и s = 30 sin 2 t.

Задача №2

Движение точки задано уравнениями:
х = x’ cos φ (t)—y’ sin φ (t),
y = x’ sin φ (t) + y’ cos φ (t),

где х’ и у’ — некоторые постоянные величины, a φ(t)— любая функция времени. Определить траекторию точки.

Решение. Возведем каждое из уравнений в квадрат, а затем сложим их:

x 2 + y 2 = χ ‘2 + y ‘2 .

По условию, х’ и у’ — постоянные. Обозначая сумму их квадратов через r 2 , получим

Ответ. Окружность с центром в начале координат радиуса .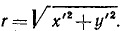

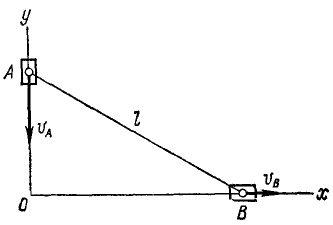
Задача №3

Поезд длиной l м сначала идет по горизонтальному пути (рис. 86, а), а потом поднимается в гору под углом 2α к горизонту. Считая поезд однородной лентой, найти траекторию его центра тяжести.

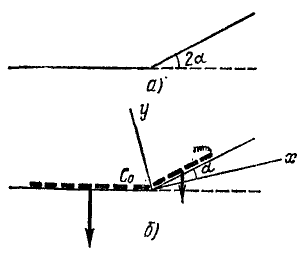
Рис. 86

Решение. Для решения задачи нужно определить координаты центра тяжести поезда, найти уравнения движения центра тяжести и исключить из них время.

Направим оси координат по внутренней и внешней равиоделяшнм угла 2α (рис. 86, б). Траектория центра тяжести поезда не зависит от скорости поезда. Для простоты подсчетов предположим, что он идет равномерно со скоростью υ м/сек и в начальное мгновение t=0 подошел к горе.

Тогда за время t сек на гору поднимется υt м состава поезда и останется на горизонтальном пути l — υt м. Будем считать, что единица длины поезда весит γ.

Применяя формулы (48), найдем координаты центра тяжести поезда:

Координаты центра тяжести представлены здесь как функции времени, следовательно, полученные соотношения являются уравнениями движения центра тяжести поезда. Определяя t (или υt) из первого уравнения и подставляя во второе, найдем уравнение траектории:

Задача №4

Мостовой кран движется вдоль цеха согласно уравнению х = t; по крану катится в поперечном направлении тележка согласно уравнению у = 1,5t (х и у—в м, t — в сек). Цепь укорачивается со скоростью t>=0,5. Определить траекторию центра тяжести груза (в начальном положении центр тяжести груза находился в горизонтальной плоскости хОу, ось Oz направлена вертикально вверх).

Решение. В условии задачи даны лишь два уравнения движения и вертикальная скорость груза:

откуда dz = 0,5dt, и легко получаем третье уравнение:

z = 0,5t

Определив t из первого уравнения, подставим во второе и в третье:

y= 1,5x, z = 0,5x

Координаты груза должны удовлетворять одновременно обоим уравнениям, т. е. траектория лежит одновременно в обеих плоскостях и является линией их пересечения.
Ответ. Прямая.

Алгебраическая величина скорости проекции точки на координатную ось равна первой производной от текущей координаты по времени:

Алгебраическая величина скорости проекции точки на ось

Пусть движение точки M определяется тремя уравнениями:
x =x(t), (58′)
y = y(t), (58″)
z = z(t). (58″‘)

По мере движения точки M в пространстве ее проекции P, Q и R движутся по своим прямолинейным траекториям, т. е. по осям координат, и их движения вполне соответствуют движению точки М.

Так, координата (абсцисса) точки P всегда равна абсциссе точки М, а координаты точек QnR всегда равны ординате и аппликате точки М. Следовательно, при движении точки M в пространстве согласно уравнениям (58) точка P движется по оси Ox согласно уравнению (58′), а точки Q и R— соответственно по осям Oy и Oz согласно уравнениям (58″) и (58″‘).

Таким образом, движение точки M в пространстве можно разложить на три прямолинейных движения ее проекций P, Q и R.

Определим скорость υ_p точки P при движении этой точки по ее прямолинейной траектории Ох, иными словами, определим скорость проекции точки M на ось Ох.

Алгебраическая величина скорости выражается по формуле (53), причем дифференциалом расстояния точки P является дифференциал абсциссы х, а поэтому

(61)

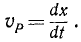
Следовательно, алгебраическая величина скорости проекции P точки M на координатную ось равна первой производной от текущей координаты х по времени t. Она положительна, если точка P движется в положительном направлении оси Ох, и отрицательна, если точка P движется в отрицательном направлении.
Аналогично получаем алгебраические скорости проекций Q и R на ось Oy и на ось Oz:

(61″)

(61″‘)

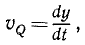
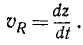
Чтобы получить векторы скоростей проекций, надо умножить величины (61) на единичные векторы:
(61)

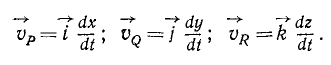
Алгебраическая величина скорости проекции точки на ось равна проекции скорости той же точки на туже ось:

Скорость проекции и проекция скорости

Пусть точка М за бесконечно малый отрезок времени dt передвинулась по своей траектории на элемент дуги ds, абсолютную величину которого выразим формулой (60):

где dx, dy и dz — проекции элемента дуги на оси координат, или, Что то же, элементарные приращения координат точки М.

На рис. 87 эти элементы условно изображены конечными отрезками. Как видно из чертежа, косинусы углов, составляемых элементарным перемещением (а следовательно, и скоростью точки), с осями х, у и z соответственно равны

(62)

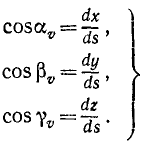
Величина скорости точки M может быть определена по (53):

Чтобы определить проекцию скорости на какую-либо ось, надо умножить абсолютную величину скорости на косинус угла между направлением скорости и направлением этой оси. Таким образом, для проекций скорости точки M на оси координат имеем:

(63′)

(63″)

(63″‘)

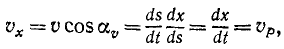
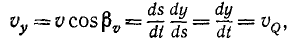
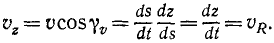
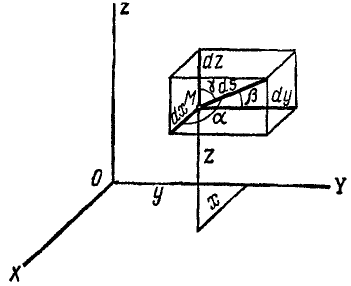
Рис. 87

Равенства (63) словами нужно читать так: проекция скорости точки на ось равна алгебраической скорости проекции точки на ту же ось.

Задача №5

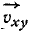
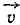
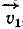
Доказать, что проекция скорости точки M (х, у, z) иа плоскость хОу равняется скорости , с которой движется по плоскости проекция M₁ (х, у, О) точки M на ту же плоскость.

Решение. Скорость 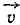точки M составляет с осью Oz угол γ_υ, следовательно, угол, составляемый ею с плоскостью хОу, равен 90° — yυ п косинус этого угла равен sinγ_υ. Поэтому модуль проекции скорости точки M на плоскость хОу

Подводя 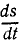под радикал и выражая cosγ_υ, по формуле (62), мы убедимся, что проекция скорости на плоскость равна по величине скорости проекции:

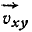
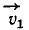
Направления векторов и тоже совпадают, так как направляющие косинусы их одинаковы. Теорема доказана.

Модуль скорости точки равен квадратному корню из суммы квадратов проекций скорости на оси координат:

Модуль скорости. Возведем в квадрат каждое из равенств:
(63)

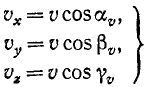
Сумма квадратов направляющих косинусов равна единице и

(64)

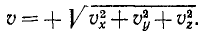
Перед радикалом взят положительный знак, так как величина скорости (ее модуль) всегда положительна. В этом ее существенное отличие от алгебраической величины скорости (53), характеризующей скорость точки при движении по заданной траектории и имеющей знак « + » или «—» в зависимости от направления движения. Величину (64) иногда называют полной скоростью.

Направление скорости можно определить по направляющим косинусам скорости:

Направляющие косинусы скорости

Равенство (64) позволяет определить модуль скорости точки, движение которой задано уравнениями (58). Направление скорости определяется по косинусам углов, составляемых положительными направлениями осей координат с направлением скорости. Значения этих косинусов, называемых направляющими косинусами скорости, мы получим из уравнений (63):

(62′)

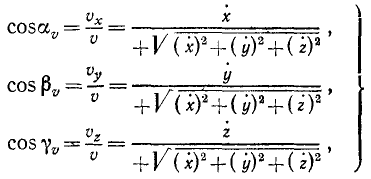
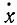
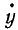
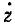
где , и — производные от х, у и z по t.

Если точка движется в плоскости хОу, то γ_υ = 90 o , cosγ_υ = 0 и cos α_υ = sin β_υ.

Задача №6

Уравнения движения суть

Определить траекторию и скорость.

Решение. Из уравнений движения следует, что х и у всегда больше нуля.
Для определения уравнения траектории возведем каждое из уравнений движения в квадрат и составим разность

x 2 — у 2 = a 2

Для определения скорости найдем сначала ее проекции:

а затем уже и полную скорость.

Ответ. Траектория — ветвь гиперболы x 2 — у 2 = a 2 — расположена в области положительных значений х; скорость .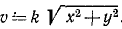

Задача №7

Движение точки задано уравнениями

причем ось Ox горизонтальна, ось Oy направлена по вертикали вверх, υ₀, g и —величины постоянные. Найти траекторию точки, координаты наивысшего ее положения, проекции скорости на координатные оси в тот момент, когда точка находится на оси Ох.

Решение. Уравнения описывают движение тела, брошенного со скоростью υ₀ под углом α₀ к горизонту (к оси Ох).
Чтобы найти уравнение траектории, определим время из первого уравнения и подставим найденное значение во второе; получим

уравнение параболы, проходящей через начало координат (рис. 88).

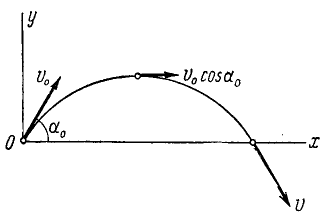
Рис. 88

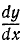
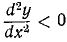
Чтобы определить координаты наивысшего положения, мы можем применить известные из дифференциального исчисления правила нахождения максимума функции, т. е. взять производную , приравняв ее нулю, определить значение х и, подставив его в уравнение траектории, определить соответствующее значение у, убедившись при этом, что вторая производная . Однако мы найдем координаты наивысшего положения точки другим методом, для чего, продифференцировав по времени уравнения движения точки, найдем проекции ее скорости:

Первое из этих уравнений показывает, что проекция скорости на горизонтальную ось постоянна и равна проекции начальной скорости.

Исследование второго уравнения убеждает, что проекция скорости на вертикальную ось в начальное мгновение положительна и равна υ₀ sin α₀; затем, по мере увеличения t, проекция υ_y уменьшается, оставаясь положительной до мгновения 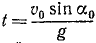, когда υ_y обращается в нуль, после чего υ_y становится отрицательной, возрастая по абсолютной величине с течением времени t.

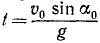
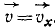
Таким образом, точка движется вправо, сначала поднимаясь, затем опускаясь. Мгновение , при котором точка кончила подниматься, но еще не начала опускаться, соответствует максимальному подъему точки. В это мгновение скорость горизонтальна и . Подставляя найденное значение t в уравнения движения, найдем координаты наивысшей точки траектории:

Определим проекции скорости в мгновение, когда точка находится на оси Ох. В это мгновение ордината точки равна нулю. Приравняем пулю второе из уравнений движения:

Точка находится на оси Ox два раза: при t=0 при

Первое значение t соответствует началу движения, второе —падению точки на ось Ох. Второе значение равно времени всего полета, и оно вдвое больше полученного нами ранее времени наивысшего подъема: время падения равно времени подъема.

Подставляя значение t=0 в уравнения, определяющие проекции скорости, найдем проекции скорости в начальное мгновение:

Подставляя второе из найденных значений t, найдем скорости в момент падения:

Ответ: 1) Парабола

2)

3) υ_x = υ₀ cos α₀, υ_y = 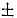υ₀ sin α₀.

причем верхний знак соответствует началу движения, а нижний—концу.

Задача №8

По осям координат (рис. 89) скользят две муфты A и B, соединенные стержнем AB длиной l. Скорость В равна υ_B.

При каком положении муфт скорость муфты А вдвое больше υ_B?

Решение. Координата точки А связана с координатой точки В соотношением

Считая х и у функциями времени и продифференцировав это равенство по времени, найдем зависимость между скоростями обеих точек:

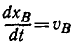
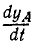
Но и по условию надо, чтобы величина была равна 2υ_B, т. е.

откуда после алгебраических преобразований получаем ответ.

Ответ: 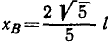(см. задачи № 57 и 89, где даны другие решения).

Проекция ускорения точки на координатную ось равна первой производной по времени от проекции скорости на ту же ось или второй производной от текущей координаты по времени:

Ускорение проекции и проекция ускорения

Ускорение характеризует изменение скорости точки в данное мгновение. Оно выражается пределом отношения изменения вектора скорости к соответствующему промежутку времени при стремлении этого промежутка времени к нулю.

Для того чтобы определить ускорение точки M при ее движении в пространстве, рассмотрим сначала движение по оси Ox точки Р, являющейся проекцией точки M на эту ось.

Пусть в некоторое мгновение t алгебраическая величина скорости точки P была υ_х, а в мгновение t_l = t + Δt стала υ_x+∆υ_x. Тогда ускорение точки P по величине и по знаку выразится пределом

Если знаки υ_x и a_p одинаковы, то движение точки P ускоренное, а если различны, то замедленное.

Аналогично выразятся ускорения проекций Q и R точки M на другие координатные оси:

Проекции υ_x, υ_y и υ_z сами являются производными по времени от координат точки, поэтому ускорения проекций можно выразить вторыми производными по времени от координат точки. Эти равенства характеризуют не только величины, но и знаки ускорений проекций. Иными словами, они выражают изменение алгебраических скоростей проекций P, Q и R в мгновение t.

Только что доказанная теорема о равенстве алгебраической скорости проекции точки на ось и проекции скорости той же точки на ту же ось справедлива для любого момента времени. Следовательно, эта теорема относится не только к скорости, но и к ее изменению в любое мгновение, т. е. к ускорению. Это значит, что написанные выше равенства выражают также проекции a_x, а_у и а_z ускорения а точки M на оси координат O_x, O_y и O_z:

(65)

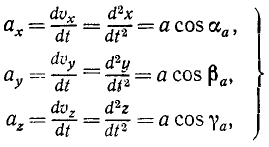
где cosα_a, cosβ_a и cosγ_a—направляющие косинусы ускорения.

Можно рассматривать эти величины (65) как векторы, направленные по осям координат:

(65′)

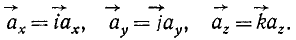
Модуль ускорения точки равен квадратному корню из суммы квадратов проекций ускорения на оси координат:

Величина ускорения при координатном способе задания движения точки

Возведем в квадрат каждое из равенств:

и затем сложим их:

(66)

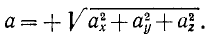
Перед радикалом взят знак плюс, так как модуль вектора—величина положительная. Ускорение точки в отличие от проекций ускорения на оси координат или на другие направления обычно называют полным ускорением. Поэтому равенство (66) можно прочитать так: величина полного ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат.

Направление ускорения можно определить по направляющим косинусам ускорения: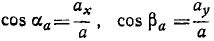
,

Направляющие косинусы ускорения

Направление ускорения определяют по косинусам углов, составляемых положительными направлениями осей координат с вектором ускорения. Формулы направляющих косинусов получаем из уравнений (65):
(67′)

(67»)

(67»’)

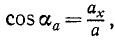
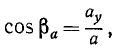
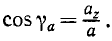
Для определения направления ускорения в каждом конкретном случае надо сначала найти ускорение проекций по (65), для чего необходимо дважды продифференцировать уравнения движения (58), затем найти величину ускорения по (66), а потом определить направляющие косинусы ускорения по (67).

Направление ускорения обычно не совпадает с направлением скорости, и направляющие косинусы (67) ускорения только при прямолинейном ускоренном движении точки постоянно равны направляющим косинусам (62) скорости.

Если точка движется в плоскости хОу, то γ_a = 90 o , cosγ_a = 0, cosα₀ = sin βa.

Задача №9

Точка M движется в системе координат хОу согласно уравнениям х= r cos πt, y=r sinπt, где х и у—в см, a t — в сек. Найти уравнение траектории точки М, ее скорость, направляющие косинусы скорости, ускорение, направляющие косинусы ускорения. Для значений времени t=0; 0,25; 0,5; 0,75, . 2 сек дать чертежи положений точки M, вектора скорости и вектора ускорения.

Решение. Из уравнения движения видно, что координаты точки M являются проекциями на соответствующие оси радиуса-вектора r, составляющего с осью абсцисс угол πt:

Для определения траектории точки исключаем время из уравнений движения. Получаем уравнение окружности

x 2 + y 2 = r 2

Найдем теперь проекции скорости на оси координат, для чего продифференцируем по времени уравнения движения:

откуда по (64) получаем модуль скорости

Величина скорости точки M постоянна.

Направляющие косинусы скорости определим по формуле (62′):

Эти соотношения показывают, что направление скорости непрерывно меняется и что скорость перпендикулярна радиусу-вектору, проведенному из центра О в точку М.

Ускорение точки M найдем по его проекциям, для чего продифференцируем выражения, полученные для проекций скорости:

откуда по (66) получаем величину ускорения

Ускорение характеризует быстроту изменения вектора скорости не только по величине, но и по направлению, поэтому, несмотря на постоянство модуля скорости точки М, ускорение этой точки не равно нулю. Как видно из полученного

Рис. 90

равенства, величина полного ускорения постоянна. Направление ускорения определим по направляющим косинусам согласно (67):

Направление ускорения точки M противоположно направлению радиуса-вектора.
Положения точки M в различные мгновения показаны на рис. 90, а, векторы скорости — на рис. 90,6 и векторы ускорения — на рис. 90, в.

Ответ. Точка M движется по окружности радиуса r против часовой стрелки с постоянной по величине скоростью υ = rπ и с постоянным по величине ускорением a = rπ 2 .

Задача №10

Снаряд выбрасывается из орудия с начальной скоростью υ=1600 м/сек под утлом α₀ = 55 o к горизонту. Определить теоретическую дальность и высоту обстрела, учитывая, что ускорение свободно падающих тел g = 9,81 м/сек 2 .

Решение. Сначала составим уравнения движения снаряда в координатной форме, направив оси, как показано на чертеже (см. рис. 88), для этого определим проекции ускорения:

Разделив переменные, интегрируем:
υ_х= С₁, υ_y = — gt + С2

Подставляя вместо переменных величин их начальные значения, увидим, что C₁ и C₂ равны проекциям начальной скорости:

1600 cos 55 o = C_1, 1600 sin 55 o = — gt + C_2.

Подставим их в уравнения, полученные для проекций скорости:

Разделяя переменные и интегрируя, найдем

При t = 0 координаты снаряда были: х =0, у = 0. Подставляя эти данные, найдем, что C₃ = O и C₄ = O. Значения cos 55° и sin 55° найдем в тригонометрических таблицах. Уравнения движения снаряда примут вид:

Далее поступим, как при решении задачи № 42: приравняв вертикальную скорость нулю, найдем время подъема снаряда (t= 133,7 сек); подставляя это значение t в уравнение движения по оси Оу, найдем теоретическую высоту обстрела (h = 87 636 м); удваивая время /, найдем время полета снаряда (t = 267,4 сек); подставляя это значение- в уравнение движения по оси Ох, найдем теоретическую дальность обстрела (l = 245 393 м).
Ответ. l = 245 км; h = 87,5κм.

• Касательное и нормальное ускорения точки
• Основные законы динамики
• Колебания материальной точки
• Количество движения
• Пара сил в теоретической механике
• Приведение системы сил к данной точке
• Система сил на плоскости
• Естественный и векторный способы определения движения точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.