Виды уравнений и методы их решения
В разработке рассматриваются виды алгебраических уравнений и методы их решения.
Просмотр содержимого документа
«Виды уравнений и методы их решения»
Виды уравнений и методы их решения
Уравнения подразделяются на две большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия, а именно четыре арифметических – сложение, вычитание, умножение и деление, а также возведение в степень и извлечение натурального корня. Трансцендентным называется уравнение, в котором для нахождения корня используются не алгебраические функции: например, тригонометрические, логарифмические и иные.
В курсе математики основной школы рассматриваются только алгебраические уравнения. Рассмотрим более подробно их виды и алгоритм решения.
Группу алгебраических уравнений можно условно разделить на такие виды уравнений как:
целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
иррациональные — алгебраические выражения здесь находятся под знаком корня.
Дробные и иррациональные уравнения можно свести к решению целых уравнений.
Существует также и ещё одна классификация, которая основывается на степени, которая имеется в левой части многочлена. Исходя из этого различают линейные, квадратные и кубические уравнения. Линейные уравнения также могут называться уравнениями первой степени, квадратные — второй, а кубические, соответственно, третьей.
Рассмотрим особенности решения алгебраических уравнений
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Остановимся на основных понятиях.
Тождество — это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв. Для записи тождества наряду со знаком 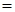
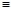
Уравнение — это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:a, b, c. – или теми же буквами, снабженными индексами: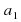
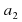
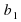
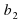
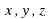
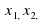
В общем виде уравнение может быть записано так:
F (
В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество (верное равенство), называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения одного уравнения являются решениями другого уравнения, то такие уравнения называют эквивалентными.
Рассмотрим некоторые эквивалентные уравнения:
Уравнение 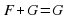
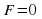
Уравнение 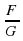
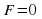
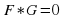
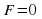
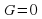
Уравнение 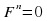
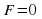
Уравнение 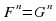
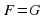
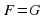
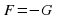
Алгебраическим уравнением называется уравнение вида 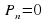
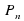
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида:
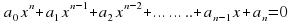
где n – неотрицательное целое число; коэффициенты многочлена называются , ……коэффициентами (или параметрами), называется неизвестным и является искомым. Число n называется степенью уравнения.
Значения неизвестного , обращающие алгебраическое уравнение в тождество, называются корнями (решениями) алгебраического уравнения.
Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейное и квадратное уравнения, а также уравнения вида , где F – одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Так же существуют формулы и для кубического уравнения, но его к простейшим не относят.
Главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка (и) пересечения двух графиков даст решение (я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
Рассмотрим методы решения уравнений.
Линейным уравнением называется уравнение первой степени.
где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень , который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число -b, получаем уравнение
, (2) эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину , получаем корень уравнения (1):
Алгебраическое уравнение второй степени (3),
где a, b, с– некоторые действительные числа, называется квадратным уравнением.
Если , то квадратное уравнение (3) называется приведенным.
Корни квадратного уравнения вычисляются по формуле
Выражение называется дискриминантом квадратного уравнения.
если , то уравнение имеет два различных действительных корня;
если , то уравнение имеет один действительный корень кратности 2;
если , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если ), которое обычно записывается в виде
Корни приведенного квадратного уравнения вычисляются по формуле
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
Корни этого квадратного уравнения удобно вычислять по формуле
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения
связаны с его коэффициентами Формулами Виета
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если , , то оба корня отрицательны;
если , , то оба корня положительны;
если , , то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
если , , уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Перепишем еще раз квадратное уравнение
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
то корни квадратного уравнения вычисляются по формуле
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
Заметим, что , поэтому
но , из формулы (7) поэтому окончательно
Если положить, что + , то
Заметим, что , поэтому
но , поэтому окончательно
Уравнения n-й степени вида
называется двучленным уравнением. При и заменой (2))
где — арифметическое значение корня, уравнение (8) приводится к уравнению
которое и будет далее рассматриваться.
Двучленное уравнение при нечетном n имеет один действительный корень . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и комплексных):
Двучленное уравнение при четном n в множестве действительных чисел имеет два корня , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
Двучленное уравнение при четном n имеет один действительный корней , а в множестве комплексных чисел корней, вычисляемых по формуле
Двучленное уравнение при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
Уравнение имеет два действительных корня .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение имеет два действительных корния и два комплексных корня .
Уравнение действительных корней не имеет. Комплексные корни: .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение действительных корней не имеет. Комплексные корни:
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
оказались «крепким орешком». В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
разделить на , то коэффициент при станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
Чтобы не путаться в коэффициентах, заменим здесь на и перегруппируем слагаемые:
Мы видим, что надлежащим выбором , а именно взяв , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
Если здесь сделать замену , получим кубическое уравнение относительно без члена с :
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу :
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
и взять в качестве сумму и . Заменой , эта система приводится к совсем простому виду:
Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при со знаком минус, а произведение – свободному члену. Отсюда следует, что и — корни уравнения
Выпишем эти корни:
Переменные и равны кубическим корням из и , а искомое решение кубического уравнения (13) – сумма этих корней:
Эта формула известная как формула Кардано.
подстановкой приводится к «неполному» виду
Корни , , «неполного» кубичного уравнения (14) равны
Пусть «неполное» кубичное уравнение (14) действительно.
а) Если («неприводимый» случай), то и
Во всех случаях берется действительное значение кубичного корня.
Алгебраическое уравнение четвертой степени.
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой уравнение сводится к квадратному уравнению с последующим решением двух двучленных уравнений и ( и — корни соответствующего квадратного уравнения).
Если и , то биквадратное уравнение имеет четыре действительных корня:
Если , (3)), то биквадратное уравнение имеет два действительных корня и мнимых сопряженных корня:
Если и , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
можно избавиться от члена подстановкой . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
Идея Феррари состояла в том, чтобы представить уравнение в виде , где левая часть – квадрат выражения , а правая часть – квадрат линейного уравнения от , коэффициенты которого зависят от . После этого останется решить два квадратных уравнения: и . Конечно, такое представление возможно только при специальном выборе параметра . Удобно взять в виде , тогда уравнение перепишется так:
Правая часть этого уравнения – квадратный трехчлен от . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень . При правая часть уравнения (15) принимает вид
а само уравнение сводится к двум квадратным:
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
и добавим к обеим частям выражение , чтобы в левой части образовался полный квадрат:
Теперь приравняем к нулю дискриминант правой части уравнения:
или, после упрощения,
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: . После подстановки этого значения получим уравнение
откуда . Корни образовавшихся квадратных уравнений — и . Разумеется, в общем случае могут получиться и комплексные корни.
подстановкой приводится к «неполному» виду
Корни , , , «неполного» уравнения четвертой степени (16) равны одному из выражений
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие
причем , и — корни кубичного уравнения
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени ( ) можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени при неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его «Мемуаре об условиях разрешимости уравнений в радикалах» (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
Если несократимая дробь является корнем многочлена с целыми коэффициентами, то ее числитель является делителем свободного члена , а знаменатель — делителем старшего коэффициента .
Для доказательства достаточно подставить в уравнение и умножить уравнение на . Получим
Все слагаемые в левой части, кроме последнего, делятся на , поэтому и делится на , а поскольку и — взаимно простые числа, является делителем . Доказательство для аналогично.
С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа «кандидатов». Например, для уравнения
старший коэффициент которого равен 1, «кандидатами» будут делители числа –2. Их всего четыре: 1, -1, 2 и –2. Проверка показывает, что корнем является только одно из этих чисел: .
Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,
остаток от деления многочлена на двучлен равен , т. е. .
Из теоремы непосредственно следует, что
Если — корень многочлена , то многочлен делится на , т. е. , где — многочлен степени, на 1 меньшей, чем .
Продолжая наш пример, вынесем из многочлена
множитель . Чтобы найти частное , можно выполнить деление «уголком»:
Способы решения квадратных уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Тема урока «Способы решений квадратных уравнений»
Дата проведения 26.01.2022г.
Тип урока: закрепление и расширение ранее полученных знаний
Предметные: знать понятия: «квадратное уравнение», «квадратный трехчлен», название его коэффициентов, виды приведенного, полного и неполного квадратных уравнений; уметь преобразовывать квадратное уравнение к стандартному виду, определять приведенные и неполные квадратные уравнения, решать неполные квадратные уравнения и полные, определять по дискриминанту число корней полного квадратного уравнения и определять эти корни по формулам.
Личностные: формирование ответственного отношения к успешной учебной деятельности, воспитание трудолюбия, взаимопомощи, математической культуры.
регулятивные – уметь сравнивать, сопоставлять, анализировать, делать выводы, выполнять самоконтроль, взаимопроверку и самопроверку;
коммуникативные – уметь вести диалог, слушать, аргументировано высказывать свои суждения, быстро включаться в деятельность на уроке, взаимодействовать с одноклассниками;
познавательные – уметь читать математический текст и находить информацию в учебнике по заданной теме, работать по правилу, алгоритму, образцу, логически мыслить, рассуждать, доказывать утверждения
Цель урока: Обобщение темы: «Квадратное уравнение»; создание условий для осознанного и уверенного владения навыком решения квадратных уравнений, рассмотрение различных способов решения квадратных уравнений
Образовательные задачи урока: систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений, расширить и углубить представления учащихся о решении уравнений, организовать поисковую деятельность учащихся при решении квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
Развивающие задачи урока:
· развивать математическое мышление, память, внимание;
· развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
· развивать коммуникативные навыки; навыки самостоятельной работы;
· привить любовь к предмету, желание познать новое.
Воспитательные задачи урока:
· воспитывать культуру умственного труда;
· воспитывать культуру коллективной работы;
· воспитывать информационную культуру;
· воспитывать потребность добиваться успехов в приобретении знаний; воспитание навыков самоконтроля и взаимоконтроля, развитие самостоятельности и творчества.
Планируемые результаты: результатом деятельности учащихся на уроке является понимание сути различных способов решения квадратных уравнений, осознанный и вдумчивый подход к анализу, поиску новых способов. Открытия для себя нового, осознание чувства сопричастности к общему успеху.
Основные термины, понятия: квадратное уравнение, коэффициенты квадратного уравнения, приведённое – не приведённое квадратное уравнение, полное – неполное квадратное уравнение
Оборудование: компьютер, проектор с интерактивной доской, презентация, листы учета знаний, карточки с заданиями.
1. Организационно-мотивационный момент (1-2 мин)
2. Целеполагание (4-5 мин)
3. Актуализация знаний по теме «Способы решений квадратных уравнений» (5-6 мин)
4. Подготовка учащихся к работе на основном этапе (5-6 мин)
5. Этап психологической разгрузки (1-2 мин)
6. Закрепление умений и навыков по изучаемой теме (9 мин)
7. Саморазвитие и конструирование полученных знаний по теме (8 мин)
8. Подведение итогов урока и задание на дом (4-5 мин)
9. Рефлексия (3-4 мин)
I. Организационно — мотивационный момент
Учеба – это книга, которую можно с интересом читать, перелистывая страницу за страницей, обогащаясь знаниями, «расти» умом. Сегодня мы с вами продолжим читать главу «Квадратные уравнения» − очень важную для изучения курса математики средней школы. Покажем не только знания, но и свои умения и навыки по этой теме.
Рассмотрите уравнения, на слайде, и выберете те уравнения, которые нужно исключить из данной группы и объясните почему. (слайд №2)
А, как вы думаете, какая тема сегодняшнего урока?
(Тема: Квадратные уравнения и способы их решений» Что будет сегодня на уроке в роли «главного героя»?
(«Способы решения квадратных уравнений»)
Кто может сформулировать цель нашего урока?
( Цель урока: Сегодня мы повторим способы решения квадратных уравнений) (слайд №3)
Работают со слайдом презентации
Делают определенные умозаключения
III. Актуализация знаний по теме
1.А что же такое квадратное уравнение? Дайте определение квадратного уравнения.
(Квадратным уравнением называют уравнение вида ax 2 + bx + c =0, где коэффициенты a , b , c – любые действительные числа, причем a 
А сейчас я предлагаю вам следующее задание.
2. Составьте квадратное уравнение с заданными коэффициентами a , b и c в тетрадях и по желанию выходите и записывайте уравнения в таблицу.(слайд №5)
(Учащиеся выходят к доске и записывают полученные уравнения)
3.На какие группы можно разбить полученные уравнения? (Полные – 3,4 и неполные уравнения – 1,2,5).
4.Какие уравнения называются полными? Неполными?
(Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого b и c отличны от нуля. (слайд№6)
Неполное квадратное уравнение – это уравнение, у которого присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b или c равен нулю) .(слайд №7)
5.На какие еще группы можно разбить данные уравнения? (Приведенные – 4,5 и неприведённые – 1,2,3)
6.Какие уравнения называются приведёнными? Неприведёнными? (Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; квадратное уравнение называют неприведенным, если его старший коэффициент отличен от 1).(слайд №8)
Выполняют задания педагога в тетрадях, отвечают на вопросы, ведут совместное обсуждение вопросов, вступают в беседу при ответах
IV. Подготовка учащихся к работе на основном этапе
Ребята, сейчас вы поработаете в парах. На листочках у вас написан способ, которым вы должны решить квадратное уравнение и затем защитить своё решение. Решать мы будем одно квадратное уравнение
3х 2 +2х-1=0 и постараемся вспомнить все способы, которые мы уже знаем. (слайд №9)
1 способ: «По общей формуле, через дискриминант»
2 способ: «Разложение левой части уравнения на множители способом группировки»
3 способ: «По сумме коэффициентов квадратного уравнения»
Работают в парах, решают уравнение в тетради, определенным способом, аргументируют способ решения.
От каждого способа по одному представителю, решение уравнения у доски с аргументацией.
Остальные учащиеся соглашаются или нет, доказывая свое мнение
V. Этап психологической разгрузки (физминутка)
На уроке мы сидим
И во все глаза глядим,
А глаза нам говорят,
Что они уже болят.
Мы закроем наши глазки
И расскажем без подсказки.
Три способа прошли
Зажмурьтесь дружно от души.
Каким вам легче способом решать
На пальцах нужно показать.
Открываем мы глаза
Дальше нам решать пора.
Продолжаем мы урок
Всем пошел наш отдых впрок.
Расслабляются и выполняют упражнения
VI. Закрепление умений и навыков по изучаемой теме
Составьте квадратное уравнение, используя следующие данные и вы сможете найти ответ задачи. (задачи на раздаточных листах)
А) Многие, уходя из кабинета, не выключают свет. Да и дома порой зажигают все лапы, когда в этом нет необходимости. Кто-то может сказать: мелочь! Между тем сосчитайте, сколько за 10 часов расходует одна лампочка в 100 Вт. Ответ переведите в кВт. Полученное число будет первым коэффициентом квадратного уравнения. Ответ: 
Б) А что такое капля воды из неплотно закрытого крана? За час теряется 0,6л, а за сутки – .. ? (14,4л воды). В данном числе сложите цифры. Полученное число будет вторым коэффициентом. Ответ: 14.4л, 1+4+4 = 9, в=9.
В) К обеду школа получает 35 кг хлеба, в бачках для отходов остаётся 


Г) Все коэффициенты положительные числа. Составьте квадратное уравнение, решите его. Ответ: у 2 +9у+14=0; у1 = -7,у2 = -2.
Решают предложенные задачи в парах (каждый ребенок на своем уровне, кто сколько успеет)
VII. Саморазвитие и конструирование полученных знаний по теме
Ещё одна страница главы «Квадратные уравнения» нашей книги перевернута. Но процесс познаний бесконечен, как бесконечны открытия, совершаемые человечеством. Итак, открытия продолжаются.
Сегодня на уроке мы познакомимся с новым способом решения квадратных уравнений, который не изучается в школе. Но он очень интересный и вовсе не сложный.
Сейчас я вам его попробую продемонстрировать. Если будут возникать вопросы сразу же их задавайте.
Решите квадратные уравнения, заполните таблицу, занося в таблицу коэффициенты и корни квадратного уравнения, найдите закономерность в нахождении корней квадратного уравнения:
Используя эти свойства, решите данные уравнения (слайд 10)
Вывод: (слайд 11) (чтобы решать квадратные уравнения, нужно знать формулы – это обязательно. Но, чтобы быстро и устно решать некоторые уравнения, нужно умение анализировать. Если хорошо потренироваться, то решение любого уравнения не вызывает затруднений.)
Познают через демонстрацию новый способ решения квадратных уравнений.
Самостоятельно решают в тетради квадратные уравнения, применяя новый способ
VIII. Подведение итогов урока и задание на дом
Выбрать из учебника несколько уравнений, которые можно решить, используя формулы, полученные на уроке и решить их.
Решить уравнение 3х 2 — 2х – 1 = 0 разными способами.
Давайте оценим нашу деятельность на уроке:
поднимите руку, у кого все получилось и кто сможет помочь своему товарищу
поднимите руку, у кого еще остались вопросы
(учащиеся, работающие у доски и активно работающие на уроке получают положительные оценки, все остальные получают оценки, после проверки письменных работ)
Обсуждают домашнее задание
Наш урок подходит к концу, подумайте о том с какой пользой для вас прошёл этот урок, в этом я вам помогу, начните свой ответ с любого из предложений: (слайд 11)
· Я хорошо знаю, что .
· Я должен знать, что ..
· Сегодня я понял, что…
· Урок дал мне для жизни…
Проводят рефлексию своей деятельности на уроке
1 способ: «По общей формуле, через дискриминант»
2 способ: «Разложение левой части уравнения на множители способом группировки»
3 способ: «По сумме коэффициентов квадратного уравнения»
А) Многие, уходя из кабинета, не выключают свет. Да и дома порой зажигают все лапы, когда в этом нет необходимости. Кто-то может сказать: мелочь! Между тем сосчитайте, сколько за 10 часов расходует одна лампочка в 100 Вт. Ответ переведите в кВт. Полученное число будет первым коэффициентом квадратного уравнения.
Б) А что такое капля воды из неплотно закрытого крана? За час теряется 0,6л, а за сутки – .. ? (14,4л воды). В данном числе сложите цифры. Полученное число будет вторым коэффициентом.
В) К обеду школа получает 35 кг хлеба, в бачках для отходов остаётся часть этого хлеба. Труд скольких людей пропадает зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число. Полученное число будет третьим коэффициентом.
Г) Все коэффициенты положительные числа. Составьте квадратное уравнение, решите его.
Список использованной литературы:
1. Алгебра. Учебник для 8 класса общеобразовательных учреждений под редакцией С. А.Мордковича. – М.: Просвещение, 2018.
2. В.И. Жохов, Ю. Н. Макарычев, Н.Г. Миндюк. Дидактические материалы по алгебре для 8 класса. – М.: Просвещение, 2018.
3. Ковалева Г. И. Уроки математики в 8 классе. Поурочные планы. Часть 2.- Волгоград: Гринина Е. С.,2015.-64с.
4. Н.Л.Барсукова Открытые уроки алгебры. 7-8 классы; Москва; ВАКО; 2016г.
Самоанализ урока алгебры 8 класса на тему «Способы решений квадратных уравнений»
1. Внешние связи урока.
Урок в 8 классе по теме «Способы решений квадратных уравнений» мною был проведен согласно календарно-тематическому планированию. Это урок закрепления и расширения ранее полученных знаний по данной теме. В теме «Квадратные уравнения» это 15 урок по счёту. Всего в теме 23 урока. Ранее проведенные уроки были посвящены первичным понятиям квадратных уравнений и отработке навыков их решения:
· коэффициенты квадратного уравнения,
· стандартный вид квадратного уравнения,
· приведённое – не приведённое квадратное уравнение,
· полное – неполное квадратное уравнение,
· способы решений неполных квадратных уравнений.
На последующих уроках планируется рассмотреть другие способы решений квадратных уравнений, их применение на практике при построении моделей реальных ситуаций на расчёт геометрических задач, движения, работы, сплавов, процентного содержания веществ и т.д., а также для решения рациональных уравнений. В дальнейшем при изучении данной темы в 8 классе, а также сдачи ОГЭ в 9 классе пригодятся знания, полученные на этом уроке. Пригодятся они и на уроках химии при расчётах сложных составов сплавов и смесей, физики — при изучении оптики, равноускоренного движения, при работе с векторами.
2. Характеристика триединой цели урока с опорой на характеристику класса.
Перед уроком была поставлена триединая дидактическая цель урока, которая реализовывалась через следующие аспекты согласно требованиям ФГОС ОО 2013 года:
Предметные: знать понятия: «квадратное уравнение», «квадратный трехчлен», название его коэффициентов, виды приведенного, полного и неполного квадратных уравнений; уметь преобразовывать квадратное уравнение к стандартному виду, определять приведенные и неполные квадратные уравнения, решать неполные квадратные уравнения и полные, определять по дискриминанту число корней полного квадратного уравнения и определять эти корни по формулам.
Личностные: формирование ответственного отношения к успешной учебной деятельности, воспитание трудолюбия, взаимопомощи, математической культуры.
регулятивные – уметь сравнивать, сопоставлять, анализировать, делать выводы, выполнять самоконтроль, взаимопроверку и самопроверку;
коммуникативные – уметь вести диалог, слушать, аргументировано высказывать свои суждения, быстро включаться в деятельность на уроке, взаимодействовать с одноклассниками;
познавательные – уметь читать математический текст и находить информацию в учебнике по заданной теме, работать по правилу, алгоритму, образцу, логически мыслить, рассуждать, доказывать утверждения.
Поставленные цели урока вытекают из наблюдений за классом, его актуальным развитием. По своей алгебраической компетенции класс очень разнообразен, есть дети с высоким уровнем развития, а есть дети слабые. Поставлены реальные цели образовательного, развивающего и воспитательного аспектов. Цели данного урока соответствуют стандартным требованиям программы и связаны с предыдущими учебными занятиями.
По структуре я выбрала комбинированный урок, поскольку он сочетает различные виды деятельности.
3. Характеристика замысла урока. Характеристика этапов урока.
I. Общая организация урока
1. Последовательность и распределение этапов урока по времени.
Все этапы урока были направлены на реализацию поставленных целей с учетом особенностей класса.
Оргмомент , включал в себя предварительную организацию класса, мобилизующее начало урока, мотивацию деятельности учащихся, создание психологической комфортности и подготовку учащихся к активному и сознательному усвоению нового материала. Подготовка класса и каждого ученика была проверена мною визуально.
Подготовке учащихся к активному и сознательному усвоению нового материала способствовало целеполагание, т.о. моя деятельность и деятельность учащихся были объединены одной целью.
Следующий этап – мотивационно — ориентировочный. Дидактической задачей этого момента урока являлось возбуждение интереса к материалу, пробуждение творческой мысли, осознанное принятие учащимися цели познавательной деятельности. Создание мотивации при актуализации знаний нацелило учащихся на активную работу в изучении темы, на осознание главных аспектов изучаемого материала его систематизацию и отбор.
Рефлексивно – оценочный. Его дидактическая задача – воспроизведение опорных знаний предыдущего урока, установление осознанности их понимания, полноты и правильности их применения. На этом этапе мне удалось вовлечь учащихся в процесс активного взаимодействия по реконструкции ранее изученного материала.
Следующий этап — применение способов действий, входящих в данное знание. В ходе выполнения самостоятельной работы ребята получили достоверную информацию о достижении собственных планируемых результатов. На этом этапе удалось определить уровень усвоения материала и приступила к устранении типичных ошибок у ребят и доведению знаний учащихся до обязательного уровня. Были созданы условия, обеспечивающие процесс самостоятельного применения знаний и способов действий. Они состоят из индивидуальной самостоятельной работы, контроля, взаимоконтроля, самооценки, практики под руководством учителя, коррекции. Мною были созданы условия, требующие от учащихся пробы своих возможностей самоопределения, самоутверждения, самооценки (развитие рефлексивных качеств).
Учащиеся на этом этапе работали практически самостоятельно. Моя роль на данном этапе заключалась в координации и консультации (индивидуальной). Я занимала позицию: «Я рядом. Я с вами». По окончанию самостоятельной работы, с помощью решений на доске, представителями способов решения, учащиеся осуществили взаимопроверку. Результаты обсуждались коллективно в уважительном тоне с акцентом на значимость умений и навыков.
Рассмотрение нового способа решения. Этот этап урока начался с предоставления готового решения, а именно формулы в буквенно-знаковой форме. Это позволило учащимся несколько расслабиться, отдохнуть, но в то же время и не потерять нить урока его значимость. После рассмотрения нового материала учащиеся приступили к самостоятельной работе. На данном этапе я оказывала помощь учащимся, которые просили ее.
Следующий этап – закрепление основных понятий. Дидактическая цель – анализ, самоанализ и оценка успешности достижения планируемых результатов. Эти цели я достигла с помощью решения упражнений из задачника, создала мотивацию через анализ достигнутого, сравнение прошлого и настоящего. Со стороны учащихся я почувствовала проявление заинтересованности в работе, стимулирование к личным достижениям. Этот этап послужил адекватности самооценки учащихся оценке учителя, получение ими информации о реальных результатах своей деятельности.
Очередной этап – задание на дом. На ряду с теоретическим материалом и упражнениями на отыскание корней уравнений по формулам, я включила задания, которые учащиеся могут подготовить учитывая свой уровень обученности по данной теме.
Завершающий этап – рефлексия. На данном этапе каждый ребенок может для себя определить уровень знания и незнания по данной теме.
2. Организация познавательной деятельности на уроке (сочетание фронтальной, групповой, индивидуальной работы).
В ходе урока четко прослеживались этапы урока, соответствующие технологии развития критического мышления: вызов, стадия осмысления, понимание, рефлексия.
На стадии изучения материала организовывалась совместная работа педагога с учащимися по ходу изучения материала, при самостоятельном выполнении заданий. Это позволило осмыслить прочитанное, установить причинно-следственные связи и, при необходимости, можно было оказать индивидуальную помощь учащимся. В ходе проведения урока использовалась одна из эффективных форм коллективной познавательной деятельности парная работа, при которой были созданы условия для проявления и развития каждого ребенка.
По составу обучающихся были сформирована гетерогенные пары, то есть, объединяя детей разного уровня обученности и подготовленности. Обучение осуществляется путем общения, когда каждый учит каждого (взаимное обучение). Таким образом, урок построен на самостоятельной работе обучающихся и консультативной помощи учителя.
Дифференцированный подход осуществлялся при работе в парах, при выполнении самостоятельной работы, в домашнем задании. Основные формы контроля – индивидуальная и фронтальная. Вид контроля – тематический.
3. Соблюдение охранительного режима.
Охранительный режим работы заключался в смене видов деятельности, психологическая разгрузка. Презентация, разработанная к уроку, соответствует нормам зрительного восприятия и цвета и формы.
4. Подведение итога урока. На завершающем этапе урока был подведён итог, проведена рефлексия, в ходе которой дети оценили свою работу. Домашнее задание соответствует нормативным требованиям, задано с комментарием с целью правильного и успешного его выполнения. Оценки выставлены.
1. Научная, воспитательная и развивающая направленность урока.
При подготовке к уроку мною были поставлены следующие цели:
Предметные: знать понятия: «квадратное уравнение», «квадратный трехчлен», название его коэффициентов, виды приведенного, полного и неполного квадратных уравнений; уметь преобразовывать квадратное уравнение к стандартному виду, определять приведенные и неполные квадратные уравнения, решать неполные квадратные уравнения и полные, определять по дискриминанту число корней полного квадратного уравнения и определять эти корни по формулам.
Личностные: формирование ответственного отношения к успешной учебной деятельности, воспитание трудолюбия, взаимопомощи, математической культуры.
регулятивные – уметь сравнивать, сопоставлять, анализировать, делать выводы, выполнять самоконтроль, взаимопроверку и самопроверку;
коммуникативные – уметь вести диалог, слушать, аргументировано высказывать свои суждения, быстро включаться в деятельность на уроке, взаимодействовать с одноклассниками;
познавательные – уметь читать математический текст и находить информацию в учебнике по заданной теме, работать по правилу, алгоритму, образцу, логически мыслить, рассуждать, доказывать утверждения.
Поставленные в начале урока цели были тесно связаны на уроке и полностью реализовались при проведении. Весь излагаемый на уроке материал полностью соответствовал теме урока, был необходим ученикам для выполнения практической части и основывался на материале учебника. Реализация воспитательного потенциала урока достигается при условии решения воспитательных задач в ходе урока в единстве с задачами обучения и развития личности школьника; целенаправленного отбора содержания учебного материала, использования современных образовательных технологий; организации творческой исследовательской деятельности учащихся на уроке и при выполнении домашних заданий. Технологии, применяемые на уроке, предполагали активную деятельность учащихся на разных уровнях познавательной самостоятельности. Именно в этом заключалось важнейшее условие реализации воспитательного потенциала данного урока. Я пыталась воспитывать у учащихся логическую культуру мышления, строгость и стройность в умозаключениях; расширять кругозор учащихся, поднимать их общий культурный уровень через общение и решение математических задач.
На уроке требую каждый шаг своего решения аргументировать и доказывать свое мнение. Кроме того, благодаря точному ответу в математических заданиях, каждый ученик может после выполнения задания достаточно точно и объективно оценить свои знания и меру усилий, вложенных в работу, то есть дать себе самооценку, столь важную для формирования личности. Призываю своих учеников при самооценке быть предельно честным и объективным, терпимым в преодолении сложностей при решении заданий. Воспитываю в учениках трудолюбие, настойчивость, упорство, умение соглашаться с мнением других, доводить дело до конца, ответственность.
2. Правильность подбора учебного материала на уроке.
Содержание учебного материала на уроке осуществляло взаимосвязь всех его компонентов. Отбор его был обусловлен его целями. Основное содержание учебного материала определено программой и отвечает требованиям государственных стандартов, а так же ориентировано на личностное развитие и саморазвитие ученика.
Примеры для самостоятельного решения и проверки знаний были тщательно отобраны. Для этого были использованы самые разные источники информации. Прежде всего, это учебник и прилагаемый к нему учебно-методический комплекс, затем дополнительная и справочная литература, интернет ресурсы. Были использованы материалы, которые не обсуждаются в учебнике.
Содержание учебного материала было тщательно отобрано, научно обосновано, логически выстроено, доступно и экономно по времени. Выделять главное — довольно непростая проблема, суть которой в рациональном расположении главного в системе связей учебника; выделении его из общего текста всевозможными средствами. Учить этому искусству следует и учеников. На материале темы показано, что в содержании данной темы нужно запомнить надолго, что передать своими словами, а что только бегло просмотреть. На учебном материале я учила учеников выделять главное, что способствовало достижению запланированных целей урока.
3. Связь теории с практикой.
Бернард Шоу утверждал: «Единственный путь, ведущий к знанию, — это деятельность. Чтобы знание становилось инструментом, а не залежами ненужного старья, ученик должен с ним работать. » Привлекая детей к поиску новых знаний, я всегда стремлюсь объяснить и вместе обсудить для чего необходимо то или иное знание, как оно пригодится в жизни. Поэтому и на этом уроке пытаюсь им объяснить значимость умения решать квадратные уравнения, приводя соответствующие примеры.
4. Организация повторения на уроке и его содержание. Связь повторенного с новым материалом.
Изучение нового материала не возможно без применения ранее изученных знаний, поэтому были актуализированы знания, необходимые для работы над новым материалом, при изучении нового способа решения квадратных уравнений. Одновременно шла эффективная работа над развитием речи, мыслительных операций, о чем свидетельствовала деятельность учащихся. При выполнении заданий, самопроверке и взаимопроверке, предыдущие знания были актуализированы и активно использовались при дальнейшем изучении темы.
5. Уровень знаний, умений, навыков учащихся.
Активная деятельность ребят, их ответы и быстродействие при решении заданий показали высокий уровень усвоения темы. Из 25 человек присутствующих на уроке дети получили 15 — «5» и 10 — «4». Все оценки были аргументированы и обоснованы. Решение тренировочных упражнений позволило закрепить новые знания и оценить степень усвоения материала. Деятельность учащихся была построена так, что каждый ребенок смог себя проверить, осознать: все ли он понял, запомнил ли запись, решение. Считаю, что на данном этапе каждый ученик смог пережить ситуацию успеха, убедиться, что тема урока ими освоена, о чем свидетельствовали результаты их самооценки и рефлексии.
III. Методическая сторона урока и его оборудование
1. Качество методов и приемов обучения, их адекватность задачам урока и уровню развития познавательных возможностей детей.
По структуре я выбрала комбинированный урок, поскольку он сочетает различные виды деятельности.
Формы организации деятельности учащихся: фронтальная, индивидуальная, работа в парах.
Оборудование: компьютер, мультимедийный проектор.
Структура урока соответствует типу урока и его дидактическим задачам. На уроке были использованы следующие методы обучения:
— словесные (беседа с учащимися);
— наглядные (демонстрация презентации);
На уроке использовались информационно-компьютерные средства для активизации познавательной активности, повышения качества образования учащихся. Были использованы следующие формы познавательной деятельности: фронтальная, индивидуальная, которые в ходе урока сменяли друг друга.
Время, отведенное на все этапы урока, было рационально распределено. Поддерживался высокий темп работы учащихся. Выбранные мною формы и методы обучения способствовали созданию на уроке положительной психологической атмосферы. Общение учащихся и учителя доброжелательное, доверительное. По моему мнению, урок прошел успешно, реализованы все поставленные дидактические цели и задачи урока
2. Функциональный анализ урока. При повторении теоретического материала учащиеся работали по заранее составленным для них вопросам. Ответы были положительные. Урок был построен оптимально, он соответствовал уровню учебной подготовки и развития учащихся. Структура урока выбрана рационально, время, отведённое на этапы урока, было достаточным.
Взаимосвязь между этапами урока была плавной, логичной. Помощь учителя была минимальной, направляющей работу класса и каждого в отдельности. Акцент делался на умение решать квадратные уравнения. Опора на знания — это залог успеха урока.
3. Оценка конечного результата урока. По моему мнению, урок прошел успешно, реализованы все поставленные дидактические цели и задачи урока. Урок прошел на высоком эмоциональном уровне: и учащиеся, и я получили огромное удовольствие от общения. Особенным вниманием у учащихся пользовался момент защиты способа решения уравнения. Ребята участвовали в подведении итогов урока. Отметки за урок выставлены и прокомментированы.
Работа по данной теме будет продолжена, т.к решение квадратных уравнений – база знаний для учащихся.
Теоретические основы формирования понятия уравнения в начальной школе; методика введения понятия уравнение на примере разных УМК
статья по математике (2 класс)
В настоящее время сложно представить школьный курс математики без понятия уравнение. Большинство задач сводятся к решению и применению различных видов уравнений. При этом уравнения, являются одним из средств моделирования явлений из окружающего нас мира и знакомство с ними, а также они являются существенной частью математического образования.
Понятие уравнение относится к важнейшим общематематическим понятиям. Именно поэтому затруднительно предложить его определение, одновременно и строгое, и доступное для учащихся, приступающих к овладению школьным курсом математики.
В словаре по педагогике под редакцией В.А. Мижерикова, дается следующее определение понятию уравнения – это два выражения, которые соединены знаком равенства и в них входят одна или несколько переменных, называемых неизвестными.
Е.А. Крапивина, говорит о том, что уравнение, представляет собой равенство, содержащее в себе неизвестное число, значение которого нужно найти.
И.А. Моргунова, указывает на то, что понятие уравнение, является равенством, которое выполняется только при некоторых значениях входящих в него букв. Буквы, которые входят в состав уравнения, могут быть неравноправными: одни могут принимать все свои допустимые значения, а другие, значения которых требуется отыскать, называют неизвестными данного уравнения (как правило, их обозначают последними буквами латинского алфавита x, y, z, u, v, w).
Рассмотрев множество определений понятия уравнение можно сделать вывод, что уравнение – это вид равенства с неизвестной величиной, которая чаще всего обозначается латинской буквой. При этом числовое значение данной буквы, позволяющее получить верное равенство, называется корнем уравнения.
В школьном курсе математики термин «уравнение» называют «выражение» или «предложение с переменной».
Можно выделить основные признаки понятия уравнение:
— содержит букву, значение которой неизвестно и его надо найти
Понятие «решить уравнение», является центральным.
Решение уравнения представляет собой преобразование исходного уравнения к более простому уравнению, способ решения которого уже известен.
Решить уравнение – значит найти все значения неизвестных, при которых оно обращается в верное равенство, или установить, что таких значений нет.
Например, установим, является ли уравнением с одним неизвестным равенство х+0=х. Если требуется найти это неизвестное число, то рассматриваемое утверждение является уравнением. Если же рассматривать это равенство, как буквенную запись правила: при сложении любого числа с нулем получается то же самое число, то утверждение не является уравнением.
У уравнения х+0=х сколько угодно решений: любое число х является его решением. У уравнения a+3=4+a нет решений, а у уравнения a+3=4 одно решение: a=1
В определении понятия уравнение используется один из двух терминов: «переменная» или «неизвестное». Переменная — это величина, характеризующаяся множеством значений, которое она может принимать.
И.А. Моргунова, говорит о том, что уравнения имеют важное теоретическое значение, а также служат в практических целях. Большинство задач о пространственных формах и количественных отношениях реального
мира сводится к решению различных видов уравнений.
По мнению А.В. Самойловой, знакомить учащихся в начальной школе с понятием уравнения надо как можно раньше и в процессе их решения осуществлять работу по усвоению детьми правил о взаимосвязи
компонентов и результатов действий.
Математические понятия, в свою очередь, являются важнейшей неотъемлемой частью науки и учебного предмета математики. В начальном курсе математики учитель старается знакомить младших школьников с большинством понятий наглядно, путём созерцания конкретных примеров или практического оперирования ими, опираясь при этом на жизненный опыт учащихся.
В.А. Далингер, считает, что внимание должно быть направлено на умение определять понятия, а не на их заучивание. Следует правильно донести до учащихся, что научные понятия изменчивы: определение понятия – это лишь один из начальных этапов его формирования, а затем происходит процесс, который представляет собой развитие понятий, который характеризуется как постепенное уточнение и усвоение содержания и объёма понятия, его связей и отношений с другими понятиями.
Как отмечает Г.Г. Кочеткова, формирование понятия, является длительным и сложным процессом, которому следует уделять достаточное внимание в образовательном процессе. Важным этапом при формировании понятий, является усвоение его существенных признаков. Словесное определение понятия должно быть итогом работы по усвоению существенных признаков. Следует отметить, что бывает так, когда даётся словесное определение понятия, и оно сразу же используется в дальнейшей работе. Преувеличение роли при словесном определении, является одной из причин пробелов в знаниях учащихся.
Совершенно иного мнения придерживается П. Я. Гальперин, который считает, что формирование понятия не следует растягивать во времени, что это можно осуществить в один приём, когда содержание нового понятия усваивается одновременно, в полном объеме и правильном соотношении признаков, сразу применяется на всем диапазоне намеченного обобщения.
Развитие математических понятий происходит от простого к сложному, или от конкретного к обобщенному. Развитие понятий может происходить поэтапно, при этом на новом уровне обобщения, углубляющем или расширяющем содержание развиваемого понятия.
В процессе усвоения научных знаний младшие школьники сталкиваются с разными видами понятий. Формирование понятия уравнения в начальной школе подготавливает младших школьников к более успешному изучению математики в дальнейшем.
Умение решать уравнения представляет большую сложность для младших школьников. Изучение уравнений в начальных классах обладает пропедевтическим характером. В этой связи крайне важной является подготовка детей в начальных классах к более глубокому изучению уравнений в старшей школе. В начальных классах в ходе работы над уравнениями проводится закрепление правил о взаимосвязи части и целого, сторон прямоугольника и его площади, формирование вычислительных навыков и понимания связи между элементами действий, закрепление порядка действий и формирование умения решать текстовые задачи, осуществляется работа над формированием правильной математической речи. На уроках закрепления уравнения способствуют разнообразию видов заданий.
В начальных классах рассматриваются уравнения только с одной переменной.
Виды уравнений, рассматриваемых в начальных классах:
I. Простые уравнения: х – 4=6
II. Усложненные уравнения:
1. Уравнения, в которых переменная находится в правой части: 6= x-4
2. Уравнения, в которых правая часть представляет числовое выражение: х-4=36:6
3. Уравнения, в которых числовое выражение находится в обеих частях: х-(16:4)=4+2
4. Уравнения, в которых неизвестное входит в состав выражения с переменной: (х+5)-4=6
5. Уравнения, представленные комбинацией уравнений (1-4) (х+5)-4*2=36:6
6. Уравнения, в которых неизвестное находится в обеих частях 2*х-8=х+5 (только в программе Аргинской)
Проанализировав разные учебно-методические комплексы можно сделать вывод о том, что знакомство учащихся с уравнениями обычно начинается на уроках математики во 2 классе.
Автор развивающего обучения Д.Б. Эльконин, предлагают знакомить учащихся с понятием уравнение с самого начала обучения математики, но при этом, не используя взаимосвязи между компонентами и результатами арифметических действий.
http://infourok.ru/sposoby-resheniya-kvadratnyh-uravnenij-5712726.html
http://nsportal.ru/nachalnaya-shkola/matematika/2021/09/09/teoreticheskie-osnovy-formirovaniya-ponyatiya-uravneniya-v
