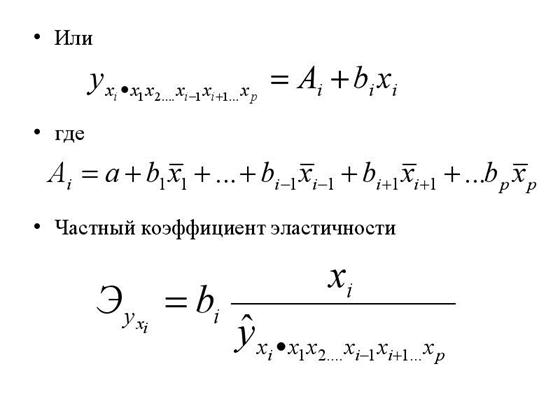На основе линейного уравнения множественной регрессии получены

Уравнение множественной регрессии

Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

• уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
• множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Отбор факторов обычно осуществляется в два этапа:

1. теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2. количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

9

13

16

14

21

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5 38 71,5 38 318 563,5 71,5 563,5 1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

73 563 1032,5

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99 0,64 -1,3 0,64 0,1 -0,0988 -1,3 -0,0988 0,14

*

73 563 1032,5

=

34,66 1,97 -2,45

Получили оценку уравнения регрессии: Y = 34.66 + 1.97X₁-2.45X₂
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 _e/∑(y_i — y_ср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X₁ (%), а также по уровню инфляции X₂ (%).

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X2	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:

1. Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
2. Рассчитать частные коэффициенты эластичности. Сделать вывод.
3. Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
5. Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.

Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

Матрица Y

7
7
7
7
7
7
8
8
8
10
9
11
9
11
12
12
12
12
14
14

Матрица X T

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619 -0,0262 -0,0183 -0,0262 0,126 -0,0338 -0,0183 -0,0338 0,0102

=

0,222 -0,00939 -0,00654 -0,00939 0,0452 -0,0121 -0,00654 -0,0121 0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x₁, x₂, x₃ взятых по отдельности. Для каждой объясняющей переменной:

1. Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
2. Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации.
3. Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
4. Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
5. Постройте диаграмму остатков.
6. Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение F_табл определите с помощью функции FРАСПОБР).
7. Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
8. Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
9. Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
10. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

На основе линейного уравнения множественной регрессии

Дата добавления: 2014-11-28 ; просмотров: 6342 ; Нарушение авторских прав

· На основе линейного уравнения множественной регрессии

· могут быть найдены частные уравнения регрессии

· Частные уравнения регрессии имеют следующий вид:

· Или

· где

· Частный коэффициент эластичности

· В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, т.к. другие факторы закреплены на неизменном уровне.

· 18 1. Основная цель множественнойрегрессии – построить модель с большимчислом факторов, определив при этомвлияние каждого из них в отдельности, атакже совокупное их воздействие намоделируемый показатель.

· 2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи> Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.> спецификации модели: отбор факторов и выбор вида уравнения регрессии.>2.

· Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной> Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.> Включение в модель факторов с высокой интеркорреляцией (т.е. корреляции между объясняющими переменными), может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.>3.

· Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор не улучшает модель и практически является лишним фактором.> и .> При дополнительном включении в регрессию m фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:> Если строится модель с набором m факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как с соответствующей остаточной дисперсией .>4.

· Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии> Поэтому отбор факторов осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии.> Насыщение модели лишними факторами не снижает величину остаточной дисперсии и не увеличивает показатель детерминации и приводит к статистической незначимости параметров регрессии по критерию Стьюдента>5.

· Пусть, например, при изучении зависимости матрица парных коэффициентов корреляции оказалась следующей:Очевидно, что факторы х1 и х2 дублируют друг друга. В анализ целесообразно включить фактор х2, а не х1. Поэтому в данном случае в уравнение множественной регрессии включаются факторы х2, х3.>6.

· По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности.>7.

· Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.> Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.> Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл.> Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:>8.

· Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.> Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.>9.

· Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по F- критерию Фишера> Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если , то возможно построение следующего совмещенного уравнения:>10.

· При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а -критерий меньше табличного значения.> Шаговый регрессионный анализ – исключение ранее введенного фактора.> Метод включения – дополнительное введение фактора.> Метод исключения – отсев факторов из полного его набора.> Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:> Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.>11.

· Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна: (2.2)> Рассмотрим линейную модель множественной регрессии (2.1)>12.

· Находим частные производные первого порядка:> Итак. Имеем функцию аргумента:> Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.>13.

· где – стандартизированные переменные: , , для которых среднее значение равно нулю: , а среднее квадратическое отклонение равно единице: ; – стандартизированные коэффициенты регрессии.> Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:>14.

· Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.>15.

· Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии следующим образом:> где и – коэффициенты парной и межфакторной корреляции.> Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида (2.5)>16.

· т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:> могут быть найдены частные уравнения регрессии: (2.8)> (2.7)> На основе линейного уравнения множественной регрессии> Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением .>17.

· В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:>18.

· которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.> Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: (2.11)> где –коэффициент регрессии для фактора в уравнении множественной регрессии, – частное уравнение регрессии.>19.

· Для удобства дальнейших вычислений составляем таблицу ( ):> Предполагая, что между переменными y , , существует линейная корреляционная зависимость, найдем уравнение регрессии y по и .> Рассмотрим пример (для сокращения объема вычислений ограничимся только десятью наблюдениями). Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего y (т), мощности пласта (м) и уровне механизации работ (%), характеризующие процесс добычи угля в 10 шахтах.>20.

· Оно показывает, что при увеличении только мощности пласта (при неизменном ) на 1 м добыча угля на одного рабочего y увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ (при неизменном ) на 1% – в среднем на 0,367 т.> Откуда получаем, что . Т.е. получили следующее уравнение множественной регрессии:> Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:>21.

· Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что мощность пласта оказывает большее влияние на сменную добычу угля, чем уровень механизации работ.> Т.е. уравнение будет выглядеть следующим образом:> при этом стандартизованные коэффициенты регрессии будут> Найдем уравнение множественной регрессии в стандартизованном масштабе:>22.

· Т.е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат y фактора , чем фактора .> Вычисляем:> Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):>23.

17ножественная регрессия. Проблемы спецификации модели: отбор факторов при построении множественной регрессии; выбор формы уравнения регрессии

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики.

В настоящее время множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, который в свою очередь включает 2 круга вопросов: отбор факторов и выбор уравнения регрессии. Отбор факторов обычно осуществляется в два этапа: 1) теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;

2) количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции): ry , y ry , x1 ryx2 . ry , xm rx 1, y rx1, x2 rx2x 2 . rx 2, xm . rxm , y rxm, x1 rxm , x2 . rxm , xm где ry , xj — линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками y и хj j=1;m , m -число факторов. rxj , xk — линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками хj и хk j,k =1;m. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов). 2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).

3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами. Мультиколлинеарность может привести к нежелательным последствиям: 1) оценки параметров становятся ненадежными. Они обнаруживают большие стандартные ошибки. С изменением объема наблюдений оценки меняются (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

2) затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл; 3) становится невозможным определить изолированное влияние факторов на результативный показатель.

Мультиколлинеарность имеет место, если определитель матрицы межфакторной корреляции близок к нулю:

Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет. Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них — исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, теоретический коэффициент детерминации -R2y(x1. xm) снизится несущественно).

Определение факторов, ответственных за мультиколлинеарность, может быть основано на анализе матрицы межфакторной корреляции. При этом определяют пару признаков-факторов, которые сильнее всего связаны между собой (коэффициент линейной парной корреляции максимален по модулю). Из этой пары в наибольшей степени ответственным за мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели (имеет более высокие по модулю значения коэффициентов парной линейной корреляции).

Еще один способ определения факторов, ответственных за мультиколлинеарность основан на вычислении коэффициентов множественной детерминации (R2xj(x1. xj-1,xj+1. xm)), показывающего зависимость фактора xj от других факторов модели x1. xj-1, x j+1. xm. Чем ближе значение коэффициента множественной детерминации к единице, тем больше ответственность за мультиколлинеарность фактора, выступающего в роли зависимой переменной. Сравнивая между собой коэффициенты множественной детерминации для различных факторов можно проранжировать переменные по степени ответственности за мультиколлинеарность. При выборе формы уравнения множественной регрессии предпочтение отдается линейной функции:

yi =a+b1·x1i+ b2·x2i+. + bm·xmi+ui

в виду четкой интерпретации параметров.

Данное уравнение регрессии называют уравнением регрессии в естественном (натуральном) масштабе. Коэффициент регрессии bj при факторе хj называют условно-чистым коэффициентом регрессии. Он измеряет среднее по совокупности отклонение признака-результата от его средней величины при отклонении признака-фактора хj на единицу, при условии, что все прочие факторы модели не изменяются (зафиксированы на своих средних уровнях).

Если не делать предположения о значениях прочих факторов, входящих в модель, то это означало бы, что каждый из них при изменении х j также изменялся бы (так как факторы связаны между собой), и своими изменениями оказывали бы влияние на признак-результат.

Если оцененную модель регрессии предполагается использовать для изучения экономических связей, то устранение мультиколлинеарных факторов является обязательным, потому что их наличие в модели может привести к неправильным знакам коэффициентов регрессии. При построении прогноза на основе модели регрессии с мультиколлинеарными факторами необходимо оценивать ситуацию по величине ошибки прогноза. Если её величина является удовлетворительной, то модель можно использовать, несмотря на мультиколлинеарность. Если же величина ошибки прогноза большая, то устранение мультиколлинеарных факторов из модели регрессии является одним из методов повышения точности прогноза. К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся: 1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна; 2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы: lny=β0+β1lnx1+β2lnx2+ε. Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов; Если рассмотренные способы не помогли устранить мультиколлинеарность факторов, то переходят к использованию смещённых методов оценки неизвестных параметров модели регрессии, или методов исключения переменных из модели множественной регрессии. Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж(ridge). При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число τ: 10-6 ‹ τ ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле: где ln – единичная матрица. Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу. Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии. Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода заключается в сокращении числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных xi (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F. При этом выдвигается требование, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех факторных переменных xi (i=0,…,n), второй компоненте – максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д. Метод пошагового включения переменных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную. Метод пошагового включения осуществляется по следующему алгоритму: 1) из всех факторных переменных в модель регрессии включаются те переменные, которым соответствует наибольший модуль линейного коэффициента парной корреляции с результативной переменной; 2) при добавлении в модель регрессии новых факторных переменных проверяется их значимость с помощью F-критерия Фишера. При том выдвигается основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии. Обратная гипотеза состоит в утверждении о целесообразности включения факторной переменной xk в модель множественной регрессии. Критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров. Наблюдаемое значение F-критерия рассчитывается по формуле: где q – число уже включённых в модель регрессии факторных переменных. При проверке основной гипотезы возможны следующие ситуации. Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии отвергается. Следовательно, включение данной переменной в модель множественной регрессии является обоснованным. Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≤Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии принимается. Следовательно, данную факторную переменную можно не включать в модель без ущерба для её качества 3) проверка факторных переменных на значимость осуществляется до тех пор, пока не найдётся хотя бы одна переменная, для которой не выполняется условие Fнабл›Fкрит.

15 10.2. Отбор факторов при построении множественной регрессии

Включение в уравнение множественной регрессии того иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями.

Факторы, включаемые множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: они могут быть проранжированы).

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Так, в уравнении у = а + b₁ x₁ + b₂ х₂ +ε предполагается, что факторы x₁, и х₂ независимы друг от друга, т. е. r_x1x2 = 0. Тогда можно говорить, что параметр b₁ измеряет силу влияния фактора х₁, на результат у при неизменном значении фактора ₂.

Если же r_x1x2 = 1, то с изменением фактора x₁, фактор х₂ не может оставаться неизменным. Отсюда b₁ и b₂ нельзя интерпретировать как показатели раздельного влияния x₁, и х₂ и на у.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается коэффициент детерминации R 2 , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других не учтенных в модели факторов оценивается как 1 — R 2 с соответствующей остаточной дисперсией S 2 .

При дополнительном включении в регрессию (р +1)-го фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться.

Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ факторхр + 1 не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости.

Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессииу = а + b₁ x₁ + b₂ х₂ + . + bр • х_р параметры при х называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

• метод исключения;
• метод включения;
• шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения.

11 Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительного изменения экономического фактора, от которого он зависит при неизменных остальных влияющих на него факторов.

Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.

Формула для расчета коэффициента эластичности имеет вид:

Обычно рассчитывается средний коэффициент эластичности: .

Формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:

Вид функции, y	Первая производная, y’	Средний коэффициент эластичности,
	b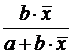
	b1+2b2x

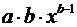Несмотря на широкое применения в эконометрике коэффициентов эластичности, возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.

Множественная линейная регрессия. Улучшение модели регрессии

Понятие множественной линейной регрессии

Множественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными.

В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель

,

где — коэффициенты функции линейной регрессии генеральной совокупности,

— случайная ошибка.

Функция множественной линейной регрессии для выборки имеет следующий вид:

,

где — коэффициенты модели регрессии выборки,

— ошибка.

Уравнение множественной линейной регрессии и метод наименьших квадратов

Коэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов.

Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах.

МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде

Метод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений

Решение системы можно получить, например, методом Крамера:

.

Определитель системы записывается так:

МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде

Данные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц:

Формула коэффициентов множественной линейной регрессии в матричном виде следующая:

,

где — матрица, транспонированная к матрице X,

— матрица, обратная к матрице .

Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов.

Построение наилучшей (наиболее качественной) модели множественной линейной регрессии

Пусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её.

Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации , F-статистика (статистика Фишера), сумма квадратов остатков RSS, стандартная ошибка регрессии (SEE). В случае множественной регрессии следует использовать также скорректированный коэффициент детерминации (adjusted ), который применяется при исключении или добавлении в модель наблюдений или переменных.

Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:

• условие 1: математическое ожидание остатков равно нулю для всех наблюдений ( ε(e i ) = 0 );
• условие 2: теоретическая дисперсия остатков постоянна (равна константе) для всех наблюдений ( σ²(e i ) = σ²(e i ), i = 1, . n );
• условие 3: отсутствие систематической связи между остатками в любых двух наблюдениях;
• условие 4: отсутствие зависимости между остатками и объясняющими (независимыми) переменными.

В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является

Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента.

В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному.

В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах.

Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE).

Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере.

Оценка качества модели множественной линейной регрессии в целом

Пример. Задание 1. Получено следующее уравнение множественной линейной регрессии:

и следующие показатели качества описываемой этим уравнением модели:

	adj.	RSS	SEE	F	p-level
0,426	0,279	2,835	1,684	2,892	0,008

Сделать вывод о качестве модели в целом.

Ответ. По всем показателям модель некачественная. Значение не стремится к единице, а значение скорректированного ещё более низкое. Значение RSS, напротив, высокое, а p-level — низкое.

Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши):

Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной.

Анализ значимости коэффициентов модели множественной линейной регрессии

С помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05.

Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:

Перем.	Знач. коэф.	t	p-level
X1	0,129	2,386	0,022
X2	-0,286	-2,439	0,019
X3	-0,037	-0,238	0,813
X4	0,15	1,928	0,061
X5	0,328	0,548	0,587
X6	-0,391	-0,503	0,618
X7	-0,673	-0,898	0,375
X8	-0,006	-0,07	0,944
X9	-1,937	-2,794	0,008
X10	-1,233	-1,863	0,07

Сделать вывод о значимости коэффициентов модели.

Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента.

Исключение резко выделяющихся наблюдений

Пример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.

№	adj.	SEE	F	p- level	незнач. пер.
10	0,411	2,55	2,655	0,015	X3, X4, X5, X6, X7, X8, X10
3	0,21	2,58	2,249	0,036	X3, X4, X5, X6, X7, X8, X10
4	0,16	2,61	1,878	0,082	X3, X4, X5, X6, X7, X8, X10

Уравнение конечной множественной линейной регрессии:

Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться.

Исключение незначимых переменных из модели

Пример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.

Искл. пер.	adj.	SEE	F	p- level	*
X3	0,18	1,71	2,119	0,053	X4, X5, X6, X7, X8, X10
X4	0,145	1,745	1,974	0,077	X5, X6, X7, X8, X10
X5	0,163	2,368	2,282	0,048	X6, X7, X8, X10
X6	0,171	2,355	2,586	0,033	X7, X8, X10
X7	0,167	2,223	2,842	0,027	X8, X10
X8	0,184	1,705	3,599	0,013	X10

Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы.

Уравнение конечной множественной линейной регрессии после исключения незначимых переменных:

Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически».

Нелинейные модели для сравнения

Пример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных.

Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2.

Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных:

Показатели качества первой модели нелинейной регрессии:

	adj.	RSS	SEE	F	p-level
0,17	0,134	159,9	1,845	4,8	0,0127

Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.

Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных:

Показатели качества второй модели нелинейной регрессии:

	adj.	RSS	SEE	F	p-level
0,182	0,148	157,431	1,83	5,245	0

Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.

Применение пошаговых алгоритмов включения и исключения переменных

Пример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:

• в окне Tolerance необходимо установить критическое значение для уровня толерантности (оставить предложенное по умолчанию);
• в окне F-remove необходимо установить критическое значение для статистики исключения (оставить предложенное по умолчанию);
• в окне Display Results необходимо установить режим At each step (результаты выводятся на каждом шаге процедуры).

Построить, как описано выше, модели множественной линейной регрессии автоматически.

В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии:

Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:

	adj.	RSS	SEE	F	p-level
0,41	0,343	113,67	1,61	6,11	0,002

В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии:

Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:

	adj.	RSS	SEE	F	p-level
0,22	0,186	150,28	1,79	6,61	0

Выбор самой качественной модели множественной линейной регрессии

Пример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.

Модель	Ручная	Кв. перем.	Лог. перем.	forward stepwise	backward stepwise
	0,255	0,17	0,182	0,41	0,22
adj.	0,184	0,134	0,148	0,343	0,186
RSS	122,01	159,9	157,43	113,67	150,28
SEE	1,705	1,845	1,83	1,61	1,79
F	3,599	4,8	5,245	6,11	6,61
p-level	0,013	0,0127	0	0,002	0

Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей.