На рисунке изображен график функции уравнение касательной

Задания по теме «Геометрический смысл производной. Касательная к графику функции»

Открытый банк заданий по теме геометрический смысл производной. Задания B7 из ЕГЭ по математике (профильный уровень)

Задание №1165

Условие

Прямая y=3x+2 является касательной к графику функции y=-12x^2+bx-10. Найдите b , учитывая, что абсцисса точки касания меньше нуля.

Решение

Пусть x_0 — абсцисса точки на графике функции y=-12x^2+bx-10, через которую проходит касательная к этому графику.

Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=-24x_0+b=3. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть -12x_0^2+bx_0-10=3x_0+2. Получаем систему уравнений \begin -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end

Решая эту систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания меньше нуля, поэтому x_0=-1, тогда b=3+24x_0=-21.

Ответ

Задание №1160

Условие

Прямая y=-3x+4 параллельна касательной к графику функции y=-x^2+5x-7. Найдите абсциссу точки касания.

Решение

Угловой коэффициент прямой к графику функции y=-x^2+5x-7 в произвольной точке x_0 равен y'(x_0). Но y’=-2x+5, значит, y'(x_0)=-2x_0+5. Угловой коэффициент прямой y=-3x+4, указанной в условии, равен -3. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что =-2x_0 +5=-3.

Получаем: x_0 = 4.

Ответ

Задание №1157

Условие

На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.

Решение

По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через \alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \pi -\alpha, который является тупым.

Как известно, tg(\pi -\alpha) и будет значением производной функции f(x) в точке x_0. Заметим, что tg \alpha =\frac=\frac<2-1><-1-(-6)>=\frac15. Отсюда по формулам приведения получаем: tg(\pi -\alpha ) =-tg \alpha =-\frac15=-0,2.

Ответ

Задание №1156

Условие

Прямая y=-2x-4 является касательной к графику функции y=16x^2+bx+12. Найдите b , учитывая, что абсцисса точки касания больше нуля.

Решение

Пусть x_0 — абсцисса точки на графике функции y=16x^2+bx+12, через которую

проходит касательная к этому графику.

Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=32x_0+b=-2. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть 16x_0^2+bx_0+12=-2x_0-4. Получаем систему уравнений \begin 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end

Решая систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1, тогда b=-2-32x_0=-34.

Ответ

Задание №1152

Условие

На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых касательная к графику функции параллельна прямой y=6.

Решение

Прямая y=6 параллельна оси Ox . Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 4 .

Ответ

Задание №1151

Условие

Прямая y=4x-6 параллельна касательной к графику функции y=x^2-4x+9. Найдите абсциссу точки касания.

Решение

Угловой коэффициент касательной к графику функции y=x^2-4x+9 в произвольной точке x_0 равен y'(x_0). Но y’=2x-4, значит, y'(x_0)=2x_0-4. Угловой коэффициент касательной y=4x-7, указанной в условии, равен 4 . Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что 2x_0-4=4. Получаем: x_0=4.

Ответ

Задание №1147

Условие

На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.

Решение

По рисунку определяем, что касательная проходит через точки A(1; 1) и B(5; 4). Обозначим через C(5; 1) точку пересечения прямых x=5 и y=1, а через \alpha угол BAC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \alpha.

Как известно, tg \alpha и будет значением производной функции f(x) в точке x_0.

Заметим, что tg \alpha =\frac=\frac34=0,75.

Ответ

Задание №1145

Условие

Прямая y=-2x-8 является касательной к графику функции y=x^3+3x^2-11x-3. Найдите абсциссу точки касания.

Решение

Угловой коэффициент касательной к графику функции y=x^3+3x^2-11x-3 в произвольной точке x_0 равен y'(x_0). Но y’=3x^2+6x-11, значит y'(x_0)=3x_0^2+6x_0-11. Угловой коэффициент касательной y=-2x-8, указанной в условии равен -2. Поэтому находим такое значение x_0, что 3x_0^2+6x_0-11=-2, 3x_0^2+6x_0-9=0. По формулам корней квадратного уравнения получаем, что либо x_0=-3, либо x_0=1.

Заметим, что y(-3)= (-3)^3+3\cdot (-3)^2-11\cdot (-3)-3= 30, а y(1)= 1^3+3\cdot 1^2-11\cdot 1-3= -10. Получаем две возможные точки касания: (-3; 30); (1; -10). Выясним, через какую из них проходит касательная y=2x-8. Координаты точки (-3; 30) не удовлетворяют уравнению касательной, так как равенство 30=-2\cdot (-3)-8 не является верным. Но равенство -10=(-2)\cdot 1-8 является верным. Поэтому касательная проходит через точку (1, -10) с абсциссой, равной 1.

Ответ

Задание №1144

Условие

Прямая y=-2x+5 является касательной к графику функции y=ax^2+2x+7. Найдите a .

Решение

Пусть (x_0; y_0) — точка, в которой прямая y=-2x+5 касается графика функции y=ax^2+2x+7. Тогда угловой коэффициент касательной к графику функции y=ax^2+2x+7 в точке x_0 равен y'(x_0). Но y’=2ax+2, значит y'(x_0)=2ax_0+2.

Угловой коэффициент касательной y=-2x+5, указанной в условии, равен -2. Поэтому 2ax_0+2=-2. Отсюда, a \neq 0.

Кроме того точка (x_0; y_0) лежит на прямой y=-2x+5 и на графике функции y=ax^2+2x+7. Значит, выполняется равенство y_0=-2x_0+5=ax_0^2+2x_0+7. Получаем систему:

\begin 2ax_0+2=-2, \\ -2x_0+5=ax_0^2+2x_0+7; \end

\begin x_0=-\frac2a, \\ ax_0^2+4x_0+2=0; \end

Ответ

Задание №1141

Условие

На рисунке изображён график y=f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.

Решение

Пусть x_0 — абсцисса точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней. Тогда значение производной y=f'(x) в точке x_0 равно 0 , так как угловой коэффициент оси абсцисс y=0 равен 0 .

Но из графика видно, что f'(x)=0 в единственной точке x_0=-5.

Действительно, прямая y=0 пересекает график функции y=f'(x) в единственной точке (-5; 0), абсцисса которой равна -5.

Задача 3146 На рисунке изображены график функции.

Условие

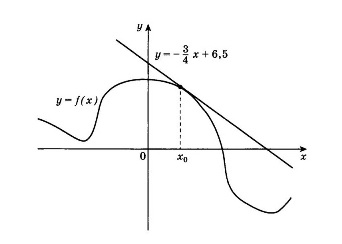
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. найдите значение производной функции y=4*f(x)-3 в точке x0.

Решение

Нужно найти производную функции y= 4f(x)-3 в точке Х0.

То есть у′ = (4f(x)-3)′ = 4f′(х) — 0 = 4f′(x) в точке Х0.

Вспомним, что f′(х0) равно коэффициенту при х в уравнении касательной у = (-3/4)х + 6,5 к графику функции f(x) в точке х0.

Значит f(x0) = -3/4. Подставим это значение в у′:

у′ = 4f′(x0) = 4 * (-3/4) = -3 — это и есть искомое значение производной функции y= 4f(x)-3 в точке Х0.

Задание 6 ЕГЭ по математике (профиль)

Открытый банк заданий mathege.ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege.ru.

Использование свойств производной для исследования функций

27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.

27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.

27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).

27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?

27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?

27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].

27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].

27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].

27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].

119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.

317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. В скольких из этих точек производная функции f(x) положительна?

317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂. В скольких из этих точек производная функции f(x) отрицательна?

317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. Сколько из этих точек лежит на промежутках возрастания функции f(x)?

317542. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. Сколько из этих точек лежит на промежутках убывания функции f(x)?

Геометрический смысл производной

27485. Прямая y = 7x — 5 параллельна касательной к графику функции y = x 2 + 6x — 8. Найдите абсциссу точки касания.

27486. Прямая y = -4x — 11 является касательной к графику функции y = x 3 + 7x 2 + 7x — 6. Найдите абсциссу точки касания.

27489. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.

27501. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.

27503. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

27504. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

27505. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

27506. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

40130. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x — 2 или совпадает с ней.

40131. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.

119972. Прямая y = 3x +1 является касательной к графику функции ax 2 + 2x + 3. Найдите a.

119973. Прямая y = -5x + 8 является касательной к графику функции 28x 2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.

119974. Прямая y = 3x + 4 является касательной к графику функции 3x 2 — 3x + c. Найдите c.

317543. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

317544. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

[s60u_expand more_text=»Ответ» less_text=»Свернуть» height=»1″ hide_less=»no» text_color=»#333333″ link_color=»#0088FF» link_style=»default» link_align=»left» more_icon=»» less_icon=»» /> [/su_expand]

Физический смысл производной

119975. Материальная точка движется прямолинейно по закону x(t) = 6t 2 — 48t +17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 с.

119976. Материальная точка движется прямолинейно по закону x(t) = 1/2t 3 — 3t 2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.

119977. Материальная точка движется прямолинейно по закону x(t) = -t 4 + 6t 3 + 5t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.

119978. Материальная точка движется прямолинейно по закону x(t) = t 2 -13t +23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?

119979. Материальная точка движется прямолинейно по закону x(t) = 1/3t 3 — 3t 2 — 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Первообразная

323077. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].

323078. На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).

323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x 3 + 30x 2 + 302x — 15/8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x)= -x 3 — 27x 2 — 240x — 8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.