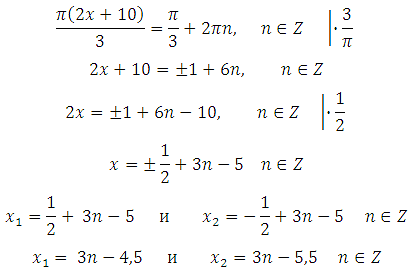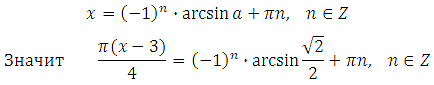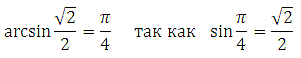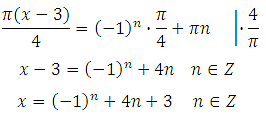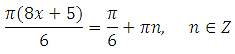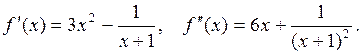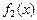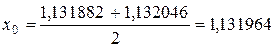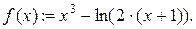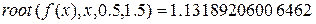Нахождение наименьшего положительного корня уравнения

Тригонометрические уравнения

Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

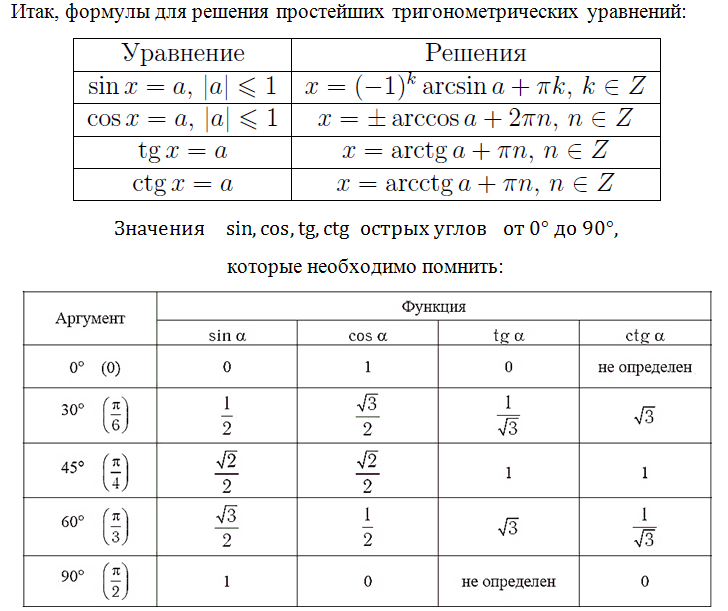
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.

При n = – 2 х₁= 3 (– 2) – 4,5 = – 10,5 х₂= 3 (– 2) – 5,5 = – 11,5

При n = – 1 х₁= 3 (– 1) – 4,5 = – 7,5 х₂= 3 (– 1) – 5,5 = – 8,5

При n = 0 х₁= 3∙0 – 4,5 = – 4,5 х₂= 3∙0 – 5,5 = – 5,5

При n = 1 х₁= 3∙1 – 4,5 = – 1,5 х₂= 3∙1 – 5,5 = – 2,5

При n = 2 х₁= 3∙2 – 4,5 = 1,5 х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен –1,5

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …

При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4

При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6

При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12

Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.

Выразим x (умножим обе части уравнения на 6 и разделим на Пи):

Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

Спасибо за внимание, учитесь с удовольствием!

Нахождение наименьшего положительного корня.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема урока: Нахождение наименьшего положительного корня.

— актуализировать знания учащихся по теме «Решение тригонометрических уравнений» и обеспечить их применение при решении задач вариантов ЕНТ;

— рассмотреть общие подходы решения тригонометрических уравнений;

— закрепить навыки решения тригонометрических уравнений;

— познакомить с новыми способами решения тригонометрических уравнений.

— содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;

— формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;

— вырабатывать внимание, самостоятельность при работе на уроке;

— способствовать формированию активности и настойчивости, максимальной работоспособности.

II .Устная работа . Решите уравнения:

а) ; в) ;

б) ; г) .

а) ; в) ;

б) ; г) .

а) ; в) ;

б) ; г) .

а) ; в) ;

III . Работа по отработке умений решать тригонометрические уравнения (работа у доски и в тетрадях )

Найти корни заданного уравнения на заданном промежутке:

а) .

. Однако для решения нашего уравнения данная запись формулы для нахождения корней тригонометрического уравнения не является удобной, поэтому воспользуемся другой записью:

Нетрудно видеть, что простым перебором по параметру n мы сразу получаем все требуемые корни уравнения, т.е.:

Ответ: .

1.Решите уравнение и найдите. Наименьший положительный корень;

2. Найти наименьший положительный корень уравнения sinx + sin 5 x = 0.

3.Найдите наименьший положительный корень уравнения cosx + cos 5 x = 0

А. π/6 В. π/4 Б. π/2 Г. π

4. Из Абитуриента №26 Найдите наименьшее решение уравнения sinx = в интервале [ 500 ;760]

5. Найдите наименьшее решение уравнения cos = в интервале [750;1050] (780 0 )

Пример выполнения работы. Найти наименьший положительный корень уравнения

Найти наименьший положительный корень уравнения

.

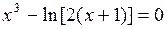
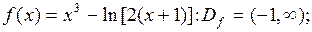
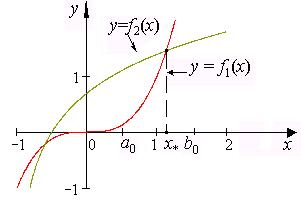
1. Область определения функции ее производные

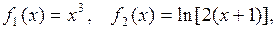
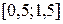
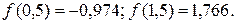
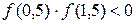
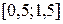
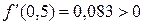
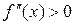
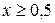
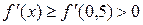
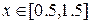
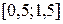
2. Строим графики функций: находим точки пересечения графиков. Из рис. 2.6 видно, что наименьший положительный корень данного уравнения лежит внутри отрезка . Проверим аналитически, что корень отделен на этом отрезке. Вычисляем: Поскольку и функция непрерывна, то в силу теоремы 1 внутри отрезка имеются корни. Поскольку и для всех , следовательно для всех , т. е. функция возрастающая на . Поэтому на основании теоремы 2 внутри этого отрезка имеется один корень уравнения и он может быть взят в качестве начального.

Рис. 2.6. Графики функций 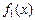и

3. С помощью микрокалькулятора делаем 3 шага методом половинного деления; результаты заносим в табл. 2.2.

Таблица 2.2

Уточнение начального отрезка методом половинного деления

N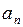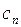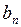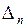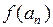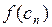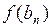
0,5	1,0	1,5	1,0	– 0,974	– 0,386	1,766
1,0	1,25	1,5	0,5	– 0,386	0,449	1,766
1,0	1,125	1,25	0,25	– 0,386	– 0,023	0,449
1,125	1,1875	1,25	0,125

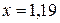
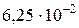
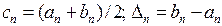
В результате получаем: уточненный отрезок [1,125; 1,250]; приближенное значение корня ; погрешность корня равной . При этом были введены следующие дополнительные обозначения: .

Дальнейшее уточнение корня проводим комбинированным методом. Так как 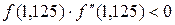, то левый конец отрезка [1,125; 1,250] уточняем методом хорд, а правый – методом Ньютона. Поэтому используем формулы (2.13). Результаты вычислений заносим в табл. 2.3.

Таблица 2.3

Уточнение корня комбинированным методом

N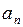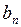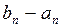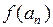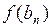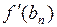
1,125	1,250	0,125	– 0,023092	0,444045	4,243056
1,131114	1,144170	0,013056	– 0,002622	0,041961	3,460994
1,131882	1,132046	0,000164

Так как 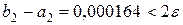, вычисления прекращаем на втором шаге. Находим корень уравнения

4. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab2.mcd. Вводим функцию

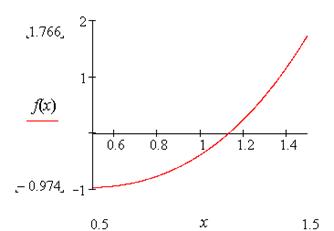
Строим график функции на найденном начальном интервале [0,5;1,5] (рис. 2.7)

Рис. 2.7. График функции f(x)

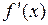
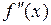
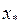
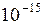
Характеристики графика свидетельствуют, что функция непрерывна, и существуют и знакопостоянны на этом отрезке (т. е. функция монотонна и не меняет направление выпуклости) и что корень уравнения лежит в интервале [0,5;1,5], причем единственный. Таким образом, можем применить все вышеперечисленные методы. После этого находим корень с точностью до с помощью встроенной функции системы Mathcad

5. Выписываем точное решение 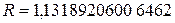и сравниваем полученные результаты ручного и машинного счета. Определяем погрешность:

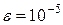
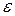
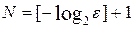
6. Определяем с помощью компьютера значение корня методом половинного деления с точностью . По формуле, чтобы удовлетворить погрешности , для начального отрезка единичной длины необходимо провести шагов.

Выписываем автоматически вычисленное по этой формуле в соответствующем разделе количество шагов 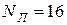и таблицу 2.4, содержащую первые и последние три шага получившейся матрицы приближений корня методом половинного деления.

Таблица 2.4

Отыскание корня методом половинного деления

N	…
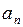	0,5	1,0	1,0	1,125	…	1,131836	1,131866	1,131882
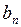	1,5	1,5	1,25	1,25	…	1,131897	1,131897	1,131897

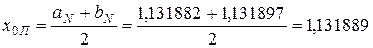
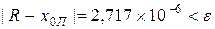
Получим корень , абсолютная погрешность которого .

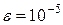
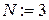
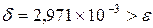
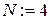
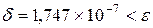
7. Получим на компьютере значение корня методом Ньютона с точностью . Для этого вводим в начале соответсвующего раздела и с помощью запрограммированной формулы (2.7) определяем погрешность . Следовательно, увеличивая N на единицу, вводим в программу и получаем . То есть требуемая точность достигнута (если это не так продолжаем увеличивать N на единицу).

. Выписываем получившуюся таблицу 2.5 для .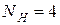

Таблица 2.5

Отыскание корня методом Ньютона

N
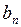	1,5	1,221958726	1,139300286	1,131948438	1,131892063

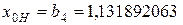
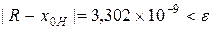
Получим приближенный корень , абсолютная погрешность которого .

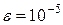
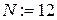
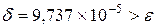
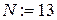
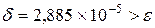
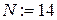
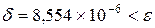
8. Вычисляем на компьютере значение корня методом хорд с точностью . Для этого вводим в начале соответсвующего раздела и с помощью запрограммированной формулы (2.10) получим и оценим погрешность . Следовательно, увеличиваем N на единицу, вводим , для которого . Увеличиваем N еще на единицу, вводим , для которого . Т. е. требуемая точность достигнута (если это не так, продолжаем увеличивать N на единицу).

Выписываем первые и последние два шага из получившейся таблицы для .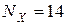

Таблица 2.6

Отыскание корня методом хорд

N	…
	0,5	0,855440054	1,035664929	…	1,131891898	1,131892012

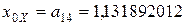
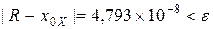
Получим корень , абсолютная погрешность которого .

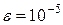
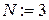
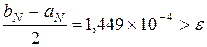
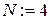
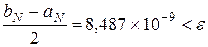
9. Вычисляем на компьютере значение корня комбинированным методом с точностью . Для этого вводим в начале соответсвующего раздела и получаем по формуле (2.13) погрешность . Следовательно, увеличиваем N на единицу и вводим , для которого . То есть требуемая точность достигнута (если это не так, продолжаем увеличивать N на единицу).

Выписываем получившуюся таблицу 2.7 для .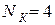

Таблица 2.7

Отыскание корня комбинированным методом

N
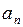	0,5	0,8554400542	1,1020813008	1,1316586589	1,1318920464
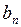	1,5	1,2219587264	1,1393002857	1,1319483820	1,1318920634

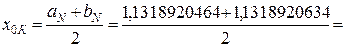
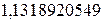
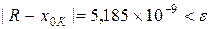
Получим корень , абсолютная погрешность которого .

10. Все расчеты оформляются в виде отчета по лабораторной работе.

Вопросы для самоконтроля

1. Уравнение какого типа решается в данной работе?

2. Что называется корнем уравнения ?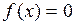

3. Как графически решить уравнения ?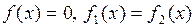

4. Перечислите достоинства и недостатки графического метода.

5. В чем состоит этап отделения корней уравнения ?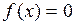

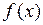
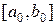
6. Сколько корней должна иметь функция на начальном отрезке ?

7. Как определить аналитически: возрастает или убывает функция на промежутке?

8. Как определить аналитически: выпукла или вогнута функция на промежутке?

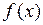
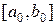
9. Какие условия, наложенные на , гарантируют наличие хотя бы одного корня уравнения на начальном отрезке ?

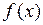
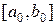
10. Какие условия, наложенные на , гарантируют наличие не более одного корня уравнения на начальном отрезке ?

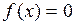
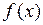
11. Привести алгоритм решения уравнения методом половинного деления. Какие условия при этом должны быть наложены на функцию ?

12. Какие условия должны быть наложены на 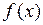, чтобы уравнение можно было решить методом Ньютона?

13. Как выбирается начальная точка 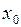в методе Ньютона?

14. Вывести формулу для вычисления последовательных приближений методом Ньютона, записать формулу оценки погрешности.

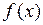
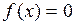
15. Какие условия должны быть наложены на , чтобы уравнение можно было решить методом хорд?

16. Как выбирается начальная точка 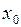в методе хорд?

17. Вывести формулу для вычисления n последовательных приближений методом хорд, записать формулу оценки погрешности.

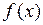
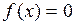
18. Какие условия должны быть наложены на , чтобы уравнение можно было решить комбинированным методом?

19. Выписать формулы, по которым уточняются концы начального отрезка 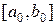комбинированным методом. В зависимости от каких условий осуществляется выбор формул?

20. Указать условие, по которому процесс уточнения отрезка комбинированным методом должен быть прерван? Как затем найти корень?