Написать каноническое уравнение симметричного относительно

Канонические уравнения прямой в пространстве: теория, примеры, решение задач

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

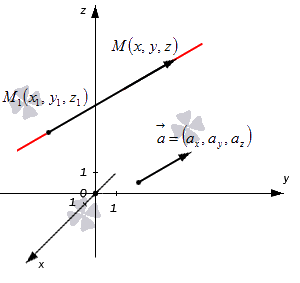
Допустим, у нас есть прямоугольная система координат O x y z , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a , а точку M , то можно записать, что M 1 ( x 1 , y 1 , z 1 ) лежит на прямой a и направляющим вектором этой прямой будет a → = ( a x , a y , a z ) . Чтобы множество точек M ( x , y , z ) определяло прямую a , векторы M 1 M → и a → должны быть коллинеарными,

Если мы знаем координаты векторов M 1 M → и a → , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a → . Для того чтобы получить координаты M 1 M → , нам необходимо вычислить разность между M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) . Запишем:

M 1 M → = x — x 1 , y — y 1 , z — z 1

После этого нужное нам условие мы можем сформулировать так: M 1 M → = x — x 1 , y — y 1 , z — z 1 и a → = ( a x , a y , a z ) : M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z

Здесь значением переменной λ может быть любое действительное число или ноль. Если λ = 0 , то M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) совпадут, что не противоречит нашим рассуждениям.

При значениях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 мы можем разрешить относительно параметра λ все уравнения системы x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z

Между правыми частями после этого можно будет поставить знак равенства:

x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

В итоге у нас получились уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров a x , a y , a z , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0 , поскольку направляющий вектор a → = ( a x , a y , a z ) нулевым не бывает.

Если один-два параметра a равны 0 , то уравнение x — x 1 a x = y — y 1 a y = z — z 1 a z носит условный характер. Его следует считать равным следующей записи:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , то канонические уравнения примут следующий вид:

x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 2 a x = y — y 2 a y = z — z 2 a z .

2) поскольку a → = ( a x , a y , a z ) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тогда прямая может быть определена с помощью уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 1 μ · a x = y — y 1 μ · a y = z — z 1 μ · a z .

Вот несколько примеров таких уравнений с заданными значениями:

x — 3 2 = y + 1 — 1 2 = z ln 7

Тут x 1 = 3 , y 1 = — 1 , z 1 = 0 , a x = 2 , a y = — 1 2 , a z = ln 7 .

x — 4 0 = y + 2 1 = z + 1 0

Тут M 1 ( 4 , — 2 , — 1 ) , a → = ( 0 , 1 , 0 ) .

Как составить каноническое уравнение прямой в пространстве

Мы выяснили, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z будут соответствовать прямой, проходящей через точку M 1 ( x 1 , y 1 , z 1 ) , а вектор a → = ( a x , a y , a z ) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x + 1 4 = y 2 = z — 3 — 5 . Запишите координаты всех направляющих векторов для нее.

Решение

Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a → = ( 4 , 2 , — 5 ) , а множество всех подобных векторов можно сформулировать как μ · a → = 4 · μ , 2 · μ , — 5 · μ . Здесь параметр μ – любое действительное число (за исключением нуля).

Ответ: 4 · μ , 2 · μ , — 5 · μ , μ ∈ R , μ ≠ 0

Запишите канонические уравнения, если прямая в пространстве проходит через M 1 ( 0 , — 3 , 2 ) и имеет направляющий вектор с координатами — 1 , 0 , 5 .

Решение

У нас есть данные, что x 1 = 0 , y 1 = — 3 , z 1 = 2 , a x = — 1 , a y = 0 , a z = 5 . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 0 — 1 = y — ( — 3 ) 0 = z — 2 5 ⇔ ⇔ x — 1 = y + 3 0 = z — 2 5

Ответ: x — 1 = y + 3 0 = z — 2 5

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров a x , a y , a z в уравнениях могут иметь нулевые значения. При этом запись x — x 1 a x = y — y 1 a y = z — z 1 a z = λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ ∈ R ):

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Рассмотрим эти случаи подробнее. Допустим, что a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , либо a x ≠ 0 , a y ≠ 0 , a z = 0 . В таком случае нужные уравнения мы можем записать так:

В первом случае:
x — x 1 0 = y — y 1 a y = z — z 1 a z = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x — x 1 = 0 y — y 1 a y = z — z 1 a z = λ

Во втором случае:
x — x 1 a x = y — y 1 0 = z — z 1 a z = λ ⇔ x = x 1 + a x · λ y — y 1 = 0 z = z 1 + a z · λ ⇔ y — y 1 = 0 x — x 1 a x = z — z 1 a z = λ

В третьем случае:
x — x 1 a x = y — y 1 a y = z — z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z — z 1 = 0 ⇔ z — z 1 = 0 x — x 1 a x = y — y 1 a y = λ

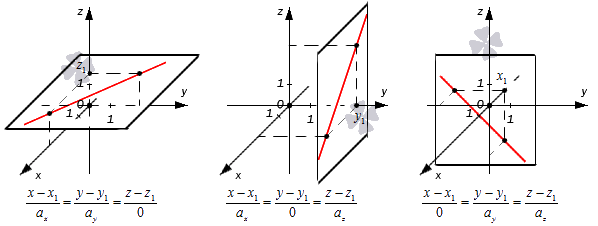
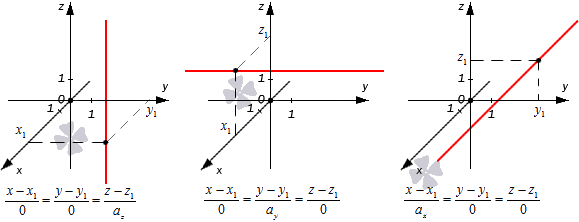
Получается, что при таком значении параметров нужные прямые находятся в плоскостях x — x 1 = 0 , y — y 1 = 0 или z — z 1 = 0 , которые располагаются параллельно координатным плоскостям (если x 1 = 0 , y 1 = 0 либо z 1 = 0 ). Примеры таких прямых показаны на иллюстрации.

Следовательно, мы сможем записать канонические уравнения немного иначе.

1. В первом случае: x — x 1 0 = y — y 1 0 = z — z 1 a z = λ ⇔ x — x 1 = 0 y — y 1 = 0 z = z 1 + a z · λ , λ ∈ R
2. Во втором: x — x 1 0 = y — y 1 a y = z — z 1 0 = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ , λ ∈ R z — z 1 = 0
3. В третьем: x — x 1 a x = y — y 1 0 = z — z 1 0 = λ ⇔ x = x 1 + a x · λ , λ ∈ R y = y 1 = 0 z — z 1 = 0

Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x 1 = 0 y 1 = 0 , x 1 = 0 z 1 = 0 , y 1 = 0 z 1 = 0 . Их направляющие векторы имеют координаты 0 , 0 , a z , 0 , a y , 0 , a x , 0 , 0 . Если обозначить направляющие векторы координатных прямых как i → , j → , k → , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

Покажем на примерах, как применяются эти правила.

Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые O z , O x , O y .

Решение

Координатные векторы i → = ( 1 , 0 , 0 ) , j → = 0 , 1 , 0 , k → = ( 0 , 0 , 1 ) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O ( 0 , 0 , 0 ) , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.

Для прямой O x : x 1 = y 0 = z 0

Для прямой O y : x 0 = y 1 = z 0

Для прямой O z : x 0 = y 0 = z 1

Ответ: x 1 = y 0 = z 0 , x 0 = y 1 = z 0 , x 0 = y 0 = z 1 .

В пространстве задана прямая, которая проходит через точку M 1 ( 3 , — 1 , 12 ) . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.

Решение

Учитывая условие параллельности, мы можем сказать, что вектор j → = 0 , 1 , 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:

x — 3 0 = y — ( — 1 ) 1 = z — 12 0 ⇔ x — 3 0 = y + 1 1 = z — 12 0

Ответ: x — 3 0 = y + 1 1 = z — 12 0

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

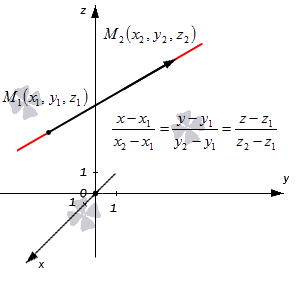
Допустим, что у нас есть две несовпадающие точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор M 1 M 2 → (или M 2 M 1 → ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

M 1 M 2 → = x 2 — x 1 , y 2 — y 1 , z 2 — z 1

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1

Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Приведем пример решения задачи.

в пространстве есть две точки с координатами M 1 ( — 2 , 4 , 1 ) и M 2 ( — 3 , 2 , — 5 ) , через которые проходит прямая. Запишите канонические уравнения для нее.

Решение

Согласно условиям, x 1 = — 2 , y 1 = — 4 , z 1 = 1 , x 2 = — 3 , y 2 = 2 , z 2 = — 5 . Нам требуется подставить эти значения в каноническое уравнение:

x — ( — 2 ) — 3 — ( — 2 ) = y — ( — 4 ) 2 — ( — 4 ) = z — 1 — 5 — 1 ⇔ x + 2 — 1 = y + 4 6 = z — 1 — 6

Если мы возьмем уравнения вида x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , то у нас получится: x — ( — 3 ) — 3 — ( — 2 ) = y — 2 2 — ( — 4 ) = z — ( — 5 ) — 5 — 1 ⇔ x + 3 — 1 = y — 2 6 = z + 5 — 6

Ответ: x + 3 — 1 = y — 2 6 = z + 5 — 6 либо x + 3 — 1 = y — 2 6 = z + 5 — 6 .

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида x — x 1 a x = y — y 1 a y = z — z 1 a z не очень удобно. Для решения некоторых задач лучше использовать запись x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ z — z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Значение параметра λ может быть любым действительным числом, ведь и x , y , z могут принимать любые действительные значения.

В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x — 2 3 = y — 2 = z + 7 0 . Запишите каноническое уравнение в параметрическом виде.

Решение

Сначала приравниваем каждую часть дроби к λ .

x — 2 3 = y — 2 = z + 7 0 ⇔ x — 2 3 = λ y — 2 = λ z + 7 0 = λ

Теперь разрешаем первую часть относительно x , вторую – относительно y , третью – относительно z . У нас получится:

x — 2 3 = λ y — 2 = λ z + 7 0 = λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7 + 0 · λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7

Ответ: x = 2 + 3 · λ y = — 2 · λ z = — 7

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство x — x 1 a x = y — y 1 a y = z — z 1 a z нужно для начала представить в виде системы уравнений:

x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a x y — y 1 a y = z — z 1 a z

Поскольку p q = r s мы понимаем как p · s = q · r , то можно записать:

x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a z y — y 1 a y = z — z 1 a z ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) a z · ( x — x 1 ) = a x · ( z — z 1 ) a z · ( y — y 1 ) = a y · ( z — z 1 ) ⇔ ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0

В итоге у нас вышло, что:

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0

Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2 , поскольку a y — a x 0 a z 0 — a x 0 a z — a y = 0 и один из определителей второго порядка не равен 0 :

a y — a x a z 0 = a x · a z , a y 0 a z — a x = a x · a y , — a x 0 0 — a x = a x 2 a y — a x 0 a z = a y · a z , a y 0 0 — a y = — a y 2 , — a x 0 a z — a y = a x · a y a z 0 0 a z = a z 2 , a z — a x 0 — a y = — a y · a z , 0 — a x a z — a y = a x · a z

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.

Прямая задана каноническим уравнением x — 1 2 = y 0 = z + 2 0 . Напишите для нее уравнение пересекающихся плоскостей.

Решение

Начнем с попарного приравнивания дробей.

x — 1 2 = y 0 = z + 2 0 ⇔ x — 1 2 = y 0 x — 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · ( x — 1 ) = 2 y 0 · ( x — 1 ) = 2 · ( z + 2 ) 0 · y = 0 · ( z + 2 ) ⇔ y = 0 z + 2 = 0 0 = 0

Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x , y и z . В таком случае x — 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0 .

Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x — 1 2 = y 0 = z + 2 0

Ответ: y = 0 z + 2 = 0

Прямая задана уравнениями x + 1 2 = y — 2 1 = z — 5 — 3 , найдите уравнение двух плоскостей, пересекающихся по данной прямой.

Решение

Приравниваем дроби попарно.

x + 1 2 = y — 2 1 = z — 5 — 3 ⇔ x + 1 2 = y — 2 1 x + 1 2 = z — 5 — 3 y — 2 1 = z — 5 — 3 ⇔ ⇔ 1 · ( x + 1 ) = 2 · ( y — 2 ) — 3 · ( x + 1 ) = 2 · ( z — 5 ) — 3 · ( y — 2 ) = 1 · ( z — 5 ) ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + 7 — 11 = 0

Получаем, что определитель основной матрицы полученной системы будет равен 0 :

1 — 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + ( — 2 ) · 2 · 0 + 0 · 3 · 3 — 0 · 0 · 0 — 1 · 2 · 3 — ( — 2 ) · 3 · 1 = 0

Минор второго порядка нулевым при этом не будет: 1 — 2 3 0 = 1 · 0 — ( — 2 ) · 3 = 6 . Тогда мы можем принять его в качестве базисного минора.

В итоге мы можем вычислить ранг основной матрицы системы x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 . Это будет 2. Третье уравнение исключаем из расчета и получаем:

x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0

Ответ: x — 2 y + 5 = 0 3 x + 2 z — 7 = 0

Задача 61746 Составить каноническое уравнение.

Условие

Составить каноническое уравнение параболы, если известно, что: а) парабола имеет фокус F (0, 2) и вершину в точке О (0, 0); б) парабола симметрична относительно оси абсцисс и проходит через точки О (0, 0) и М( 1, —4); в) парабола симметрична относительно оси ординат Оу и проходит через точки 0 (0, 0) и N(6, —2).

Решение

а) парабола имеет фокус F (0, 2) и вершину в точке О

О т в е т. x^2=2*4y

б) парабола симметрична относительно оси абсцисс и проходит через точку О (0, 0)

значит уравнение принимает вид:

парабола проходит через точy
М( 1, —4)

подставляем координаты точки в уравнение:

О т в е т. y^2=2*8x

в) парабола симметрична относительно оси ординат Оу и проходит через точку 0 (0, 0)

значит уравнение принимает вид:

парабола проходит через точy
N(6, —2).

Написать каноническое уравнение симметричного относительно

Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, равная 2 a .

Обозначим фокусы через F ₁ и F ₂ , расстояние между ними через 2 c , а сумму расстояний от произвольной точки эллипса до фокусов – через 2 a . По определению 2 a > 2 c , то есть a > c .

Выберем систему координат так, чтобы фокусы F ₁ и F ₂ лежали на оси 0 x , а начало координат совпадало с серединой отрезка F ₁ F ₂ . Тогда фокусы имют координаты: F ₁ (– c ;0) и F ₂ ( c ;0) . Пусть M ( x ; y ) – произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать

По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:

Это уравнение равносильно первоначальному. Оно называется каноническим уравнением эллипса – кривой второго порядка .

Установим форму эллипса, пользуясь его каноническим уравнением.

1. Уравнение (2.17) содержит x и y только в четных степенях, поэтому если точка ( x ; y ) принадлежит эллипсу, то ему также принадлежат точки (– x ; y ), ( x ;– y ), (– x ;– y ) . Отсюда: эллипс симметричен относительно осей 0 x и 0 y , а также относительно точки O (0;0), которую называют центром эллипса.

2. Найдем точки пересечения эллипса с осями координат. Положив y = 0, найдем точки A ₁ ( a ; 0) и A ₂ (– a ; 0), в которых ось 0 x пересекает эллипс. Положив в уравнении (2.17) x = 0, находим точки пересечения эллипса с осью 0 y : B ₁ (0; b ) и B ₂ (0;– b ). Точки A ₁ , A ₂ , B ₁ , B ₂ называются вершинами эллипса. Отрезки А₁А₂, В₁В₂, а также их длины 2 a и 2 b – соответственно большая и малая оси эллипса (рис. 2.4).

3. Из уравнения (2.17) следует, что каждое слагаемое в левой части не превосходит единицы, т.е.:

Следовательно, все точки эллипса лежат внутри прямоугольника, ограниченного прямыми x = ± a и y = ± b .

4. В уравнении (2.17) левая часть – сумма неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет уменьшаться, если | x | возрастает, | y | уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму овальной замкнутой кривой. Форма эллипса зависит от отношения . При a = b эллипс превращается в окружность, уравнение эллипса (2.17) принимает вид : x 2 + y 2 = a 2 . Отношение половины расстояния между фокусами к большой полуоси эллипса – эксцентриситет эллипса . Причем 0 ε 1, так как 0 c a .

Отсюда видно, что чем меньше эксцентриситет эллипса, тем будет менее эллипс сплющенным; при ε = 0 эллипс превращается в окружность.

Прямые – директрисы эллипса.

Если r – расстояние от произвольной точки до какого–нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение есть величина постоянная, равная эксцентриситету эллипса: .

Из равенства a 2 – c 2 = b 2 следует, что a > b . Если же наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2 b лежит на оси 0 y , а малая ось 2 a – на оси 0 x . Фокусы такого эллипса находятся в точках F ₁ (0; c ) и F ₂ (0;– c ) , где . Данный эллипс будет растянут вдоль оси 0 y .

Пример 2.5. Составить уравнение линии, для каждой точки которой отношение расстояний от нее до точки A (3;0) и до прямой x = 12, равно числу ε =0,5 . Полученное уравнение привести к простейшему виду .

Решение . Пусть M ( x ; y ) – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр MB на прямую . Тогда точка B( 12;y) . По условию задачи .

По формуле расстояния между двумя точками получаем:

Эксцентриситет эллипса

Примечание. Если эллипс (окружность) вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)

Пример 2.6. В геодезии используется система географических координат, основанная на понятии геоида. Геоид – поверхность Земли, ограниченная уровенной поверхностью, продолженной под континенты. Поверхность геоида отличается от физической поверхности Земли, на которой резко выражены горы и океанические впадины.

Тело, поверхность которого более всего соответствует поверхности геоида, имеет определенные размеры и ориентирована соответственно в теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех геодезических работ принят референц–эллипсоид Красовского с параметрами a = 6 378 245 м, b = 6 356 863 м, α = 1: 298,3.

Линия, проходящая вертикально через центр эллипсоида является полярной осью. Линия, проходящая через центр эллипсоида, перпендикулярно к полярной оси, – экваториальной осью. При пересечении поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно к полярной оси, образуется окружность, называемая экватором. Окружность, полученная от пересечения поверхности эллипсоида плоскостью, параллельной плоскости экватора, называется параллелью. Линия пересечения поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную ось, называется меридианом данной точки. Положение точки на земной поверхности определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной линией называется географической широтой. Для определения долгот точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол λ, составленный плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана, называется географической долготой

Гипербола – геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости – фокусов, есть величина постоянная, равная 2 a .

Обозначим фокусы через F ₁ и F ₂ , расстояние между ними через 2 c , а модуль разности расстояний от каждой точки гиперболы до фокусов через 2 a . По определению 2 a 2 c , то есть a c .

Выберем систему координат x 0 y так, чтобы фокусы F ₁ и F ₂ лежали на оси 0 x , а начало координат совпало с серединой отрезка F ₁ F ₂ . Тогда фокусы будут иметь координаты F 1( c ;0 ) и F ₂ (– c ;0 ). На этой основе выведем уравнение гиперболы. Пусть M ( x ; y ) – ее произвольная точка . Тогда по определению | MF ₁ – MF ₂ |= 2 a , то есть . Проведя преобразования, аналогичные упрощениям уравнения эллипса, получим каноническое уравнение гиперболы:

где b 2 = a 2 – c 2 . Гипербола – линия 2–го порядка.

Установим форму гиперболы, исходя из ее канонического уравнения.

1. Уравнение (2.18) содержит x и y только в четных степенях. Следовательно, гипербола симметрична относительно осей координат 0 x и 0 y , и относительно точки O (0;0) – центра гиперболы.

2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (2.18) y =0 , находим две точки пересечения гиперболы с осью 0 x : A ₁ ( a ; 0) и A ₂ (– a ; 0).

Положив в (2.18) x = 0, получаем y 2 = – b 2 , чего быть не может. Т.е. гипербола ось 0 y не пересекает.

3. Из уравнения (2.18) следует, что уменьшаемое . Это означает, что точки гиперболы расположены справа от прямой x = a (правая ветвь гиперболы) и слева от прямой x =– a (левая ветвь) (рис. 2.6).

4. Из уравнения (2.18) гиперболы видно, что когда | x | возрастает, то | y | также возрастает . Это следует из того, что разность – сохраняет значение, равно e единице. Следовательно, гипербола имеет форму, состоящую из двух неограниченных ветвей.

Прямая L называется асимптотой некоторой неограниченной кривой , если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном удалении т очки M вдоль кривой от начала координат.

Покажем, что гипербола имеет две асимптоты: . Так как данные прямые и гипербола (2.18) симметричны относительно координатных осей, то достаточно рассмотреть только точки, расположенные в первой четверти.

Возьмем на прямой точку N , имеющую ту же абсциссу, что и точка M ( x ; y ) на гиперболе . Найдем разность | MN | :

Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка | MN | стремится к нулю. Так как | MN | больше расстояния d от точки M до прямой L, то d стремится к нулю тем более ( и подавно) . Следовательно, прямые – есть асимптоты гиперболы (рис. 2.7).

Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы .

Эксцентриситет гиперболы – отношение расстояния между фокусами к величине её действительной оси, обозначается ε : . Так как у гиперболы c > a , то эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как . Видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение ее полуосей, а значит, тем более вытянут ее основной прямоугольник.

Эксцентриситет равносторонней гиперболы равен . Действительно, . Фокальные радиусы , для точек правой ветви гиперболы имеют вид: r ₁ = εx + a , r ₂ = εx – a ; для точек левой ветви: r ₁ =–( εx + a ), r ₂ =–( εx – a ) .

Прямые называются директрисами гиперболы. Тот факт, что для гиперболы ε > 1, то означает : правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной. Директрисы гиперболы имеют тоже свойство , что и директрисы эллипса.

Уравнение определяет гиперболу с действительной осью 2 b , расположенной на оси 0 y , и мнимой осью 2 a, расположенной на оси абсцисс (подобная гипербола изображена на рисунке 2.7 пунктиром).

Значит , гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Примечание. Если у кривой 2–го порядка смещен центр в некоторую точку O ’ ( x ₀ ; y ₀ ) , то она называется нецентральной кривой. Уравнение такой кривой имеет вид:

Примечание. При вращении гиперболы вокруг ее действительной оси образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид

Подробно данные уравнения рассмотрены в теме: «Исследование общего уравнения 2–ой степени» (смотри схему 10), частными случаями которого являются данные формулы.