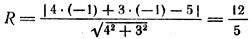Написать уравнение диаметра окружности перпендикулярного прямой

Задача 11414 Найти уравнение прямой, содержащей.

Условие

Найти уравнение прямой, содержащей диаметр окружности
х^2 + у^2 — 6х + 4у + 8 = 0, перпендикулярный прямой х — Зу + 2 = 0.

Решение

Найдем центр и радиус окружности
х^2 + у^2 — 6х + 4у + 8 = 0,
для этого выделяем полные квадраты
х^2 -6х + 9 + у^2 + 4у + 4 — 9 — 4 + 8 = 0,
(х-3)^2+(y+2)^2=5
Центр окружности в точке (3;-2)

Нормальные векторы взаимно перпендикулярных прямых перпендикулярны, значит их скалярное произведение равно 0.
Нормальный вектор прямой Ах+Ву+С=0 имеет координаты
(А;В)
Нормальный вектор прямой х-3у+2=0 имеет координаты
(1;-3).
Пусть прямая Ах+Ву+С=0 перпендикулярна данной.
Тогда скалярное произведение векторов (1;-3) и (А;В) равно 0
1*А+(-3)*В=0
Можно взять, например,
А=3 В=1
Уравнение прямой перпендикулярной х — Зу + 2 = 0 имеет вид
3х+у+С=0
Чтобы найти С подставим координаты точки О(3;-2) в это уравнение
3*3+1*(-2)+С=0
С=-7
О т в е т. 3x+y-7=0

Написать уравнение диаметра окружности перпендикулярного прямой

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

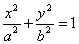
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

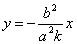
Если гипербола задана уравнением

, (2)

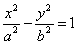
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

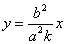
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

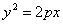
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

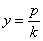
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

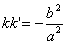
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

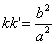
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Найти уравнение диаметра окружности перпендикулярного прямой

Найти уравнение диаметра окружности перпендикулярного прямой

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

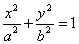
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

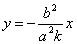
Если гипербола задана уравнением

, (2)

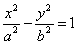
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

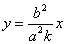
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

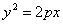
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

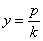
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

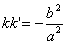
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

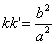
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Задача 11414 Найти уравнение прямой, содержащей.

Условие

Найти уравнение прямой, содержащей диаметр окружности
х^2 + у^2 — 6х + 4у + 8 = 0, перпендикулярный прямой х — Зу + 2 = 0.

Решение

Найдем центр и радиус окружности
х^2 + у^2 — 6х + 4у + 8 = 0,
для этого выделяем полные квадраты
х^2 -6х + 9 + у^2 + 4у + 4 — 9 — 4 + 8 = 0,
(х-3)^2+(y+2)^2=5
Центр окружности в точке (3;-2)

Нормальные векторы взаимно перпендикулярных прямых перпендикулярны, значит их скалярное произведение равно 0.
Нормальный вектор прямой Ах+Ву+С=0 имеет координаты
(А;В)
Нормальный вектор прямой х-3у+2=0 имеет координаты
(1;-3).
Пусть прямая Ах+Ву+С=0 перпендикулярна данной.
Тогда скалярное произведение векторов (1;-3) и (А;В) равно 0
1*А+(-3)*В=0
Можно взять, например,
А=3 В=1
Уравнение прямой перпендикулярной х — Зу + 2 = 0 имеет вид
3х+у+С=0
Чтобы найти С подставим координаты точки О(3;-2) в это уравнение
3*3+1*(-2)+С=0
С=-7
О т в е т. 3x+y-7=0

Составить уравнение диаметра окружности параллельно прямой

Составить уравнение диаметра окружности параллельно прямой

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

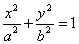
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

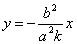
Если гипербола задана уравнением

, (2)

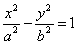
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

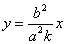
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

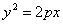
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

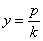
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

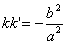
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

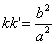
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Задача 11414 Найти уравнение прямой, содержащей.

Условие

Найти уравнение прямой, содержащей диаметр окружности
х^2 + у^2 — 6х + 4у + 8 = 0, перпендикулярный прямой х — Зу + 2 = 0.

Решение

Найдем центр и радиус окружности
х^2 + у^2 — 6х + 4у + 8 = 0,
для этого выделяем полные квадраты
х^2 -6х + 9 + у^2 + 4у + 4 — 9 — 4 + 8 = 0,
(х-3)^2+(y+2)^2=5
Центр окружности в точке (3;-2)

Нормальные векторы взаимно перпендикулярных прямых перпендикулярны, значит их скалярное произведение равно 0.
Нормальный вектор прямой Ах+Ву+С=0 имеет координаты
(А;В)
Нормальный вектор прямой х-3у+2=0 имеет координаты
(1;-3).
Пусть прямая Ах+Ву+С=0 перпендикулярна данной.
Тогда скалярное произведение векторов (1;-3) и (А;В) равно 0
1*А+(-3)*В=0
Можно взять, например,
А=3 В=1
Уравнение прямой перпендикулярной х — Зу + 2 = 0 имеет вид
3х+у+С=0
Чтобы найти С подставим координаты точки О(3;-2) в это уравнение
3*3+1*(-2)+С=0
С=-7
О т в е т. 3x+y-7=0

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

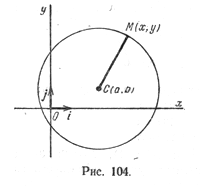
Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = \( \sqrt \), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

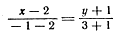
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

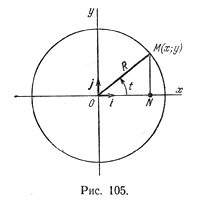
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем