Написать уравнение энергии магнитного поля

Написать уравнение энергии магнитного поля

Электромагнитные колебания и волны

Для колебательного контура предыдущей задачи написать уравнение (с числовыми коэффициентами) изменения со временем t энергии электрического поля W_эл, энергии магнитного поля W_м и полной энергии поля W. Найти энергию электрического поля, энергию магнитного поля и полную энергию поля в моменты времени Т/8, Т/4 и Т/2. Построить графики этих зависимостей в пределах одного периода.

Дано:

q = 2,5 мкКл = 2,5·10 -6 Кл

Решение:

Энергия электрического поля на обкладках конденсатора

Энергия магнитного поля в катушке индуктивности

Полная энергия в контуре

Закон изменения напряжения на обкладках конденсатора

Период колебаний находим по формуле Томсона

Циклическая частота связана с периодом соотношением

Уравнение колебания напряжения запишется в виде

Аналогично можно записать уравнение изменения заряда на обкладках конденсатора

Ток в контуре – первая производная от заряда по времени

Лекция 14. Энергия магнитного поля. Уравнения Максвелла в веществе

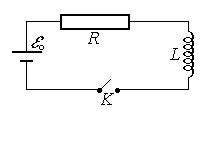Рассмотрим цепь, содержащую активное сопротивление R, катушку индуктивности L и источник эдс e_o (рис.49). При замыкании ключа К ток начнет возрастать, вследствие этого появится эдс самоиндукции e_s. По закону Ома, RI=e_o+e_s, следовательно,

Умножая обе части на Idt, получим

где левая часть представляет собой работу сторонних сил dА*, первое слагаемое справа — джоулево тепло. Последнее слагаемое равно IdФ (так как e_S=-dФ/dt). Таким образом,

следовательно, dА*>dQ, а часть работы (IdФ=ILdI) совершается против эдс самоиндукции. За счет этой работы контур накапливает энергию, которую вычислим, интегрируя последнее выражение

W = 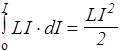. (150)

Выразим энергию магнитного поля через В. Действительно, L=mm_on 2 V, как индуктивность длинного соленоида, поэтому

W = .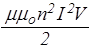

Но так как для соленоида В=mm_onI, и B=mm_oH, следовательно,

,

где слева стоит энергия поля в единице объема, т.е. плотность энергии. Расчет показывает, что это верно и в векторном виде

, (151)

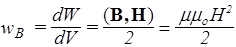
где w_B — плотность энергии магнитного поля, которая для неоднородного поля равна производной: w_B=dW/dV.

Уравнения Максвелла для среды в интегральной форме. Выпишем уравнения Максвелла для среды в интегральной форме в виде таб.2, где в правой колонке дадим их формулировки.

Уравнения Максвелла для среды в интегральной форме. Таблица 2

I		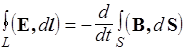Циркуляция вектора Е по любому замкнутому контуру равна минус производной по времени от магнитного потока через любую поверхность, ограниченную этим контуром. Под Е понимается как вихревое, так и электростатическое поле
II		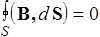Поток вектора В сквозь любую замкнутую поверхность равен нулю
III		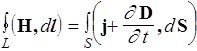Циркуляция вектора Н по любому замкнутому контуру равна полному току (проводимости и смещения) через любую поверхность, ограниченную данным контуром
IV		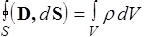Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью

По форме уравнения Максвелла для вещества и вакуума идентичны. Однако для описания электрического и магнитного полей в вакууме введение векторов D и Н не являлось принципиально необходимым. Рассуждения, с помощью которых мы пришли к уравнениям Максвелла, не могут претендовать на роль доказательств. Эти уравнения в общем случае нельзя «вывести» — они являются основными аксиомами электродинамики.

Уравнения Максвелла в веществе в дифференциальной форме. В принципе эти уравнения уже были нами сформулированы. Выпишем их еще раз, используя параллельно оператор набла

I. , .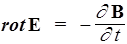

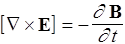
II. div B= 0, .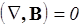

III. , ,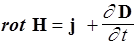

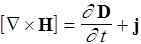
IV. div D =r, (Ñ,D) = r.

В этой форме уравнения утверждают следующее. Электрическое поле может возникнуть по двум причинам. Во-первых, его источниками являются электрические заряды (и сторонние, и связанные — это следует из последнего уравнения, где D=e_оЕ+Р и (Ñ,P)=-r’, следовательно, (Ñ,E)

r+r’); во-вторых,- переменное магнитное поле. Как видно из уравнения III, магнитное поле может порождаться движущимися зарядами и переменными электрическими полями: так как Н=m₀B—J и [Ñ´J]=j‘, следовательно, [Ñ´B]

j+j’+¶Р/¶t+e_о¶E/¶t. Первые три тока связаны с движением зарядов, последний — с изменяющимся во времени электрическим полем Е. Источников магнитных зарядов не существует (это показывает уравнение II).

Материальные уравнения. Фундаментальные уравнения Максвелла не составляют полной системы уравнений: их недостаточно для нахождения полей по заданным распределениям зарядов и токов. Для этого их необходимо дополнить соотношениями, характеризующими свойства среды. Эти соотношения называются материальными уравнениями.

Материальные уравнения просты (и нам уже знакомы) в случае достаточно слабых электромагнитных полей, медленно меняющихся в пространстве и во времени. Для изотропных сред, несодержащих сегнетоэлектриков и ферромагнетиков, материальные уравнения имеют вид

D= ee_oE, B= mm_oH, j= s(E+ E*).

Величины e, m и s характеризуют электрические и магнитные свойства среды; E* — напряженность поля сторонних сил.

Энергия магнитного поля в веществе

Допустим, что у нас есть магнитное поле, созданное фиксированным распределением токов в пространстве. Его индукцию можно вычислить так:

B 0 → ( x , y , z ) = μ o H 0 → ( x , y , z ) .

А энергию этого магнитного поля – так:

W m = B 2 / 2 μ μ 0 .

Теперь представим, что все пространство заполнено однородным магнетиком с магнитной проницаемостью, равной μ = c o n s t . Примем, что поле создается тем же распределением токов. Тогда его напряженность не будет меняться:

А индукцию данного поля можно вычислить по формуле:

B = F L q υ sin a .

Тогда из двух предыдущих уравнений мы можем найти энергию магнитного поля при наличии магнетика:

w m = 1 2 H → B → = 1 2 B 2 μ μ 0 .

Из данного выражения можно сделать вывод, что энергия магнитного поля растет по мере заполнения пространства однородным магнетиком. Это объясняется сторонними движущими силами, придающими энергию процессу, т.к. они поддерживают токи постоянными. Поскольку источники энергии остаются прежними и после заполнения пространства магнетиком, то можно предположить, что энергия магнетика во внешнем поле будет равна:

W B = 1 2 ∫ V 1 μ 0 — 1 μ B · B i d v .

Теперь вспомним о таких понятиях, как векторы напряженности и векторы намагниченности. Они связаны между собой выражением:

Здесь буквой x обозначается магнитная восприимчивость, которая в случае с изотропными магнетиками соотносится с магнитной проницаемостью следующим образом:

Преобразуем подынтегральное выражение и используем формулы, выведенные до этого. Получим:

Тогда энергия магнетика будет равна:

Полученная формула будет иметь ту же структуру, что и формула вычисления энергии диэлектрика во внешнем электрическом поле, но с другим знаком справа. Она рассчитана изначально для магнетика, имеющего постоянную магнитную проницаемость, однако в других случаях ее также можно использовать.

Как изменяется энергия магнетика при изменении магнитной проницаемости среды

Возьмем среду с магнитной проницаемостью μ 2 , в которой находится магнетик с проницаемостью μ 1 . Тогда в соответствии с выведенной ранее формулой запишем, что:

Здесь H 2 → — это напряженность поля в точках магнетика с проницаемостью μ 2 (предположим, что другого магнетика у нас нет), H 1 → – фактическая напряженность поля в магнетике с проницаемостью
μ 1 .

Если магнитная проницаемость среды изменяется на бесконечно малую величину δ μ = μ 1 — μ 2 , то энергия магнетика во внешнем магнитном поле напряженностью H → изменяется на δ W m υ .

Подставим в формулу H 2 → = H → , H 1 → = H → + δ H → , откинем величину δ μ δ H → · H → и получим:

Решение задач на нахождение энергии магнитного поля

Условие: у нас есть соленоид с током без сердечника. Плотность энергии создаваемого им магнитного поля равна 0 , 1 Д ж м 3 . Найдите увеличение плотности энергии при включении в соленоид железного сердечника. Сила тока при этом останется прежней.

Решение

Сразу отметим, что магнитная проницаемость среды для соленоида без сердечника будет равна единице. Чтобы найти напряженность магнитного поля соленоида, используем следующую формулу:

Выразим напряженность из формулы и получим:

При включении в соленоид сердечника напряженность поля останется прежней, а для вычисления индукции возьмем эту формулу:

H = 2 · 0 , 1 4 π · 10 — 7 = 0 , 4 · 10 3 .

Для нахождения индукции по напряженности магнитного поля в железном сердечнике нам нужно будет заглянуть в справочник. Он может быть представлен как в табличной, так и графической форме. Найдем там нужную величину, равную B ≈ 1 Т л . Теперь перейдем к вычислению плотности магнитной энергии поля соленоида с железным сердечником:

Теперь вычисляем значение w ‘ :

w ‘ = 1 · 400 2 = 200 .

После чего найдем искомое соотношение плотностей:

w ‘ w = 200 0 , 1 = 2000 .

Ответ: при включении железного сердечника плотность энергии возрастет в 2 тысячи раз.

Условие: у нас есть квадратная железная рамка с обмоткой из n -ного количества витков, по которой течет ток с силой I . В ней есть прорезь шириной a . Вычислите величину энергии магнитного поля в зазоре рамки, если длина ее средней линии равна d , а площадь поперечного сечения – S . Магнитную проницаемость рамки взять равной μ , рассеяние поля в краях прорези не учитывать.

Решение

Начнем с вычисления напряженности магнитного поля в самой рамке и ее зазоре. Для этого нам понадобится теорема о циркуляции:

∮ L H → d l → = ∑ k = 1 N I k .

Согласно условиям нашей задачи, основная формула будет иметь следующий вид:

H ( d — a ) + H a = I N → H = I N d .

Теперь найдем величину магнитной индукции в зазоре:

Подставим нужные значения и вычислим:

H ( d — a ) + B μ 0 a = I N → B = μ 0 I N a — μ 0 ( d — a ) H a .

Энергия магнитного поля в зазоре будет равна:

W m 1 = B H 2 S · a = 1 2 μ 0 I N a — μ 0 ( d — a ) I N d a I N d · S · a = 1 2 μ 0 a ( I N ) 2 S d .

Теперь вычислим магнитную энергию в сердечнике:

W m 2 = μ μ 0 H 2 2 S ( d — a ) = μ μ 0 H 2 2 I N d 2 ( d — a ) .

Нам осталось только найти полную энергию поля:

W m = W m 1 + W m 2 = 1 2 μ 0 a ( I N ) 2 S d + μ μ 0 H 2 2 I N d 2 ( d — a ) = 1 2 μ 0 S ( I N ) 2 d a + μ d ( d — a ) .

Ответ: W m 1 = 1 2 μ 0 a ( I N ) 2 S d , W m = 1 2 μ 0 S ( I N ) 2 d a + μ d ( d — a ) .