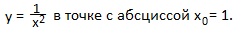Написать уравнение общей касательной к графикам двух функций

Написать уравнение общей касательной к графикам двух функций

Пусть функция определена в некоторой окрестности токи , непрерывна в этой точке и , а (рис.2).

Придав произвольное приращение аргументу , так чтобы , перейдем к точке с абсциссой и ординатой , где .

Уравнение прямой, проходящей через точки и (секущей графика функции , имеет вид: , где отношение представляет собой угловой коэффициент секущей ( .

Касательной к графику функции в точке называется предельное положение секущей , при стремлении точки по графику к точке .

Для того, чтобы секущая при стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел , то есть , чтобы существовала конечная производная функции в точке .

Угловой коэффициент касательной получается путем перехода от к пределу при :

Таким образом, получим, что , где — угол наклона касательной к оси (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной . Уравнение касательной к графику функции в точке имеет вид

В случае бесконечной производной .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при , получаем уравнение касательной к графику функции в точке в виде , то есть касательная является в данном случае вертикальной прямой, проходящей через точку оси абсцисс.

Пусть материальная точка движется прямолинейно и — длина пути, проходимого за время , отсчитываемого от некоторого момента времени .

Для определения скорости в данный момент придадим переменной некоторое приращение , при этом приращение пути будет равно .

Отношение называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени , и обозначается

Предел называется величиной мгновенной скорости движения в момент времени .

Таким образом, мгновенная скорость в момент времени прямолинейного движения, совершаемого по закону равна значению производной .

Задача 1. Составьте уравнение общей касательной к графикам функций и .

Прямая является общей касательной графиков функций и , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.

Прямые совпадают, если их угловые коэффициенты и свободные члены равны. Отсюда

Решением системы будут

Уравнения общих касательных имеют вид:

Уравнение касательной к кривой в точке с абсциссой имеет вид:

Для касания прямой параболы достаточно, чтобы дискриминант квадратного уравнения был равен нулю.

Ответ: Уравнения общих касательных имеют вид: и .

Задача 2. График функции пересекает ось абсцисс в точке , а касательная к графику пересекает ось абсцисс в точке . Напишите уравнение этой касательной, если точка делит пополам отрезок , где — начало координат.

Найдем абсциссу точки , решив уравнение .

Точка имеет координаты . — середина отрезка , значит, точка имеет координаты .

Функция определена при и дифференцируема при .

Составим уравнение касательной в точке графика с абсциссой .

Касательная проходит через точку . Значит,

Решим это уравнение.

Уравнение касательной имеет вид:

Задача 3. Точка движется прямолинейно под действием постоянной силы с ускорением 2 м / с и с нулевой начальной скоростью. Через три секунды после начала движения сила прекращает действовать, и точка начинает двигаться равномерно с набранной скоростью. Найдите закон движения точки.

Решение. Выберем систему координат так, чтобы в начальный момент времени точка находилась в начале координат, то есть при .

Закон движения при имеет вид: при . При графиком движения является прямая — касательная к параболе , проведенная в точке . Найдем уравнение этой касательной.

Таким образом, закон движения имеет вид:

Задача 4. Паром подтягивается к берегу при помощи каната, который наматывается на ворот со скоростью 40 м / мин. Ворот находится на берегу на 10 м выше поверхности воды. Найдите:

а) скорость движения парома в тот момент, когда он находится в 30 м от берега;

b) скорость движения парома в тот момент, когда длина натянутого каната равна 50 м.

а) Пусть м — расстояние от парома до берега. В выбранной системе координат в точке находится ворот, паром — в точке (рис. 3).

По теореме Пифагора:

При наматывании каната на ворот расстояние

С другой стороны,

Из решения уравнения находим искомую скорость движения: (м / мин). Знак «минус» означает, что паром приближается к берегу.

1. Составьте уравнение всех касательных к графику функции , которая проходит через точку :

Сколько существует решений в зависимости от выбора точки?

2. На графике функции найдите все точки, касательная в каждой из которых к этому графику отсекает от отрицательной полуоси ОХ отрезок вдвое меньше, чем от положительной полуоси ОУ.

3. На графике функции найти все такие точки, касательная в каждой из которых к графику пересекает положительные полуоси и отсекает от них равные по длине отрезки.

4. Доказать, что касательная к гиперболе образует с осями координат треугольник постоянной площади, а точка касания является центром окружности, описанной около этого треугольника.

5. График функции пересекает ось абсцисс в точке К, а касательная к графику пересекает ось абсцисс в точке С. Напишите уравнение этой касательной, если начало координат является серединой отрезка КС.

6. Напишите уравнение касательной к графику функции , не пересекающей прямой .

7. Прямая является касательной к графику функции . Найдите координаты точки касания.

8. Докажите, что касательная к графику функции в точке с абсциссой и наклонная асимптота графика функции параллельны.

9. Окружность радиуса 1 с центром на положительной полуоси ОУ касается параболы . Найти точку касания и положение центра окружности.

10. Составьте уравнение общей касательной к графикам функций:

11. Найдите все значения , при каждом из которых касательные к графикам функций и в точках с абсциссой параллельны.

12. На координатной плоскости построены две параболы и , и к ним проведены две общие касательные. Найдите уравнение этих общих касательных, а также координаты точек касания. Докажите, что четырехугольник с вершинами в точках касания является параллелограммом.

13. При каких значениях параметра , прямая, проходящая через точки и касается параболы ?

14. Найти величину угла, под которым парабола видна из точки .

15. Найти множество точек действительной оси над которыми касательная к графику функции образует с этой осью острый угол, параллельна оси, если

16. При каких значениях параметра , парабола, проходящая через точки и и касается прямой ?

17. Доказать, что при любом значении существует касательная к графику функции , перпендикулярная прямой .

18. Найти все значения параметра , при которых на графике функции существует единственная точка с отрицательной абсциссой, касательная в которой параллельна прямой .

19. Найти все такие числа и , что парабола касается прямых и .

20. При каких значениях существует ровно две точки на графике функции , касательные в которых к этому графику параллельны прямой

21. К параболе проведены две касательные. Одна из них касается левой ветви параболы и одновременно кривой, заданной уравнением . Тангенс угла между двумя касательными равен . Определите площадь фигуры, заключенной между параболой и этими касательными.

22. К графику функции в точке с абсциссой проведена касательная. Найдите расстояние от начала координат до этой касательной.

23. Для параболы точка является ее фокусом. Докажите, что лучи света, исходящие из фокуса, отражаются в любой точке параболы параллельно ее оси симметрии.

24. Дана функция . Докажите, что

фигуры, ограниченные отрезками горизонтальных касательных к графику функции и дугами этого графика между точками его пересечения с касательными имеют равные площади;

прямая, касающаяся графика функции в точке с абсциссой , где , пересечет этот график еще в одной точке, абсцисса которой .

25. Дана функция . Найдите

уравнения касательных к графику функции , параллельных прямой проходящей через точки с абсциссами 1 и 4 на этом графике;

множество значений углов наклона касательных к графику функции ;

уравнения тех касательных к графику данной функции , которые вместе с осями координат образуют треугольник, площадью .

26. К каждой ветви графика функции проведено по касательной. Пусть точки их пересечения с осями координат (рис. 4). Докажите, что треугольники AOD и BOC равновелики.

27. Две точки движутся по одной прямой по законам и . Каковы их скорости в момент встречи? В какой момент времени их скорости одинаковы? Постройте графики движения и поясните полученные результаты.

28. Покажите, что если точка движется по закону , то на нее действует постоянная сила. Будет ли сила постоянной, если ?

29. Высота тела, брошенного вертикально вверх, меняется в зависимости от времени по закону . Найдите скорость тела в конце десятой секунды. Сколько времени тело будет лететь вверх и какой наибольшей высоты оно достигнет.

30. Точка совершает прямолинейное колебательное движение по закону . Определите скорость и ускорение движения в момент времени . Покажите, что ускорение движения пропорционально отклонению .

31. Угол (в радианах), на который повернется колесо за секунд, равен . Найдите угловую скорость колеса в момент с и момент, когда колесо остановится.

32. При деформации одна из сторон прямоугольника увеличивается с постоянной скоростью 1 см / ч, а другая уменьшается со скоростью 0,5 см / ч. Найти скорость изменения площади прямоугольника через 45 минут после начала деформации, если известно, что в этот момент его площадь равна 20 см , а первоначальная площадь прямоугольника 17 см .

33. Человек приближается со скоростью м / с к подножию башни высотой м. Какова скорость его приближения к вершине башни, когда он находится на расстоянии м от основания?

34. Лестница, длиной 5 м, приставлена к стене таким образом, что верхний ее конец находится на высоте 4 м. В некоторый момент времени нижний конец лестницы начинает скользить по полу в направлении от стены, при этом верхний конец приближается к поверхности земли с постоянным ускорением 2 м /с . С какой скоростью удаляется от стены нижний конец лестницы в тот момент, когда верхний конец находится на высоте 2 м?

35. Из конусообразной воронки высыпается песок с постоянной скоростью а м / с. С какой скоростью будет понижаться уровень песка в воронке?

36. Лошадь бежит по окружности со скоростью 20 км / ч. В центре окружности стоит фонарь, по касательной к окружности в точке, откуда лошадь начинает свой бег, расположен забор. С какой скоростью будет перемещаться тень лошади вдоль забора в момент, когда лошадь пробежит окружности?

37. Человек приближающийся к вертикальной стене, освещен сзади фонарем, находящемся на расстоянии от стены. Скорость движения человека равна . С какой скоростью увеличивается его тень, если рост человека ?

Уравнение касательной к графику функции

п.1. Уравнение касательной

Рассмотрим кривую \(y=f(x)\).
Выберем на ней точку A с координатами \((x_0,y_0)\), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке \(x_0\): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: \((y_B-y_A)=k(x_B-x_A)\).
Для \(A(x_0,y_0),\ B(x,y)\) получаем: \begin (y-y_0)=k(x-x_0)\\ y=k(x-x_0)+y_0\\ y=f'(x_0)(x-x_0)+f(x_0) \end

Чтобы записать уравнение касательной с угловым коэффициентом в виде \(y=kx+b\), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=\underbrace_<=k>x+\underbrace_ <=b>$$

п.2. Алгоритм построения касательной

На входе: уравнение кривой \(y=f(x)\), абсцисса точки касания \(x_0\).
Шаг 1. Найти значение функции в точке касания \(f(x_0)\)
Шаг 2. Найти общее уравнение производной \(f’ (x)\)
Шаг 3. Найти значение производной в точке касания \(f'(x_0 )\)
Шаг 4. Записать уравнение касательной \(y=f’ (x_0)(x-x_0)+f(x_0)\), привести его к виду \(y=kx+b\)
На выходе: уравнение касательной в виде \(y=kx+b\)

Пусть \(f(x)=x^2+3\). Найдем касательную к этой параболе в точке \(x_0=1\).

\(f(x_0)=1^2+3=4 \)
\(f'(x)=2x \)
\(f'(x_0)=2\cdot 1=2\)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: \(y=2x+2\)

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода \(x_0\notin D\), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку \(x_0\in D\), входящую в область определения. График функции и касательная имеют одну общую точку \((x_0,y_0)\).

Вертикальные касательные характерны для радикалов вида \(y=\sqrt[n]\).

Пусть \(f(x)=\sqrt[5]+1\). Найдем касательную к этой кривой в точке \(x_0=1\).

\(f(x_0)=\sqrt[5]<1-1>+1=1\)
\(f'(x)=\frac15(x-1)^<\frac15-1>+0=\frac15(x-1)^<-\frac45>=\frac<1><5(x-1)^<\frac45>> \)
\(f'(x_0)=\frac<1><5(1-1)^<\frac45>>=\frac10=+\infty\)
В точке \(x_0\) проходит вертикальная касательная.
Её уравнение: \(x=1\)
Ответ: \(y=2x+2\)

п.4. Примеры

Пример 1. Для функции \(f(x)=2x^2+4x\)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0\Rightarrow 2x(x+2)=0\Rightarrow \left[ \begin x=0\\ x=-2 \end \right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке \(x_0=0\): \begin f(x_0)=0,\ \ f'(x)=4x+4\\ f'(x_0)=4\cdot 0+4=4\\ y=4(x-0)+0=4x \end Касательная в точке \(x_0=-2\): \begin f(x_0)=0,\ \ f'(x)=4x+4\\ f'(x_0)=4\cdot (-2)+4=-4\\ y=-4(x+2)+0=-4x-8 \end

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: \(f'(x)=4x+4\) По условию \(f'(x_0)=tg\alpha=tg45^\circ=1\) Решаем уравнение: $$ 4x_0+4=1\Rightarrow 4x_0=-3\Rightarrow x_0=-\frac34 $$ Точка касания \(x_0=-\frac34\) \begin f(x_0)=2\cdot\left(-\frac34\right)^2+4\cdot\left(-\frac34\right)=\frac98-3=-\frac<15> <8>\end Уравнение касательной: \begin y=1\cdot\left(x+\frac34\right)-\frac<15><8>=x-\frac98 \end

в) найдите, в какой точке касательная будет параллельна прямой \(2x+y-6=0\). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: \(y=-2x+6\Rightarrow k=-2\). Касательная должна быть параллельной, значит, её угловой коэффициент тоже \(k=-2\). Получаем уравнение: \begin f'(x_0)=-2\\ 4x_0+4=-2\Rightarrow 4x_0=-6\Rightarrow x_0=-\frac32 \end Точка касания \(x_0=-\frac32\) \begin f(x_0)=2\cdot\left(-\frac32\right)^2+4\cdot\left(-\frac32\right)=\\ =\frac92-6=-\frac32 \end Уравнение касательной: \begin y=-2\cdot\left(x+\frac32\right)-\frac32=-2x-\frac92 \end Или, в каноническом виде: \begin 2x+y+\frac92=0 \end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой \(k=0\). Получаем уравнение: \(f'(x_0)=0\). \begin 4x_0+4=0\Rightarrow 4x_0=-4\Rightarrow x_0=-1 \end Точка касания \(x_0=-1\) \begin f(x_0)=2\cdot(-1)^2+4\cdot(-1)=-2 \end Уравнение касательной: \begin y=0\cdot(x+1)-2=-2 \end

Ответ: а) \(y=4x\) и \(y=-4x-8\); б) \(y=x-\frac98\); в) \(2x+y+\frac92=0\); г) \(y=-2\)

Пример 3*. Найдите точку, в которой касательная к графику функции \(f(x)=\frac-x\) перпендикулярна прямой \(y=11x+3\). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой \(k_1=11\).
Угловой коэффициент перпендикулярной прямой \(k_2=-\frac<1>=-\frac<1><11>\) \begin f'(x)=\left(\frac\right)’-x’=\frac<2x(x+3)-(x^2+2)\cdot 1><(x+3)^2>-1=\frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\\ =\frac<(x+3)^2>=- \frac<11> <(x+3)^2>\end В точке касания: \begin f'(x_0)=k_2\Rightarrow=-\frac<11><(x+3)^2>=-\frac<1><11>\Rightarrow (x+3)^2=121\Rightarrow (x+3)^2-11^2=0\Rightarrow\\ \Rightarrow (x+14)(x+8)=0\Rightarrow \left[ \begin x=-14\\ x=8 \end \right. \end
Уравнение касательной при \(x_0=-14\) \begin f(x_0)=\frac<(-14)^2+2><-14+3>+14=\frac<198><-11>+14=-18+14=-4\\ y=-\frac<1><11>(x+14)-4=-\frac <11>\end Уравнение касательной при \(x_0=8\) \begin f(x_0)=\frac<8^2+2><8+3>-8=\frac<66><11>-8=-2\\ y=-\frac<1><11>(x-8)-2=-\frac <11>\end
Ответ: точка касания (-14;-4), уравнение \(y=-\frac<11>\)
и точка касания (8;-2), уравнение \(-\frac<11>\)

Пример 4*. Найдите уравнения общих касательных к параболам \(y=x^2-5x+6\) и \(y=x^2+x+1\). Укажите точки касания.

Найдем производные функций: \begin f_1′(x)=2x-5,\ \ f_2′(x)=2x+1 \end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных \(g_1(x)\) и \(g_2(x)\) через эти переменные. \begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\\ \\ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) \end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: \begin \begin 2a-5=2b+1\\ 6-a^2=1-b^2 \end \Rightarrow \begin 2(a-b)=6\\ a^2-b^2=5 \end \Rightarrow \begin a-b=3\\ (a-b)(a+b)=5 \end \Rightarrow \begin a-b=3\\ a+b=\frac53 \end \Rightarrow \\ \Rightarrow \begin 2a=3+\frac53\\ 2b=\frac53-3 \end \Rightarrow \begin a=\frac73\\ b=-\frac23 \end \end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2\cdot\frac73-5=-\frac13,\ \ b=6-a^2=6-\frac<49><9>=\frac59 $$ Уравнение общей касательной: $$ y=-\frac x3+\frac59 $$
Точки касания: \begin a=\frac73,\ \ f_1(a)=\left(\frac73\right)^2-5\cdot\frac73+6=\frac<49><9>-\frac<35><3>+6=\frac<49-105+54><9>=-\frac29\\ b=-\frac23,\ \ f_2(b)=\left(-\frac23\right)^2-\frac23+1=\frac49-\frac23+1\frac<4-6+9><9>=\frac79 \end
Ответ: касательная \(y=-\frac x3+\frac59\); точки касания \(\left(\frac73;-\frac29\right)\) и \(\left(-\frac23;\frac79\right)\)

Пример 5*. Докажите, что кривая \(y=x^4+3x^2+2x\) не пересекается с прямой \(y=2x-1\), и найдите расстояние между их ближайшими точками.

Решим уравнение: \(x^4+3x^2+2x=2x-1\) \begin x^4+3x^2+1=0\Rightarrow D=3^2-4=5\Rightarrow x^2=\frac<-3\pm\sqrt<5>> <2>\end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, \(x\in\varnothing\) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом \(k=2\), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой \(y=2x-1\).
Строим уравнение касательной. По условию: \(f'(x)=4x^3+6x+2=2\) \begin 4x^3+6x=0\Rightarrow 2x(2x^2+3)=0\Rightarrow \left[ \begin x=0\\ 2x^2+3=0 \end \right. \Rightarrow \left[ \begin x=0\\ x^2=-\frac32 \end \right. \Rightarrow \left[ \begin x=0\\ x\in\varnothing \end \right. \Rightarrow x=0 \end Точка касания \(x_0=0,\ y_0=0^4+3\cdot 0^2+2\cdot 0=0\).
Уравнение касательной: \(y=2(x-0)+0=2x\)

Ищем расстояние между двумя параллельными прямыми: \(y=2x\) и \(y=2x-1\). Перпендикуляр из точки (0;0) на прямую \(y=2x-1\) имеет угловой коэффициент \(k=-\frac12\), его уравнение: \(y=-\frac12 x+b\). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и \(b=0\).

Уравнение перпендикуляра: \(y=-\frac x2\).
Находим точку пересечения прямой \(y=2x-1\) и перпендикуляра \(y=-\frac x2\): \begin 2x-1=-\frac x2\Rightarrow 2,5x=1\Rightarrow x=0,4;\ y=-\frac<0,4><2>=-0,2 \end Точка пересечения A(0,4;-0,2).
Находим расстояние \(OA=\sqrt<0,4^2+(-0,2)^2>=0,2\sqrt<2^2+1^2>=\frac<\sqrt<5>><5>\)
Ответ: \(\frac<\sqrt<5>><5>\)

10.3.1. Уравнение касательной

Выведем уравнение касательной к графику функции y=f (x) в точке с абсциссой х₀. Для наглядности используем график из 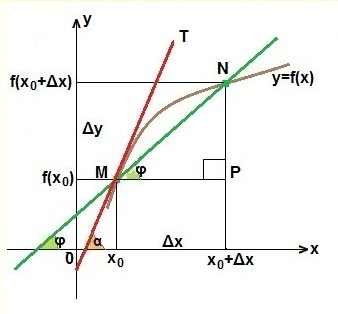предыдущего урока 10.3. («Определение производной. Геометрический смысл производной») и выведем уравнение касательной МТ.

Так как точку М мы взяли произвольно, то должны получить уравнение касательной, которое будет справедливо для любой функции y=f (x), имеющей касательную в определенной точке с абсциссой х₀.

Итак, любую прямую можно записать в виде y=kx+b, где k — угловой коэффициент прямой. Мы теперь знаем, что в качестве углового коэффициента можно взять f ‘(х₀) — значение производной функции y=f (x) в точке с абсциссой х₀. Эта точка является общей точкой для функции и для касательной МТ.

Таким образом, касательная МТ имеет вид: y=f ‘(х₀)·x+b. Осталось определить значение b. Это мы сделаем просто: подставим координаты точки М в последнее равенство, т.е. вместо х запишем х₀, а вместо у подставим f (х₀). Получаем равенство:

f (х₀) =f ‘(х₀)·х₀+b.

Отсюда b=f (х₀) — f ‘(х₀)·х₀. Подставляем это значение b в равенство: y=f ‘(х₀)·x+b. Тогда:

y =f ‘(х₀)·х+f (х₀) — f ‘(х₀)·х₀. Упростим.

y=f (х₀)+(f ‘(х₀)·х — f ‘(х₀)·х₀) или

y=f (х₀)+f ‘(х₀)(х — х₀). Это и есть искомое уравнение касательной МТ.

Выполнить следующие задания.

1. Написать уравнение касательной к графику функции y=x 2 в точке x₀=3. Сделать чертеж.

Решение.

Запишем уравнение касательной к графику функции y=f (x) в точке с абсциссой x₀ в общем виде:

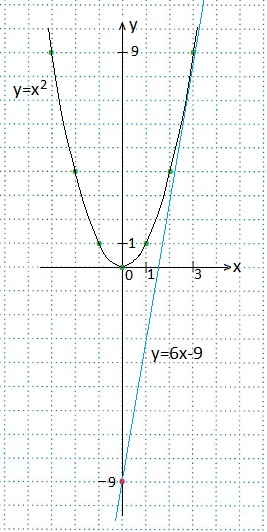
Находим значение данной функции в точке с данной абсциссой:

f (x₀)=f (3)=3 2 = 9 .

Находим производную f ‘(x)=(x 2 )’=2x и находим значение этой производной при х=3.

Тогда f ‘(x₀)=f ‘(3)=2·3= 6 .

Подставим найденные значения

f (x₀)= 9 и f ‘(x₀)= 6 в уравнение касательной, получим:

y= 9 + 6 ·(x-3);

y= 6 x-9 — искомое уравнение касательной.

Ответ: y= 6 x-9.

2. Написать уравнение касательной к графику функции

Решение.

Записываем общее уравнение касательной: y=f (x₀) +f ‘(x₀)(x-x₀). Находим значение данной функции в точке х=1, получаем:

f (x₀)=f (1) = 1 . Найдем производную данной функции по формуле производной степени:

f ‘(x)=(x -2 )=-2x -2-1 =-2x -3 .

Находим значение этой производной при х=1.

f ‘(x₀)=f (1)=-2·(1) -3 = -2 . Подставляем найденные значения в общее уравнение касательной:

y= 1 —2 (x-1);

y= -2 x+3 — искомое уравнение касательной.

Ответ: y=- 2 x+3.