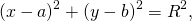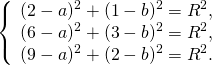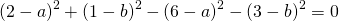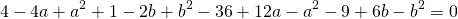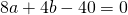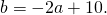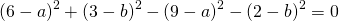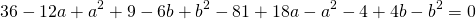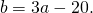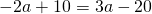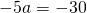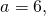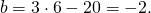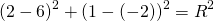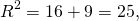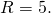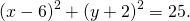Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Окружность, описанная около треугольника
Определение и формулы круга, описываемого вокруг треугольника
Круг, проходящий через все три вершины треугольника, называется его описанной окружностью.
Центр описанной окружности лежит на пересечении средних перпендикуляров к сторонам треугольника.
Круг может быть описан вокруг любого треугольника и только одного.
Радиус \(\ \mathrm
Радиус круга, описанного вокруг треугольника, равен отношению стороны треугольника к двойному синусу противоположного угла (следствие теоремы синуса):
В правом треугольнике центр описанной окружности лежит в середине гипотенузы.
Примеры решения проблем
Найти радиус окружности, описанной около треугольника \(\ \mathrm
Радиус \(\ R \) окружности, описываемой вокруг треугольника, найден из уравнения
Сумма углов произвольного треугольника равна \(\ 180^ <\circ>\) , поэтому
Теперь вы можете найти радиус окружности:
В треугольнике \(\ \mathrm
Радиус описанной окружности равен отношению стороны треугольника к двойному синусу противоположного угла
Из письменных равенств находим синусы углов B и C треугольника:
\(\ \sin \angle C=\frac<2 R>=\frac<8><8>=1, \sin \angle B=\frac<2 R>=\frac<6><8>=\frac<1> <2>\) откуда следует, что \(\ \angle C=90^ <\circ>\) и \(\ \angle B=30^ <\circ>\)
Написать уравнение окружности описанной около треугольника abc
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
 Серединный перпендикуляр к отрезку Серединный перпендикуляр к отрезку |
 Окружность описанная около треугольника Окружность описанная около треугольника |
 Свойства описанной около треугольника окружности. Теорема синусов Свойства описанной около треугольника окружности. Теорема синусов |
 Доказательства теорем о свойствах описанной около треугольника окружности Доказательства теорем о свойствах описанной около треугольника окружности |
Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника |  | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |  | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  |
Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
| l = 2Rsin φ . | (1) |
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
составить уравнение окружности описанной около треугольника abc если заданы координаты его
Составить уравнение окружности описанной около треугольника abc если заданы координаты его вершин a(0;3) b(4;0) c(4;3)
- Артём Званский
- Геометрия 2019-06-15 19:37:57 2 2
решение окончательно искривленное, но.
если расставить точки, то увидим прямоугольный треугольник=gt; АВ-гипотенуза тр-ка и поперечник окружности
обретаем центр АВ
получаем центр окр М(2;1,5)
R=AM= корень из (x2-x1)^2+(y2-y1)^2
AM=корень из (2-0)^2+(1,5-3)^2
АМ=корень из 4+2,25=корень из 6,25
получаем ур-е (х-2)^2+(y-1,5)^2=6,25
вектор ас имеет проекции
ас х = (4 — 0) = 4; ас у = (3 — 3) = 0
вектор bс имеет проекции
bс х = (4 — 4) = 0; bс у = (3 — 0) = 3
найдём скалярное творенье векторов ас и bс
ас bс = (4 0 + 0 3) = 0
следовательно векторы ас и вс перпендикулярны.
угол асв — прямой и опирается на поперечник аb
Найдём поперечник ав
IabI = (0 + 4) + (3 + 0) = 5
Радиус окружности равен половине поперечника R = 2,5.
Центр окружности O расположен посредине между точками а и b
Найдём координаты точки О
xО = (0 + 4)/2 = 2; уО = (3 + 0)/2 = 1,5
Запишем уравнение окружности (х — хО) + (у — уО) =R
http://www.homework.ru/spravochnik/okruzhnost-opisannaya-okolo-treugolnika/
http://b4.cooksy.ru/articles/napisat-uravnenie-okruzhnosti-opisannoy-okolo-treugolnika-abc