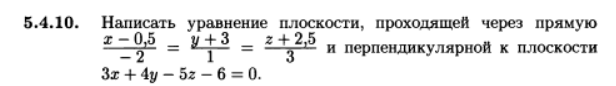Уравнение плоскости, проходящей через прямую перпендикулярно заданной плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости проходящей через прямую перпендикулярно заданной плоскости − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L
 . . | (1) |
 . . | (2) |
Пусть плоскость α1 не перпендинулярно прямой L.
Задача заключается в построении уравнения плоскости α, проходящей через прямую L перпендикулярно плоскости α1 (Рис.1).
 |
Запишем уравнение искомой плоскости α:
| Ax+By+Cz+D=0. | (3) |
Искомая плоскость α проходит через прямую L, следовательно она проходит через точку M0(x0, y0, z0). Тогда справедливо следующее равенство:
| Ax0+By0+Cz0+D=0. | (4) |
и поскольку прямая L принадлежит этой плоскости, то нормальный вектор n=<A, B, C> и направляющий вектор q=<m, p, l> ортогональны:
Для того, чтобы плоскость α была перпендикулярна плоскости α1, нормальные векторы этих плоскостей должны быть ортогональными, т.е. скалярное произведение этих векторов должно быть равным нулю:
| AA1+BB1+CC1=0 | (6) |
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
 | (7) |
Решив однородную систему линейных уравнений (7) найдем частное решение. (Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L перпендикулярно плоскости α1.
Пример 1. Найти уравнение плоскости α, проходящей через прямую L:
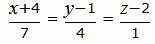 | (8) |
перпендикулярно плоскости α1 :
 | (9) |
Уравнение искомой плоскости α можно записать следующей формулой:
где n=<A, B, C> нормальный вектор плоскости.
Поскольку плоскость α проходит через прямую L , то она проходит также через точку M0(x0, y0, z0)=M0(−4, 1, 2), тогда уравнение плоскости должна удовлетворять условию:
| Ax0+By0+Cz0+D=0 | (10) |
а условие принадлежности прямой L к искомой плоскости α представляется следующим равенством:
| Am+Bp+Cl=0. | (11) |
Так как плоскость α должна быть перпендикулярна плоскости α1, то должна выполнятся условие:
| AA1+BB1+CC1=0 | (12) |
 | (13) |
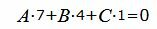 | (14) |
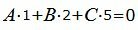 | (15) |
Представим эти уравнения в матричном виде:
 | (16) |
Решим систему линейных уравнений (16) отностительно A, B, C, D:
 | (17) |
Таким образом искомая плоскость имеет нормальный вектор n=<A, B, C>=<9/43,−17/43,5/43>. Тогда подставляя в уравнение плоскости
| Ax+By+Cz+D=0 | (18) |
значения A, B, C, D, получим:
 |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 43:
 | (19) |
Ответ: Уравнение плоскости, проходящей через прямую (1) перпендикулярно плоскости (2) имеет вид (19).
Пример 2. Найти уравнение плоскости α, проходящей через прямую L:
 | (20) |
перпендикулярно плоскости α1 :
 | (21) |
Уравнение искомой плоскости α можно записать следующей формулой:
где n=<A, B, C> нормальный вектор плоскости.
Так как плоскость α проходит через прямую L , то она проходит также через точку M0(x0, y0, z0)=M0(−3, 1, 5), тогда уравнение плоскости должна удовлетворять условию:
| Ax0+By0+Cz0+D=0 | (22) |
а условие принадлежности прямой L к искомой плоскости α представляется следующим равенством:
| Am+Bp+Cl=0. | (23) |
Так как плоскость α должна быть перпендикулярна плоскости α1, то должна выполнятся условие:
| AA1+BB1+CC1=0 | (24) |
 | (25) |
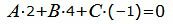 | (26) |
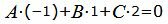 | (27) |
Представим эти уравнения в матричном виде:
 | (28) |
Решим систему линейных уравнений (28) отностительно A, B, C, D:
 | (29) |
Таким образом искомая плоскость имеет нормальный вектор n=<A, B, C>=<3/2,−1/2,1>. Тогда подставляя в уравнение плоскости
| Ax+By+Cz+D=0 | (30) |
значения A, B, C, D, получим:
 |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 43:
 | (31) |
Ответ: Уравнение плоскости, проходящей через прямую (1) перпендикулярно плоскости (2) имеет вид (31).
Задача 53930 уравнение плоскости проходящей через.
Условие
уравнение плоскости проходящей через прямую и перпендикулярна к плоскости
Решение
Каноническое уравнение плоскости
Ax+By+Cz+D=0
⇒ координаты нормального вектора плоскости vector
Значит из уравнения плоскости
3x+4y-5z-6=0
получаем vector
vector=(-2;1;3) — направляющий вектор прямой
P(0,5; -3;-2,5) — точка, лежащая на прямой и стало быть на искомой плоскости
Пусть М (x;y;z) — произвольная точка плоскости.
Условием компланарности трех векторов является равенство нулю определителя третьего порядка,
составленного из координат этих векторов
Раскрываем определитель:
5*(x-0,5)+9(y+2)-8*(z+2,5)-3*(z+2,5)-12(x-0,5)+10(y+2)=0
Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой
Данная статья дает представление о том, как составить уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Разберем приведенный алгоритм на примере решения типовых задач.
Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой
Пусть задано трехмерное пространство и прямоугольная система координат O x y z в нем. Заданы также точка М 1 ( x 1 , y 1 , z 1 ) , прямая a и плоскость α , проходящая через точку М 1 перпендикулярно прямой a . Необходимо записать уравнение плоскости α .
Прежде чем приступить к решению этой задачи, вспомним теорему геометрии из программы 10 — 11 классов, которая гласит:
Через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к заданной прямой.
Теперь рассмотрим, как же найти уравнение этой единственной плоскости, проходящей через исходную точку и перпендикулярной данной прямой.
Возможно записать общее уравнение плоскости, если известны координаты точки, принадлежащей этой плоскости, а также координаты нормального вектора плоскости.
Условием задачи нам заданы координаты x 1 , y 1 , z 1 точки М 1 , через которую проходит плоскость α . Если мы определим координаты нормального вектора плоскости α , то получим возможность записать искомое уравнение.
Нормальным вектором плоскости α , так как он ненулевой и лежит на прямой a , перпендикулярной плоскости α , будет являться любой направляющий вектор прямой a . Так, задача нахождения координат нормального вектора плоскости α преобразовывается в задачу определения координат направляющего вектора прямой a .
Определение координат направляющего вектора прямой a может осуществляться разными методами: зависит от варианта задания прямой a в исходных условиях. К примеру, если прямая a в условии задачи задана каноническими уравнениями вида
x — x 1 a x = y — y 1 a y = z — z 1 a z
или параметрическими уравнениями вида:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
то направляющий вектор прямой будет иметь координаты а x , а y и а z . В случае, когда прямая a представлена двумя точками М 2 ( x 2 , y 2 , z 2 ) и М 3 ( x 3 , y 3 , z 3 ) , то координаты направляющего вектора буду определяться как (x3 – x2, y3 – y2, z3 – z2).
Алгоритм для нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно заданной прямой:
— определяем координаты направляющего вектора прямой a : a → = ( а x , а y , а z ) ;
— определяем координаты нормального вектора плоскости α как координаты направляющего вектора прямой a :
n → = ( A , B , C ) , где A = a x , B = a y , C = a z ;
— записываем уравнение плоскости, проходящей через точку М 1 ( x 1 , y 1 , z 1 ) и имеющей нормальный вектор n → = ( A , B , C ) в виде A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 . Это и будет являться требуемым уравнением плоскости, которая проходит через заданную точку пространства и перпендикулярна к данной прямой.
Полученное общее уравнение плоскости: A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 дает возможность получить уравнение плоскости в отрезках или нормальное уравнение плоскости.
Решим несколько примеров, используя полученный выше алгоритм.
Задана точка М 1 ( 3 , — 4 , 5 ) , через которую проходит плоскость, и эта плоскость перпендикулярна координатной прямой О z .
Решение
направляющим вектором координатной прямой O z будет координатный вектор k ⇀ = ( 0 , 0 , 1 ) . Следовательно, нормальный вектор плоскости имеет координаты ( 0 , 0 , 1 ) . Запишем уравнение плоскости, проходящей через заданную точку М 1 ( 3 , — 4 , 5 ) , нормальный вектор которой имеет координаты ( 0 , 0 , 1 ) :
A ( x — x 1 ) + B ( y — y 1 ) + C ( z — z 1 ) = 0 ⇔ ⇔ 0 · ( x — 3 ) + 0 · ( y — ( — 4 ) ) + 1 · ( z — 5 ) = 0 ⇔ z — 5 = 0
Ответ: z – 5 = 0 .
Рассмотрим еще один способ решить данную задачу:
Плоскость, которая перпендикулярна прямой O z будет задана неполным общим уравнением плоскости вида С z + D = 0 , C ≠ 0 . Определим значения C и D : такие, при которых плоскость проходит через заданную точку. Подставим координаты этой точки в уравнение С z + D = 0 , получим: С · 5 + D = 0 . Т.е. числа, C и D связаны соотношением — D C = 5 . Приняв С = 1 , получим D = — 5 .
Подставим эти значения в уравнение С z + D = 0 и получим требуемое уравнение плоскости, перпендикулярной к прямой O z и проходящей через точку М 1 ( 3 , — 4 , 5 ) .
Оно будет иметь вид: z – 5 = 0 .
Ответ: z – 5 = 0 .
Составьте уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой x — 3 = y + 1 — 7 = z + 5 2
Решение
Опираясь на условия задачи, можно утверждать, что за нормальный вектор n → заданной плоскости можно принять направляющий вектор заданной прямой. Таким, образом: n → = ( — 3 , — 7 , 2 ) . Запишем уравнение плоскости, проходящей через точку О ( 0 , 0 , 0 ) и имеющей нормальный вектор n → = ( — 3 , — 7 , 2 ) :
— 3 · ( x — 0 ) — 7 · ( y — 0 ) + 2 · ( z — 0 ) = 0 ⇔ — 3 x — 7 y + 2 z = 0
Мы получили требуемое уравнение плоскости, проходящей через начало координат перпендикулярно к заданной прямой.
Ответ: — 3 x — 7 y + 2 z = 0
Задана прямоугольная система координат O x y z в трехмерном пространстве, в ней – две точки А ( 2 , — 1 , — 2 ) и B ( 3 , — 2 , 4 ) . Плоскость α проходит через точку A перпендикулярно прямой А В . Необходимо составить уравнение плоскости α в отрезках.
Решение
Плоскость α перпендикулярна к прямой А В , тогда вектор А В → будет нормальным вектором плоскости α . Координаты этого вектора определяются как разности соответствующих координат точек В ( 3 , — 2 , 4 ) и А ( 2 , — 1 , — 2 ) :
A B → = ( 3 — 2 , — 2 — ( — 1 ) , 4 — ( — 2 ) ) ⇔ A B → = ( 1 , — 1 , 6 )
Общее уравнение плоскости будет записано в следующем виде:
1 · x — 2 — 1 · y — ( — 1 + 6 · ( z — ( — 2 ) ) = 0 ⇔ x — y + 6 z + 9 = 0
Теперь составим искомое уравнение плоскости в отрезках:
x — y + 6 z + 9 = 0 ⇔ x — y + 6 z = — 9 ⇔ x — 9 + y 9 + z — 3 2 = 1
Ответ: x — 9 + y 9 + z — 3 2 = 1
Также нужно отметить, что встречаются задачи, требование которых – написать уравнение плоскости, проходящей через заданную точку и перпендикулярной к двум заданным плоскостям. В общем, решение этой задачи в том, чтобы составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, т.к. две пересекающиеся плоскости задают прямую линию.
Задана прямоугольная система координат O x y z , в ней – точка М 1 ( 2 , 0 , — 5 ) . Заданы также уравнения двух плоскостей 3 x + 2 y + 1 = 0 и x + 2 z – 1 = 0 , которые пересекаются по прямой a . Необходимо составить уравнение плоскости, проходящей через точку М 1 перпендикулярно к прямой a .
Решение
Определим координаты направляющего вектора прямой a . Он перпендикулярен как нормальному вектору n 1 → ( 3 , 2 , 0 ) плоскости n → ( 1 , 0 , 2 ) , так и нормальному вектору 3 x + 2 y + 1 = 0 плоскости x + 2 z — 1 = 0 .
Тогда направляющим вектором α → прямой a возьмем векторное произведение векторов n 1 → и n 2 → :
a → = n 1 → × n 2 → = i → j → k → 3 2 0 1 0 2 = 4 · i → — 6 · j → — 2 · k → ⇒ a → = ( 4 , — 6 , — 2 )
Таким образом, вектор n → = ( 4 , — 6 , — 2 ) будет нормальным вектором плоскости, перпендикулярной к прямой a . Запишем искомое уравнение плоскости:
4 · ( x — 2 ) — 6 · ( y — 0 ) — 2 · ( z — ( — 5 ) ) = 0 ⇔ 4 x — 6 y — 2 z — 18 = 0 ⇔ ⇔ 2 x — 3 y — z — 9 = 0
Ответ: 2 x — 3 y — z — 9 = 0
http://reshimvse.com/zadacha.php?id=53930
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-prohodjaschej-cherez-zadannuju/