Написать уравнение плоскости содержащей прямые

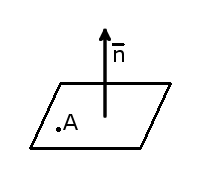
Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые.

В этой статье собрана информация, необходимая для нахождения уравнения плоскости, проходящей через две заданные пересекающиеся или параллельные прямые. Сначала разобран принцип составления уравнения плоскости, которая проходит через две заданные прямые, после этого приведены подробные решения характерных примеров.

Навигация по странице.

Нахождение уравнения плоскости, проходящей через две пересекающиеся прямые.

Прежде чем приступать к нахождению уравнения плоскости, проходящей через две заданные пересекающиеся прямые, напомним одну теорему: в трехмерном пространстве через две пересекающиеся прямые проходит единственная плоскость. Это утверждение является следствием из двух аксиом геометрии:

• через три различные и не лежащие на одной прямой точки проходит единственная плоскость;
• если две несовпадающие точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Таким образом, конкретную плоскость в трехмерном пространстве можно задать, указав две пересекающиеся прямые, лежащие в этой плоскости.

Теперь покажем, что плоскость, проходящая через две заданные пересекающиеся прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных прямых, а третья – на другой прямой.

Пусть заданные прямые a и b пересекаются в точке М . Отметим на прямой a две различные точки М₁ и М₂ (одна из них может совпадать с точкой M ), а на прямой b точку М₃ , отличную от точки М . Покажем, что плоскость М₁М₂М₃ есть плоскость, проходящая через заданные пересекающиеся прямые a и b .

Так как в плоскости М₁М₂М₃ лежат две точки прямой a (точки М₁ и М₂ ), то из озвученной в начале этого пункта аксиомы следует, что все точки прямой a лежат в плоскости М₁М₂М₃ , в частности, точка М . Тогда в плоскости М₁М₂М₃ лежат все точки прямой b , так как две несовпадающие точки прямой b (точки М и М₃ ) лежат в указанной плоскости. Следовательно, плоскость, проходящая через пересекающиеся прямые a и b , и плоскость, проходящая через три точки М₁ , М₂ и М₂ , совпадают.

Итак, поставим перед собой следующую задачу.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , заданы две пересекающиеся прямые a и b , и требуется написать уравнение плоскости, проходящей через пересекающиеся прямые a и b .

Сведем решение этой задачи к нахождению уравнения плоскости, проходящей через три точки. Для этого нужно определить координаты двух различных точек M₁ и M₂ , лежащих на одной из заданных пересекающихся прямых, и координаты точки M₃ , лежащей на другой прямой и не являющейся точкой пересечения заданных прямых. Для нахождения координат точек М₁ , М₂ и М₃ все средства хороши. Например, можно получить параметрические уравнения прямой a в пространстве вида . Из них видны координаты точки М₁ (они получаются при ), а координаты точки М₂ можно вычислить, придав параметру любое ненулевое действительное значение (к примеру, ). После этого можно получить параметрические уравнения прямой b и при некотором значении параметра вычислить координаты точки М₃ , не забыв удостовериться, что она не является точкой пересечения заданных прямых (что она не лежит на прямой a ).

Будем считать, что координаты точек М₁ , М₂ и М₃ найдены. После этого мы можем написать уравнение плоскости, проходящей через три точки и в виде . Вычислив определитель матицы вида , мы получим общее уравнение плоскости М₁М₂М₃ , которое и будет уравнением плоскости, проходящей через две пересекающиеся прямые a и b .

Нахождение уравнения плоскости, проходящей через две параллельные прямые.

Прежде чем получить уравнение плоскости, проходящей через две заданные параллельные прямые, вспомним теорему: через две параллельные прямые проходит единственная плоскость. Эта теорема доказывается на основе аксиомы о единственной плоскости, проходящей через три заданные точки, с использованием утверждения: если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Таким образом, мы можем задать конкретную плоскость в трехмерном пространстве, указав две параллельные прямые, лежащие в этой плоскости.

Очевидно, что плоскость, проходящая через две заданные параллельные прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных параллельных прямых, а третья лежит на другой прямой.

Теперь можно приступать к нахождению уравнения плоскости, проходящей через две заданные параллельные прямые.

Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , заданы две параллельные прямые a и b и требуется составить уравнение плоскости, которая проходит через параллельные прямые a и b .

Эта задача, также как и задача о нахождении уравнения плоскости, проходящей через две заданные пересекающиеся прямые, сводится к составлению уравнения плоскости, проходящей через три точки. Действительно, мы можем определить координаты двух точек М₁ и М₂ , лежащих на одной из заданных параллельных прямых, и координаты точки М₃ , лежащей на другой прямой. После этого нам лишь нужно написать уравнение плоскости, проходящей через три точки и , в виде . Это уравнение является искомым уравнением плоскости, проходящей через две заданные параллельные прямые.

Примеры составления уравнения плоскости, проходящей через две прямые.

Итак, чтобы написать уравнение плоскости, проходящей через две заданные параллельные или пересекающиеся прямые, нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки. Покажем применение этого алгоритма при решении примеров.

Известно, что прямая a в прямоугольной системе координат Oxyz в трехмерном пространстве проходит через точку и пересекает координатную прямую Oy в точке . Напишите уравнение плоскости, проходящей через пересекающиеся прямые a и Oy .

Из условия нам известны координаты двух точек М₁ и М₂ , лежащих на прямой a . Очевидно, что точка лежит на координатной прямой Oy и не совпадает с точками М₁ и М₂ . Тогда плоскость, проходящая через три точки , и , есть плоскость, проходящая через пересекающиеся прямые a и Oy . Напишем ее уравнение:

.

Рассмотрим еще один пример, в котором координаты точек, лежащих на заданных пересекающихся прямых, не так очевидны.

Составьте уравнение плоскости, которая проходит через две пересекающиеся прямые a и b , заданные уравнениями и соответственно.

Сначала найдем координаты двух точек, лежащих на прямой a , и координаты точки, лежащей на прямой b .

Прямая, которую в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида , проходит через точку . Перейдем к параметрическим уравнениям этой прямой, чтобы определить координаты еще одной точки (обозначим ее М₂ ), лежащей на ней. Имеем , примем и из параметрических уравнений прямой вычислим координаты точки М₂ : . Следовательно, .

Очевидно, что прямая проходит через точку . Проверим, не является ли точка точкой пересечения заданных прямых, подставив ее координаты в уравнения прямой a : . Канонические уравнения прямой a обратились в тождества, следовательно, точка М₃ лежит на прямой a и является точкой пересечения заданных прямых. Таким образом, нам нужно взять другую точку М₃ , лежащую на прямой b , так как сейчас найденные точки М₁ , М₂ и М₃ лежат на одной прямой. Для этого мы также переходим к параметрическим уравнениям прямой b : , и вычисляем координаты точки М₃ , приняв : .

Теперь мы можем получить уравнение плоскости, проходящей через три точки , и , которое является искомым уравнением плоскости, проходящей через две заданные пересекающиеся прямые:

.

Не правда ли, что нахождение координат точек, лежащих на заданных прямых, является самым трудоемким процессом при составлении уравнения плоскости, проходящей через две пересекающиеся прямые?

Осталось рассмотреть пример составления уравнения плоскости, проходящей через две заданные параллельные прямые.

Напишите уравнение плоскости, проходящей через две параллельные прямые и .

По параметрическим уравнениям прямой при и вычислим координаты двух точек М₁ и М₂ :

Очевидно, что прямая проходит через точку .

Найдем уравнение плоскости, проходящей через три точки М₁ , М₂ и М₃ :

Это уравнение и есть искомое уравнение плоскости, проходящей через две заданные параллельные прямые.

.

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Уравнение плоскости, проходящей через точку и прямую онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:

.

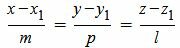(1)

Задача заключается в построении уравнения плоскости α, проходящей через точку M₀ и и через прямую L(Рис.1).

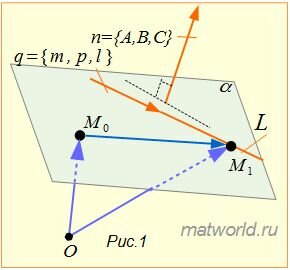Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:

Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M₁(x₁, y₁, z₁). Тогда уравнение плоскости, проходящей через точку M₁(x₁, y₁, z₁) имеет вид:

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:

Вычитая уравнение (3) из уравнения (2), получим:

Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M₀ и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:

.

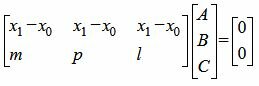(6)

Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.

Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.

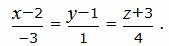(7)

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀)=M₀(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).

Вычитая уравнение (3) из уравнения (2), получим:

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:

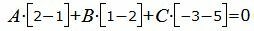(10)

(11)

Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:

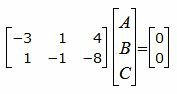(12)

Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:

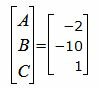Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:

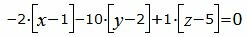(13)

Упростим уравнение (13):

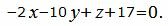(14)

Ответ: Уравнение плоскости, проходящей через точку M₀(1, 2, 5) и через прямую (7) имеет вид (14).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и через прямую L, заданной параметрическим уравнением:

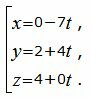(15)

Решение. Приведем параметрическое уравнение (15) к каноническому виду:

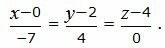(16)

Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n=<A, B, C> представляется формулой:

Поскольку плоскость проходит через прямую L, то она проходит также через точку M₁(x₁, y₁, z₁)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M₁(x₁, y₁, z₁) имеет вид:

Вычитая уравнение (18) из уравнения (17), получим:

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :

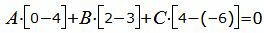(21)

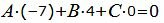(22)

Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:

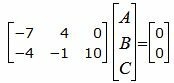(23)

Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:

Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:

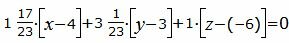(24)

Упростим уравнение (24):

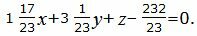(25)

Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.

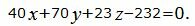(26)

Ответ: Уравнение плоскости, проходящей через точку M₀(4, 3, −6) и через прямую (16) имеет вид (26).