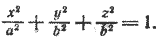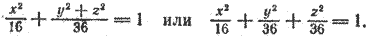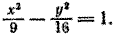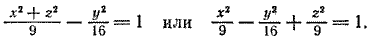Написать уравнение поверхности вращением кривой

Глава VI. Простейшие криволинейные поверхности и тела вращения.

§ 75*. Поверхности вращения

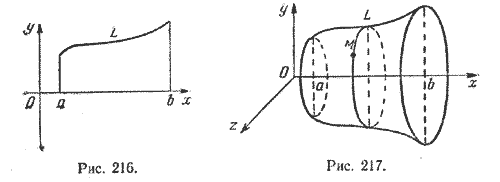
1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.

Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение

y = f(x), х [а; b]. (1)

Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).

Очевидно, точка M с координатами (х; у; z), где х [а; b], принадлежит искомой поверхности вращения тогда и только тогда, когда

Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).

Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид

y 2 + z 2 = (f(x)) 2 , х [а; b]. (2)

Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,

В частности, если кривая L задана уравнением

то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид

т. е. просто y 2 заменяем на y 2 + z 2 .

2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.

Пусть в плоскости хОу эллипс задан уравнением

(5)

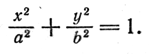
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим

(6)

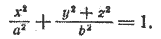
Это уравнение обычно записывают так:

При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:

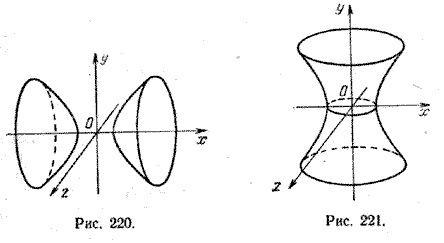
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).

Пусть в плоскости хОу гипербола задана уравнением

(7)

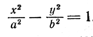
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим

(8)

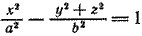
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим

(9)

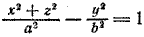
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.

Составим уравнение гиперболы:

Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим

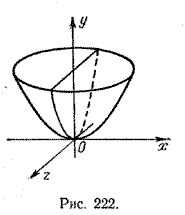
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).

Пусть на плоскости хОу парабола задана уравнением

Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим

Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.

Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).

Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.

Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим

5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.

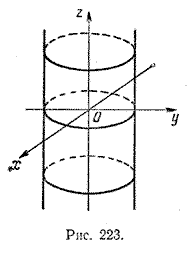
Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение

Эта цилиндрическая поверхность изображена на рис. 223.

Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.

В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим

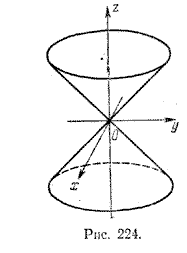
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.

Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид

Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).

Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.

Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.

VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Линейчатые поверхности. Поверхности вращения

Краткие теоретические сведения

Поверхность, допускающая параметризацию вида: \begin \vec=\vec<\rho>(u)+v\vec<\mu>(u), \end где $\vec<\rho>$, $\vec<\mu>$ — гладкие вектор-функции, называется линейчатой. $u=\mbox$ называется образующей (образующая имеет направляющий вектор $\vec<\mu>(u)$), $\vec<\rho>=\vec<\rho>(u)$ называется направляющей.

Линейчатая поверхность — поверхность, описанная движением прямой, называемой образующей, пересекающей при движении некоторую кривую, называемую направляющей поверхности.

Рассмотрим два вида линейчатой поверхности — цилиндрическая и коническая.

Цилиндрическая поверхность:
Направляющая: $\vec<\rho>=\vec<\rho>(u)$,
Образующая: постоянный единичный вектор $\vec<\mu>=\vec$. \begin \vec=\vec<\rho>(u)+v\vec. \end

Коническая поверхность:
Вершина в точке $M(\vec<\rho>_0)$,
Направляющая: $\vec<\rho>=\vec<\rho>(u)$,
Образующая: $\vec<\mu>=\vec<\rho>(u)-\vec<\rho>_0$. \begin \vec=\vec<\rho>_0+v(\vec<\rho>(u)-\vec<\rho>_0). \end

Описанные линейчатые поверхности являются развертывающимися, то есть их касательные плоскости остаются неизменными вдоль прямолинейной образующей.

Еще один пример развертывающейся поверхности — поверхность, образованная касательными к некоторой кривой.

Из сказанного выше следует, что совокупность всех касательных плоскостей развертывающейся линейчатой поверхности представляет собой однопараметрическое семейство, то есть развертывающаяся линейчатая поверхность является огибающей однопараметрического семейства плоскостей.

Поверхность вращения — поверхность, образованная при вращении некоторой кривой около оси. Линии пересечения поверхности с плоскостями, проходящими через ось вращения, называются \emph<меридианами>, а линии пересечения с плоскостями, перпендикулярными оси, называются \emph<параллелями>.

Уравнение поверхности вращения, которая образуется при вращении кривой \begin x=x(u), \,\, z=z(u), \,\, x\geqslant0 \end расположенной в плоскости $(xz)$, вокруг оси $Oz$: \begin x=x(u)\,\mbox\,v, \,\, y= x(u)\,\mbox\,v, \,\, z=z(u). \end

Решение задач

Задание 1 (Феденко 535)

Написать уравнение цилиндрической поверхности, для которой линия $\vec<\rho>=\vec<\rho>(u)$ является направляющей, а образующие параллельны вектору $\vec$. \begin \vec=\vec<\rho>(u)+v\vec. \end

Задание 2 (Феденко 536)

Напишите параметрические уравнения цилиндрической поверхности, образующие которой параллельны вектору $\vec=\<1,2,3\>$, а направляющая задана уравнениями: $x=u$, $y=u^2$, $z=u^3$.

Задание 3 (Феденко 534)

Напишите параметрические уравнения гиперболического и параболического цилиндров.

Для параболического цилиндра — самостоятельно.

Задание 4 (Феденко 541)

Задана точка $M(a,b,c)$ и линия $L$: \begin x=f(u), \,\, y=\varphi(u), \,\, z=\psi(u). \end Напишите в параметрическом и неявном виде уравнения конуса с вершиной в точке $M$ и с направляющей линией $L$.

Задание 5

Составьте параметрическое и неявное уравнения конуса, образуемого прямыми, проходящими через точку $M(1,1,1)$ и пересекающими эллипс: \begin x=a\,\mbox\,u, \,\, y=b\,\mbox\,u, \,\, z=0. \end

Задание 6 (Феденко 529)

Напишите уравнение тора, который получается при вращении окружности \begin x=a+b\,\mbox\,u, \,\, y=0 , \,\, z=b\,\mbox\,u \,\, (b