Написать уравнение прямой проходящей через середину отрезка

аписать уравнение прямой, проходящей через точку А (-2;8) и середину отрезка MN, где М (6; -5), N (-2; 1), используя каноническое уравнение.

Координаты середины векторов вычисляются по формуле:

— где C — координата середины, К — конца, Н — начала:
Пусть середина MN — С, тогда:

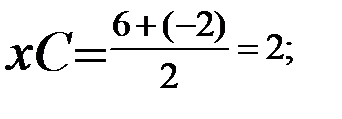
Данные точки лежат на одной прямой. Через систему уравнений найдём коэффициенты k и b данной прямой y=kx+b, подставив в неё координаты точек:

8 = -2k+b 8 = -2k-2-2k 4k =-10 k = -2,5

-2 = 2k+b b = -2-2k b =-2-2k b = 3

Для полученной прямой y = -2,5x+3 приведём уравнение:

2. Найти пределы:

а) б)

а) = = =

= = = 2

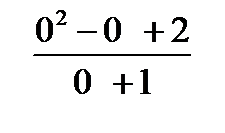
б) =

Разделим числитель и знаменатель на х 3

= =

Сделаем замену: u=1/x

= = = —

3. Найти интегралы:

а) ; б) ; в) .

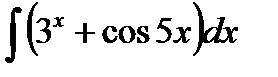
а) = — + = — + 3x + C

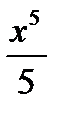
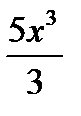
б) = 8 = 8 ln x + C

в) = + = +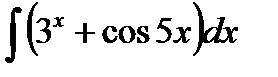

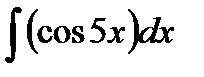
Тогда пусть du=5dx и подставим dx=du/5:

+ = + = + sin(u)+C= + sin(5x)+C

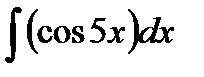
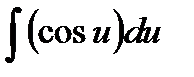
4. Исследовать функцию и построить график: у = 3х 3 – х

Точки пересечения с осью координат Y

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в 3х 3 – х.
3⋅ 0 3 − 0=0

Точки пересечения с осью координат X

График пересекает ось X, когда y равняется 0:
подставляем y = 0 в y=3x 3 — x.
3 x 3 −x =0

x₂=

x₃=-

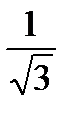
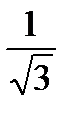
Точки: (0, 0); ( ,0); ( — ,0).

Для того, чтобы найти экстремумы, нужно решить уравнение
f ′(x)=0 (производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
f ′(x)=( 3 x 3 −x)′ = 9x 2 – 1
9x 2 – 1 = 0

Решаем это уравнение, получаем:

x₁=− ;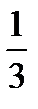

x₂= .

Значит экстремумы в точках: (− ; ); ( ; — )

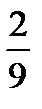
Интервалы возрастания и убывания функции.
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимум функции в точке x₁= ;
Максимум функции в точке x₂=− .

Убывает на промежутках ( — ∞; − ] U [∞; )
Возрастает на промежутке [− ; ]

Найдем точки перегибов, для этого надо решить уравнение

f ′′(x)=0 (вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции,
f ′′(x)= (3 x 3 −x)′′= (9x 2 – 1)′ = 18x

Решаем это уравнение, получаем:

Интервалы выпуклости и вогнутости.
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
[0, ∞)
Выпуклая на промежутках
(-∞, 0]

Горизонтальные асимптоты найдём с помощью пределов данной функции при x→∞ и x→ — ∞
(3x 3 -x)= — ∞ значит,
горизонтальной асимптоты слева не существует.
(3x 3 -x)= ∞ значит,
горизонтальной асимптоты справа не существует.

Наклонную асимптоту можно найти, подсчитав предел функции 3x 3 -x, делённой на x при x→∞ и x→ — ∞
= ∞ значит,
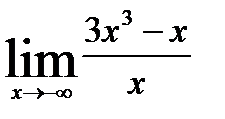
наклонной асимптоты слева не существует.
= ∞ значит,
наклонной асимптоты справа не существует.

Чётность и нечётность функции

Проверим чётность и нечётность функции с помощью соотношений

f = f(-x) и f = -f(-x).
Итак, проверяем:
3x 3 -x = -3x 3 +x Нет

3x 3 -x = -(-3x 3 +x) Нет
значит, функция не является ни чётной, ни нечётной.

5.Решить дифференциальное уравнение:

у(0)=5

Представим исходное дифференциальное уравнение в виде:

или

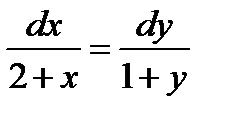
Интегрируя обе части, получаем:

Тогда решением дифференциального уравнения будет

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная система координат O x y .

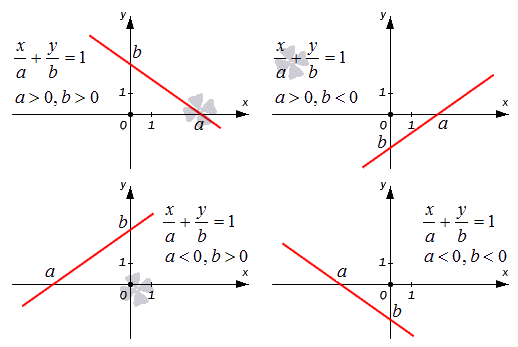
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.

На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

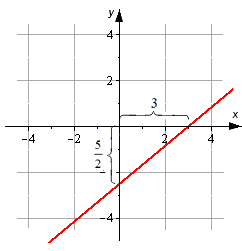
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .

Решение

Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .

В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .

Разберем следующий пример.

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .

Решение

Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Мы получили уравнение прямой в отрезках.

Ответ: x — 1 2 + y 1 14 = 1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .

x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0

Ответ: 3 2 · x — 1 12 · y — 1 = 0

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?

Геометрия | 5 — 9 классы

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7).

Прямая — график линейной функции, то есть y = kx + b.

Так как искомаяпрямая проходит параллельно прямой y = 2x + 5, то их угловые коэфициенты равны.

Середина отрезка AB — точка O.

Найдем ее координаты :

x = (xA + xB) / 2 = (2 + 0) / 2 = 1

y = (yA + yB) / 2 = ( — 1 + 7) / 2 = 3

Найдем b, для этого подставим координаты точки O :

значит искомое уравнение прямой — y = 2x + 1.

Отрезки АВ и CD пересекаются в их общей середине?

Отрезки АВ и CD пересекаются в их общей середине.

Докажите, что прямые АС и BD параллельны.

) Вершины В и С треугольника АВС лежат в плоскости \ beta ?

) Вершины В и С треугольника АВС лежат в плоскости \ beta .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости \ beta .

1) Вершины В и С треугольника АВС лежат в плоскости ?

1) Вершины В и С треугольника АВС лежат в плоскости .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости .

Концы отрезка АВ лежат на параллельных прямых a и b?

Концы отрезка АВ лежат на параллельных прямых a и b.

Прямая, проходящая через середину О этого отрезка , пересекает прямые a и b в точках С и D.

Докажите что СО = ОD.

Отрезки АВ и СD пересекаются в их общей середине?

Отрезки АВ и СD пересекаются в их общей середине.

Докажите, что прямые AC и BD параллельны.

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой?

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой.

Докажите параллельность прямых АС и ВD.

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми?

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми.

Перпендикулярные отрезки KN и PM пересекаются в их общей середине?

Перпендикулярные отрезки KN и PM пересекаются в их общей середине.

Начертите прямую, проходящую через точку К, параллельную прямой, содержащей отрезок PM.

⦁Отрезки АС и BD пересекаются в их общей середине точке О?

⦁Отрезки АС и BD пересекаются в их общей середине точке О.

Докажите, что прямые АВ и CD параллельны.

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку?

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

180 * 5 (т. К. 5 треугольников).

Так как сумма всех углов треугольника равна 180 * , а в равнобедренном треугольнике углы при основании равны, следовательно углы при основании равны (180 * — 80 * ) / 2 = 50 *.

1) два угла у которых одна сторона общая а два другие являются продолжениями друг — друга, 2)сумма смежных углов равна 180, получается, что если узнать один угол, нужно из 180 вычесть известный угол и узнаем второй 4) острый — угол меньше 90 градусов..

2) думаю потому что если провести в ромбе ось симметрии, то одна часть будет симметрична второй в перевернутом виде. Нарисуйте, думаю, все понятно сразу станет. Удачи).

1. Используем теорему Особые прямоугольные треугольники. Если один угол 60° другой 30°. То отношения сторон равна 1 : корень 3 : 2 гипотенуза 8 то один из катетов 8÷2 = 4 а другой 4 под корень 3 2. Это так же как 1 — ое задания гипотенуза — 30 оди..

1) угол лежащий против 30 градусов равен 1 / 2 гипотенузы = 4 а там по теореме пифагора.

Докажите что отрезки соединяющие середины противоположных сторон произвольного четырехугольника точкой пересечения делятся пополам. Докажите через векторы. Не заметил последнее предложение. Поэтому получилось, что доказал двумя способами.

AC(3 — 2 ; 1 — 8) = (1 ; — 7) AB( — 1 — 2 ; 5 — 8) = ( — 3 ; — 3) AC — 2AB = (1 — 2 * ( — 3) ; — 7 — 2 * ( — 3)) = (7 ; — 1) BC(4 ; — 4) AB * BC = ( — 3) * 4 + ( — 3) * ( — 4) = — 12 + 12 = 0 CA( — 7 ; 1) AB * CA = ( — 3) * ( — 7) + ( — 3) * 1 = 21 -..

1) Пусть один угол х, тогда другой х + 50 х + х + 50 = 180 2х = 130 х = 75° — меньший угол 1) 75 + 50 = 125° — больший угол.

ВС = АВ — АС ВС = 9, 2 — 2, 4 между АВ лежит точка С.