Написать уравнение вектора проходящего через точку

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

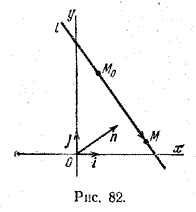
Пусть дана некоторая точка М₀ и вектор n. Проведем через точку М₀ прямую l перпендикулярно вектору n (рис. 82).

Пусть M — произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор \(\overrightarrowM>\) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и \(\overrightarrowM>\) равнялось нулю:

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M₀ и M имеют координаты (x₀ ; у₀ ) и (x; у).

Тогда \(\overrightarrowM>\) = (x — x₀; у — у₀). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:

Уравнение (2) есть уравнение прямой l, проходящей через данную точку М₀ (x₀; у₀) перпендикулярно данному вектору n = (А; В).

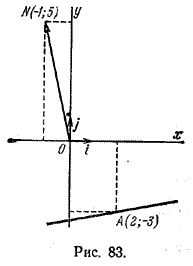
Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).

Пользуясь формулой (2), находим уравнение данной прямой:

— 1 • (x-2) + 5 • (у + 3) = 0

или, окончательно, x — 5у — 17 = 0.

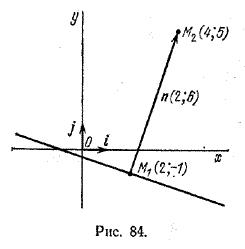
Задача 2. Даны точки M₁(2; -1) и M₂(4; 5). Написать уравнение прямой, проходящей через точку М₁ перпендикулярно вектору \(\overrightarrowM_<2>>\).

Нормальный вектор искомой прямой n = \(\overrightarrowM_<2>>\) имеет координаты (2; 6) (рис. 84).

Следовательно, по формуле (2) получим уравнение

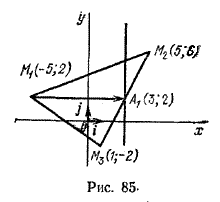
Задача 3. В треугольнике с вершинами в точках M₁(-5; 2), M₂(5; 6) и M₃(1; -2) проведена медиана M₁А₁. Требуется составить уравнение прямой, проходящей через точку А₁ перпендикулярно медиане M₁A₁ (рис. 85).

За нормальный вектор искомой прямой можно принять вектор n = \(\overrightarrowA_<1>>\). Определим его координаты. Точка A₁ — середина отрезка M₂M₃, поэтому, если (x₁; y₁) — ее координаты, то \( x_1 = \frac<5+1><2>=3, \;\;а \;\; y_1=\frac<6-2><2>=2 \).

Тогда нормальный вектор n = \(\overrightarrowA_<1>>\) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид

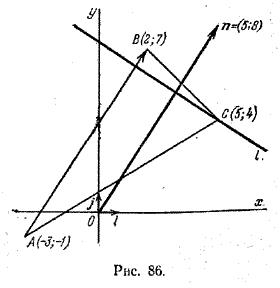
Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).

За нормальный вектор искомой прямой можно взять вектор n = \(\overrightarrow\).

Так как n = (2-(-3); 7 — (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

или, окончательно, 5х + 8у — 57 = 0.

Уравнения прямой, проходящей через точку коллинеарно вектору

Параметрическое уравнение прямой

Направляющим вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.

Пусть на координатной плоскости заданы точка и ненулевой вектор (рис. 3.13). Требуется составить уравнение прямой, коллинеарной вектору и проходящей через точку .

Выберем на прямой произвольную точку . Обозначим и — радиус-векторы точек и (рис.3.14).

Точка принадлежит заданной прямой тогда и только тогда, когда векторы и коллинеарны. Запишем условие коллинеарности : , где — некоторое действительное число (параметр). Учитывая, что , получим векторное параметрическое уравнение прямой :

где — направляющий вектор прямой, а — радиус-вектор точки, принадлежащей прямой.

Координатная форма записи уравнения (3.11) называется параметрическим уравнением прямой

где — координаты направляющего вектора прямой. Параметр в уравнениях (3.11),(3.12) имеет следующий геометрический смысл : величина пропорциональна расстоянию от начальной точки до точки . Физический смысл параметра в параметрических уравнениях (3.11), (3.12) — это время при равномерном и прямолинейном движении точки по прямой. При точка совпадает с начальной точкой , при возрастании движение происходит в направлении, определяемым направляющим вектором .

Каноническое уравнение прямой

Выразим параметр из каждого уравнения системы (3.12): , а затем исключим этот параметр:

Уравнение (3.13) называется каноническим уравнением прямой . В этом уравнении коэффициенты и не равны нулю одновременно, так как это координаты направляющего вектора прямой.

1. Если один из знаменателей дробей в (3.13) равен нулю, то считается, что соответствующий числитель дроби равен нулю:

– каноническое уравнение – это уравнение прямой , параллельной оси ординат (рис.3.15,а);

– каноническое уравнение — это уравнение прямой , параллельной оси абсцисс (рис.3.15,6).

2. Поскольку направляющий вектор коллинеарен прямой, а нормаль ей перпендикулярна, то векторы и ортогональны. Следовательно, их скалярное произведение равно нулю:

т.е. координаты направляющего вектора прямой и ее нормали связаны однородным уравнением: . Подставим, например, решение этого уравнения в общее уравнение прямой (3.7):

Это соотношение позволяет по координатам направляющего вектора и координатам точки записать уравнение прямой без промежуточных вычислений.

3. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор , где , также является направляющим вектором для той же прямой.

4. Для перехода от общего уравнения прямой (3.8) к каноническому (3.13) нужно выполнить следующие действия:

1) найти любое решение уравнения , определяя тем самым координаты точки , принадлежащей прямой;

2) найти любое ненулевое решение однородного уравнения , определяя тем самым координаты направляющего вектора , в частности, можно взять ;

3) записать каноническое уравнение (3.13).

5. Чтобы перейти от канонического уравнения к общему , достаточно перенести все члены уравнения (3.13) в левую часть:

Полученное уравнение (при ) имеет вид (3.8) с .

6. Чтобы перейти от канонического уравнения к параметрическому , следует приравнять левую и правую части уравнения (3.13) параметру и записать полученное двойное равенство в виде системы (3.12):

7. Параметрическое (3.12) и каноническое (3.13) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.

Пример 3.8. На координатной плоскости (в прямоугольной системе координат) заданы прямая и точка (рис.3.16). Требуется:

а) Нормаль к прямой является направляющим вектором для прямой . Координаты нормали определяем по общему уравнению прямой , тогда , . Составляем параметрическое уравнение (3.12) прямой :

б) Проекция точки является точкой пересечения прямых и . Найдем ее координаты. Для этого подставляем в уравнение прямой выражения координат и из параметрического уравнения прямой . Получим уравнение

Значению параметра отвечает точка с координатами и . Следовательно, искомая точка .

в) В пункте «а» составлено параметрическое уравнение прямой . В этом уравнении при получаем точку , при — точку , значит искомую точку получим при , поскольку в силу симметрии . Вычисляем координаты искомой точки:

Пример 3.9. На координатной плоскости (в прямоугольной системе координат) заданы вершины треугольника (рис.3.17). Составить:

а) каноническое уравнение прямой, содержащей высоту треугольника;

б) каноническое и параметрическое уравнения прямой, содержащей биссектрису треугольника.

а) В примере 3.7 было получено общее уравнение прямой . Перейдем от общего уравнения к каноническому.

1) Найдем любое решение уравнения , например, и (точкам принадлежит прямой ).

2) Найдем ненулевое решение однородного уравнения , например (направляющий вектор прямой имеет координаты ).

3) Запишем каноническое уравнение: .

б) Найдем направляющий вектор биссектрисы . Для этого отложим от вершины единичные векторы и построим на них ромб (изображенный на рис.3.17 штриховой линией). Поскольку диагональ ромба является биссектрисой, то вектор . является направляющим вектором биссектрисы . Находим координаты и длины векторов:

Составляем каноническое уравнение прямой с направляющим вектором , проходящей через точку :

Чтобы получить параметрическое уравнение прямой , приравниваем левую и правую части канонического уравнения параметру . Записываем полученную систему в виде

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

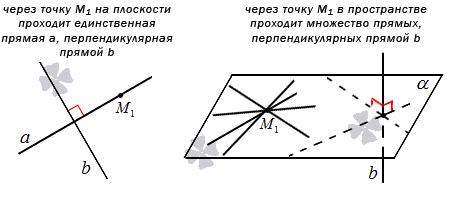
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .