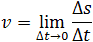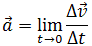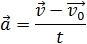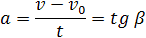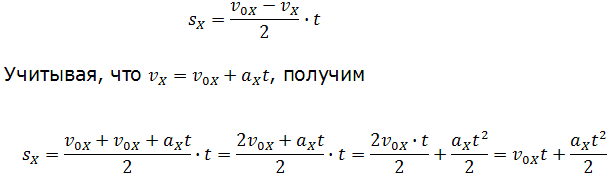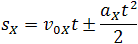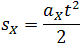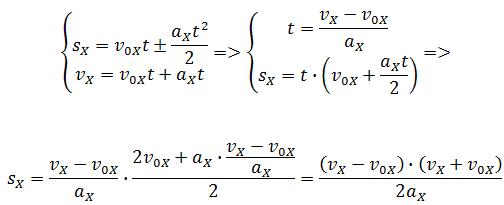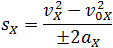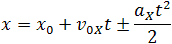Кинематические уравнения равнопеременного движения.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
= 
‘
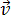
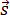
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
= ‘ = «
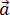
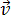
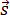
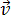
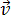
Учитывая, что 0 – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
Отсюда формула скорости равнопеременного движения в любой момент времени:
= 0 + t
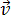
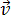
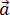
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
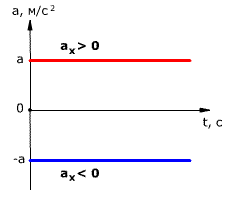
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
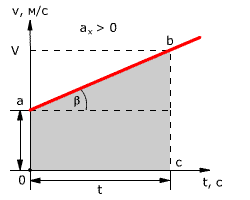
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
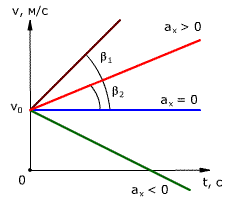
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
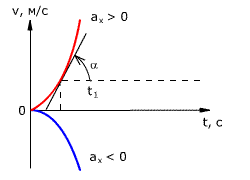
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратовпоможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, тоуравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
| | | следующая лекция ==> |
| | | Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. |
Дата добавления: 2016-01-29 ; просмотров: 7490 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Положение материальной точки в пространстве задается радиус-вектором
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
1. МЕХАНИКА
1.1. Кинематика
1.1.1. Краткие теоретические сведения
П
оложение материальной точки в пространстве задается
радиус-вектором 
,
где 
– единичные векторы направлений (орты);
x, y, z – координаты точки (рис. 1.1.1).
Абсолютное значение радиус-вектора 
.
Кинематические уравнения движения :
(в векторной форме) 
или (в координатной форме) 
, где t – время.
Уравнение траектории 
может быть получено из кинематических уравнений координат исключением времени.
Средняя скорость 
, где 
– перемещение материальной точки за время t .
Средняя скалярная (путевая) скорость: 
, где 
– путь, пройденный точкой за время 
.
Мгновенная скорость , 
,
где 
– проекции скорости на оси координат.
Абсолютное значение скорости 
.
Ускорение 
,
где 
– проекции ускорения на оси координат.
Абсолютное значение ускорения 
.
П
ри криволинейном движении ускорение можно представить как сумму нормальной 
и тангенциальной 
составляющей
. Абсолютное значение этих ускорений: 
,
где R – радиус кривизны в данной точке траектории.
Путь 
где 
– модуль скорости; 
и 
– начальный и конечный моменты времени, соответствующие пройденному пути.
Перемещение 
,
где 
– векторы, соответствующие начальному и конечному положениям материальной точки.
Кинематические уравнения равнопеременного движения (
)
,
где 
– начальная скорость.
Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) . Кинематическое уравнение вращательного движения = f ( t ).
Средняя угловая скорость = / t ,
где – изменение угла поворота за интервал времени t . Мгновенная угловая скорость 
.
Угловое ускорение 
.
Кинематические уравнения равнопеременного вращения ( = const ) 
,
где 0 – начальная угловая скорость.
Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами (рис. 1.1.3 и 1.1.4):
.
Рис. 1.1.3 Рис. 1.1.4
.1.2. Методические указания
В кинематике следует различать прямую и обратную задачи. В прямой задаче необходимо получить закон движения, если известны скорость, либо ускорение. В этих случаях используют формулы п. 1.1.1, предварительно проанализировав условие задачи. При анализе необходимо установить начальные условия и записать их в форме дополнительных уравнений. Начальные условия служат для определения констант интегрирования скорости или ускорения.
Систему координат необходимо выбирать в зависимости от условий задачи, чтобы математическое решение было упрощено. Во многих случаях этому требованию удовлетворяет декартова система координат.
Следует обратить внимание на то, что законы движения в координатной форме содержат не путь, проходимый движущимся телом, а только его координаты.
В обратных задачах задается закон движения, из которого скорость и ускорение находятся простым дифференцированием.
Как правило, закон движения удобно записывать либо в координатной форме, либо в векторной как изменение радиус-вектора материальной точки или центра масс системы в зависимости от координат и времени.
1.2. Динамика
1.2.1. Краткие теоретические сведения
Уравнение движения материальной точки (второй закон Ньютона)
в векторной форме 
, или при m = const , 
,
где 
– векторная сумма внешних сил, действующих на материальную точку; m – масса; 
– ускорение;
– импульс; N – число внешних сил действующих на точку.
В координатной форме (скалярной): 
, 
, 
,
где под знаком суммы стоят проекции сил 
на соответствующие оси координат.
C ила упругости 
,
где – 
коэффициент упругости (жесткость в случае пружины); x – абсолютная деформация.
Сила гравитационного взаимодействия 
,
где G – гравитационная постоянная;
и 
– массы взаимодействующих тел, рассматриваемых как материальные точки;
– расстояние между ними.
Сила трения скольжения 
,
где – коэффициент трения скольжения; N – сила нормальной реакции.
1.2.2. Методические указания
При решение задач данного раздела используются законы Ньютона. При этом особое внимание надо уделять анализу сил, действующих на рассматриваемое тело. Он должен включать: происхождение сил – в результате взаимодействия с каким телом возникла данная сила; природу сил – тяготение, упругость, трение; характер – от каких величин и как зависит данная сила.
Уравнение второго закона Ньютона следует записывать в векторной форме, а затем проецировать его на оси системы координат, выбранной в зависимости от условий задачи.
Законы Ньютона справедливы только для инерциальных систем отсчета. Почти во всех рассматриваемых задачах систему отсчета, связанную с Землей, можно считать инерциальной, если пренебрегать ее ускорением относительно системы неподвижных звезд. Отсюда вытекает ограничение в выборе системы отсчета: она не должна иметь ускорения относительно Земли.
При описании движения тел, связанных между собой, второй закон Ньютона целесообразно применять к каждому телу в отдельности, установив предварительно связь между координатами и кинематическими параметрами этих тел. При этом часто приходится накладывать дополнительные условия на характер связей.
1.3. Законы сохранения
1.3.1. Краткие теоретические сведения
1. Координаты центра масс системы материальных точек
; 
; 
,
где m – масса i — ой материальной точки; 
, 
, 
– ее координаты.
2. Закон сохранения импульса выполняется в замкнутой системе и записывается в виде: 
, где N – число материальных точек (или тел), входящих в систему.
3. Работа, совершаемая постоянной силой : 
,
где – угол между направлениями векторов силы 
и перемещения 
.
4. Мощность: 
, где 
– работа, совершаемая за промежуток времени 
.
5. Кинетическая энергия материальной точки (или тела, движущегося поступательно): 
.
6. Потенциальная энергия упруго деформированного тела (сжатой или растянутой пружины): 
, где – жесткость пружины, х – величина деформации.
7. Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m 1 и m 2 , находящихся на расстоянии r друг от друга: 
.
8. Потенциальная энергия тела, находящегося в однородном поле силы тяжести : 
, где h – высота тела над уровнем, принятым за начало отсчета потенциальной энергии.
9. Закон сохранения энергии в механик е выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде: 
.
1.3.2. Методические указания
Используя законы сохранения (импульса, энергии), можно найти связь между параметрами движения тела (координатами, скоростями) или системы тел в различных состояниях. В некоторых случаях, когда характер сил взаимодействия (закон изменения силы со временем, время взаимодействия) неизвестен, только законы сохранения позволяют найти по известным параметрам (координаты, скорости) системы в одном состоянии ее параметры в другом состоянии. Подобная ситуация, в частности, имеет место при кратковременных взаимодействиях, таких как удар, взрыв и т. п.
Решение задачи необходимо начинать с анализа сил, действующих на каждое тело системы. Такой анализ должен показать, целесообразно ли рассматривать каждое тело в отдельности либо систему тел; возможно ли к выбранной системе применять тот или иной закон сохранения.
Закон сохранения импульса можно применять, строго говоря, только к замкнутым системам, т. е. к системам тел, на которые не действуют внешние силы (либо векторная сумма внешних сил равна нулю). Природа внутренних сил не является существенной, к числу этих сил могут, например, относиться и силы трения.
При составлении уравнений на основании закона сохранения импульса следует обращать внимание на то, что скорости всех рассматриваемых тел должны определяться относительно одной и той же системы отсчета, а также на векторный характер закона.
Использование закона сохранения полной механической энергии предполагает консервативность рассматриваемой системы. И это условие обязательно необходимо проверять.
Если энергия системы включает потенциальную энергию тел во внешнем консервативном поле, то можно говорить о законе сохранения энергии одного тела, находящегося во внешнем консервативном поле, в частности, в поле тяжести Земли. Подобное рассмотрение предполагает, что расчеты производятся в системе отсчета, связанной со вторым телом, в данном случае с Землей.
При определении изменения энергии следует обращать внимание на то, что изменение потенциальной энергии тела во внешнем консервативном поле равно работе сил поля, взятой с обратным знаком. Сама потенциальная энергия не может быть вычислена без предварительного выбора начала отсчета потенциальной энергии.
1.6. Элементы механики жидкостей
1.6.1. Краткие теоретические сведения и методические
указания к решению задач
Используется единый подход к изучению жидкостей и газов, т. к. в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому пользуются единым термином «жидкость».
1. Давление жидкости – скалярная физическая величина, определяемая нормальной поверхностной силой, действующей со стороны жидкости на единицу площади:
, 
, 
, Па = Н/м 2 .
2. Закон Паскаля : жидкость (или газ) передает производимое на нее поверхностными силами внешнее давление по всем направлениям без изменения.
3 . Закон Архимеда : на тело, погруженное в жидкость (газ), действует со стороны жидкости направленная вверх сила, равная весу жидкости, объем которой совпадает с объемом погруженной в жидкость части тела:
, 
,
где – плотность жидкости, V – объем погруженной в жидкость части тела.
Жидкость, плотность которой с изменением давления не изменяется, называется несжимаемой.
4. Давление в жидкости .
– давление на свободной поверхности жидкости, часто оно равно атмосферному.
В точке А , погруженной в жидкость на высоту h , давление равно р (рис. 1.6.1) 
,
где 
– гидростатическое давление.
6. Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости:
,
где 
– полное давление, р – статическое давление, – гидростатическое давление, 
– динамическое давление.
7. Идеальная жидкость – физическая абстракция – жидкость, в которой отсутствуют силы внутреннего трения.
Формула Торричелли , определяющая скорость истечения идеальной жидкости через малое отверстие в открытом широком сосуде:
,
где h – глубина, на которой находится отверстие относительно свободной поверхности жидкости в сосуде.
Контрольное задание состоит из двух частей:
1 часть – задания открытого типа, необходимо не только выбрать единственный правильный ответ, но и дать пояснение к его решению.
2 часть – задания закрытого типа, необходимо представить подробное решение.
1.1. Физическая теория объяснила все известные в данной области физики явления и предсказала существование новых, неизвестных ранее явлений. Каким образом эта теория может быть опровергнута?
1. Созданием новой теории, предсказывающей другие неизвестные явления.
2. Теория будет опровергнута, если при проведении эксперимента предсказанные ею новые явления не будут обнаружены.
А. Только 1. Б . Только 2. В . Или 1, или 2. Г . Ни 1,ни 2. Д . Такая теория не может быть опровергнута.
1.2. На горизонтально движущуюся ленту транспортера соскальзывают кирпичи. Скорость ленты транспортера относительно Земли 
, скорость кирпича 
векторы и направлены параллельно. Через какой промежуток времени 
кирпич станет неподвижным относительно ленты, если коэффициент трения кирпича о ленту равен 
?
А . 
Б. 
В . 
Г . 
Д. 
1.3. Цилиндрический сосуд высотой 40 см заполнен водой. В боковой стенке сосуда есть три отверстия. Первое отверстие находится на расстоянии 10 см, второе — на расстоянии 20 см и третье — на расстоянии 30 см от основания сосуда. Если сосуд заполнен водой до верха, то из какого отверстия струя достигнет поверхности, на которой стоит сосуд, в наибольшем удалении от стенки сосуда?
А . Из первого. Б. Из второго. В. Из третьего. Г . Из первого и третьего. Д. Из всех трех одинаково.
1.4. В какую фазу Луны приливы в земных океанах и морях достигают максимального значения?
А. Только в полнолуние. Б. Только в новолуние. В . В полнолуние и новолуние. Г . В первую и последнюю четверть. Д. Высота прилива не зависит от фаз Луны.
1.5. Какую примерно силу нужно приложить к малому поршню гидравлического подъемника для подъема автомобиля массой 1000 кг, если площадь малого поршня 10 см 2 , площадь большого поршня 0,1 м 2 ?
А. 100 кг. Б. 10 кг. В . 1000 Н. Г . 100 Н. Д. 10 6 Н.
Кинематика
|
|
