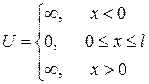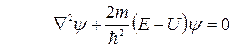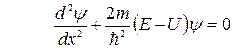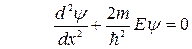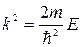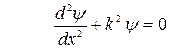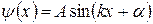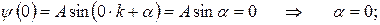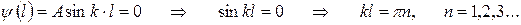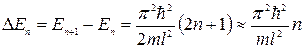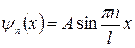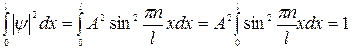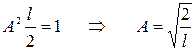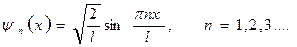Напишите решения уравнения шредингера для потенциальной ступени

Уравнение Шредингера для частицы в потенциальной яме.

Пусть частица движется вдоль оси X. При этом движение ограничено отрезком (0,l). В точках x=0 и x=l установлены непроницаемые бесконечно высокие стенки. Потенциальная энергия в этом случае имеет вид

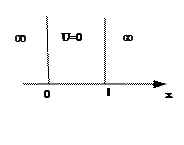
Такая зависимость потенциальной энергии от x получила название потенциальной ямы.

Запишем стационарное уравнение Шредингера

Поскольку пси-функция зависит только от координаты x, то уравнение упрощается следующим образом

Внутри потенциальной ямы U=0

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и пси-функция за пределами ямы равна нулю. Из условия непрерывности следует, что ψ должна быть равна нулю и на границах ямы, т.е. 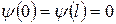. Это граничное условие, которому должны удовлетворять решения уравнения.

и получим уравнение, хорошо известное из теории колебаний

Решение такого уравнения имеет вид гармонической функции

Выбор соответствующих параметров k и α определяется граничными условиями, а именно,

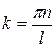
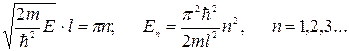
n = 0 отпадает, т.к. в этом случае ψ = 0 и частица нигде не находится. Следовательно, число k принимает лишь определенные дискретные значения, удовлетворяющие условию . Отсюда следует очень важный результат. Найдем собственные значения энергии частиц

,

т.е. энергия электрона в потенциальной яме не произвольна, а принимает дискретные значения, т.е. является квантованной. Величина Е_n зависит от целого числа n, которое принимает значение от 1 до ∞ и носит название главного квантового числа. Квантованные значения энергии называются энергетическими уровнями,а квантовое число n определяет номер энергетического уровня. Таким образом, электрон в потенциальной яме может находиться на определенном энергетическом уровне E_n. Причем минимальное значение энергии, соответствующее первому энергетическому уровню, отлично от нуля

.

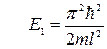
Определим расстояние между соседними энергетическими уровнями

При больших m и l расстояние между уровнями становится мало, и спектр становится квазинепрерывным. Относительное расстояние между уровнями

при n → ∞ ,

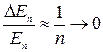
т. е. спектр становится непрерывен. В этом заключается принцип соответствия Бора: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.

Вернемся к задаче определения собственных функций. После применения граничных условий имеем

Для нахождения коэффициента А воспользуемся условием нормировки

Значение интеграла равно l /2.

Таким образом, собственные функции имеют вид

Графики собственных функций имеют вид

Окончательно сформулируем основные выводы:

1. Энергетический спектр частицы в потенциальной яме дискретный – энергия квантуется.

2. Минимальное значение кинетической энергии не может быть равно нулю.

3. Дискретный характер энергетических уровней проявляется при малых m, l и n , при больших m, l,n движение становится классическим.

4. Положения микрочастицы в яме не равновероятны, а определяются собственными функциями, в то время как в случае классической частицы все положения равновероятны.

Вопросы для самоконтроля:

1. Как определить вероятность нахождения частицы в некоторой точке?

2. Что называется потенциальной ямой?

3. Каково значение уравнения Шредингера? Что позволяет найти уравнение Шредингера?

4. Какие условия накладываются на пси-функцию?

5. Каков физический смысл главного квантового числа?

6. Почему квантовая механика является статистической теорией?

7. В чем состоит принцип соответствия Бора?

Уравнение Шредингера

Благодаря толкованию волн, изложенному де Бройлем, и соотношению неопределенностей Гейзенберга можно придти к тому, каким должно быть уравнение движения в рамках теории квантовой механики. Это должно быть равенство, которое описывает движения микрочастиц в силовом поле и из которого были бы видны волновые свойства частиц, наблюдаемые экспериментально. Также оно должно являться уравнением по отношению к волновой функции, поскольку вероятность, с которой частица пребывает в некоторый момент времени в объеме d V в области с координатами x y z , описывается с помощью именно этой величины. Поскольку нужное уравнение иллюстрирует волновые свойства частиц, то он должно само быть волновым уравнением (точно так же, как и уравнение, описывающее электромагнитную волну).

История появление теории

В 1962 г. Шредингер сформулировал положение, позже названное основным уравнением в нерелятивистской квантовой механике, или волновым уравнением Шредингера.

Эрвин Шредингер ( 1887 — 1961 , Австрия) был одним из физиков-теоретиков, которые основали квантовую механику. Он является автором трудов по статистической физике, квантовой теории, биофизике, а также общей теории относительности. Сформулировал основы теории движения микрочастиц – волновой механики (волновая теория Шредингера), а также квантовой теории возмущений (похожий метод в квантовой механике). Лауреат Нобелевской премии.

Отличительной особенностью уравнения Шредингера является то, что оно постулируется, а не выводится. Его истинность подтверждена экспериментально, следовательно, оно может считаться законом природы.

В наиболее общем виде его записывают так:

— h 2 m ∇ 2 Ψ + U ( x , y , z , t ) Ψ = i h ∂ 2 Ψ ∂ t 2 .

Здесь m обозначает массу частицы, i 2 — мнимую единицу, ∇ – так называемый оператор Лапласа, равный ∇ 2 Ψ = ∂ 2 Ψ ∂ x 2 + ∂ 2 Ψ ∂ y 2 + ∂ 2 Ψ ∂ z 2 , Ψ – искомую волновую функцию, а выражение U ( x , y , z , t ) соответствует потенциальной энергии частицы в определенной точке силового поля.

Описание движения частицы в потенциальном поле

Если поле, в котором происходит движение частицы, является потенциальным, то функция U не будет иметь явно выраженной зависимости от времени, и ей можно придать смысл потенциальной энергии. Тогда решить уравнение Шредингера можно разделением на сомножители: один из них будет зависеть только от времени, а второй – только от координаты точки.

Ψ ( x , y , z , t ) = Ψ ( x , y , z ) e — i E h t .

Параметр E обозначает полную энергию частицы. Если поле стационарное, то значение E остается постоянным. Подставив это значение в выражение выше, мы можем убедиться в его справедливости. При этом у нас получится формула Шредингера для стационарных состояний:

— h 2 2 m ∇ 2 Ψ + U Ψ = E Ψ .

∇ 2 Ψ + 2 m h 2 ( E — U ) Ψ = 0 .

Также данное выражение может быть записано в следующем виде:

Преобразование уравнения выполнено с использованием оператора Гамильтона H ^ . Его можно найти, сложив значения операторов — h 2 2 m ∇ 2 + U = H ^ . Гамильтониан – это оператор потенциальной энергии E .

Квантовая механика использует различные операторы также и в качестве других переменных, особенно динамических. Существуют операторы импульса, момента импульса, координат и т.д.