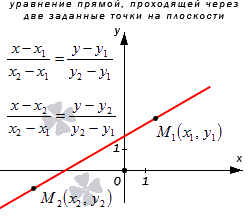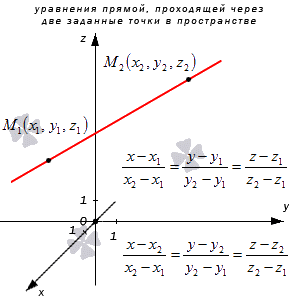Напишите уравнение данной прямой в прямоугольной системе координат

Выведите уравнение данной прямой в прямоугольной системе координат?

Геометрия | 5 — 9 классы

Выведите уравнение данной прямой в прямоугольной системе координат.

Через любые две точки можно провести только одну прямую.

Пусть известны координаты таких точек (в общем виде) А(х1 ; у1) и В(х2 ; у2)

Уравнение прямой, проходящей через эти две точки, можно вывести

(у — у1) / у2 — у1) = (х — х1)(х2 — х1).

Если прямая дана (построена на координатной прямой), выберем на ней две точки, координаты для которых без проблем можно определить, и подставим их в равенство, записанное выше.

Получим уравнение для данной прямой.

Прямая задана уравнением 2x — 3y + 6 = 0 a)начерите эту прямую б)запишите координаты точек пересечения прямой по осям координат?

Прямая задана уравнением 2x — 3y + 6 = 0 a)начерите эту прямую б)запишите координаты точек пересечения прямой по осям координат.

В) найдите площадь треугольника образованного осями координат и этой прямой.

Выведите формулу для вычисления расстояния между двумя точками по их координатам?

Выведите формулу для вычисления расстояния между двумя точками по их координатам.

1) Даны прямые : 3x — 2 ; y = 7, 5x — 5 ; y = 4x + 1?

1) Даны прямые : 3x — 2 ; y = 7, 5x — 5 ; y = 4x + 1.

На какой из этих прямых лежит точка с координатами : A(2 ; 4).

2) Cоставить уравнение параллельное ей прямой е1║е2 так, чтобы прямая е1 и e2 была с координатами : B(0 ; 8).

Поставьте уравнение прямой, проходящей через точки A ( — 1 ; — 2) и B (2 ; 10)?

Поставьте уравнение прямой, проходящей через точки A ( — 1 ; — 2) и B (2 ; 10).

Найдите координаты точки пересечения данной прямой с осью ординат.

Составьте уравнение прямой проходящей через точки A(2 ; — 3) и B(4 ; 1) ?

Составьте уравнение прямой проходящей через точки A(2 ; — 3) и B(4 ; 1) .

Найдите координаты точки пересечения данной прямой с осью абсцисс.

Дана окружность радиуса 10 с центром в начале координат а) запишите уравнение этой окружности б) найдите точки пересечения данной окружности с прямой y = 8?

Дана окружность радиуса 10 с центром в начале координат а) запишите уравнение этой окружности б) найдите точки пересечения данной окружности с прямой y = 8.

Дан прямоугольный параллелепипед со сторонами a 8 d 6 c 7 начало системы координат поместить в точку a указать направление всех координатных осей?

Дан прямоугольный параллелепипед со сторонами a 8 d 6 c 7 начало системы координат поместить в точку a указать направление всех координатных осей.

Постройте 5 точек в прямоугольной системе координат в пространстве?

Постройте 5 точек в прямоугольной системе координат в пространстве.

Выведите формулы выражающие координаты середины отрезка через координаты его концов?

Выведите формулы выражающие координаты середины отрезка через координаты его концов.

Даны координаты : А(4, — 4) В(6, 2) В( — 1, 8)Написать уравнение прямой CK, параллельной AB?

Даны координаты : А(4, — 4) В(6, 2) В( — 1, 8)

Написать уравнение прямой CK, параллельной AB.

На этой странице находится вопрос Выведите уравнение данной прямой в прямоугольной системе координат?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

На прямой р лежат (. ) А и Е. F, В и С лежат ниже прямой (или выше, это уж как нарисуешь, главное, чтобы в разных полуплоскостях с D), аD лежит выше прямой р (или ниже, опять всё зависит от того, где остальные точки).

∠EBK = ∠ECL ΔEBK = ΔECL по двум сторонам и углу, Значит ∠ ELC = ∠BKE = 110.

Нам даны точки : А(1 ; 3 ; 9), В( — 2 ; 4 ; 2) и С(3 ; 1 ; 0). Вектора и модули : АВ < - 2 - 1 ; 4 - 3 ; 2 - 0>или AB < - 3 ; 1 ; 2>. |AB| = √(9 + 1 + 4) = √14AC <3 - 1 ; 1 - 3 ; 0 - 0>или AC <2 ; - 2 ; 0>. |AC| = √(4 + 4 + 0) = √8. BC<3 + 2 ; 1 ..

Так как треугольник равнобедренный, то угол А равен углу С угол с образует смежный угол, сумма смежных углов равна 180, значит 180 — 125 = 55 это угол С(значит и А) сумма углов треугольника равна 180 градусов 55 + 55 = 110 180 — 110 = 70 угол В — 70 ..

70 градусов, угол В = 70.

Основание равнобедренного треугольника делится точкой касания вписанной окружности в отношении 1 : 1 = 5х : 5х отрезки касательных, проведенных из одной точки, равны, следовательно, часть боковой стороны, соответствующая цифре 5 равна половине основа..

8. ∠C = 180° — 123° = 57° (сумма смежных углов равна 180°) ∠А = ∠С (углы при основании равнобедренного треугольника) ⇒ ∠А = 57° Ответ : 57° 9. 30 % = 30 / 100 = 0, 3 30 % от 40 = 40 * 0, 3 = 12 (мин) Ответ : 12 минут.

1) длина вектора / а / = √(6² + 8²) = √100 = 10чтобы получить координаты ед. Вектора надо координаты a разделить на длину / a / ед. Вектор i<6 / 10 ; 8 / 10>i<0, 6 ; 0, 8>2) / b / = √(4 + 5) = √9 = 3j< - 2 / 3 ; 5 / 3>j< - 2 / 3 ; 1 2 / 3>.

Находим угол b. Так как ABCD РОМБ, то диагонали проходят под прямым углом, они равны и делят угол по полам значит угол bao равен 33 градусам. Сумма прямоугольного треугольника ABO равно 180 градусов значит угол ABO равен 180 — (90 + 33)равно 57. Т..

Уравнение прямой, которая проходит через две заданные точки: примеры, решения

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .

Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .

Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .

Рассмотрим подробней на решении нескольких примеров.

Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .

Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .

Ответ: x + 5 6 = y — 2 3 — 5 6 .

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .

Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .

Приведем каноническое уравнение к искомому виду, тогда получим:

x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0

Ответ: x — 3 y + 2 = 0 .

Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .

Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .

Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .

Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .

Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.

При подстановке получаем, что

— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3

Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .

Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .

Ответ: y = 2 3 x — 1 3 .

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .

Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .

Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .

По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:

x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5

Ответ: x — 2 — 1 = y + 3 0 = z — 5 .

58. Уравнения прямой в прямоугольной системе координат

Пусть в пространстве задана прямоугольная система координат OXy.

Определение 2. Нормальным вектором прямой A Называется любой ненулевой вектор N перпендикулярный Прямой а.

Пусть N = (A,B) ≠ 0, -нормальный вектор прямой а, M0(X0,Y0)- точка, принадлежащая прямой а. Пусть M(X,Y), произвольная точка пространства,

.

Тогда точка M принадлежит прямой а тогда и только тогда, когда векторы и N Ортогональны. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, Последнее в ортонормированном базисе можно записать в виде:

Таким образом, получаем уравнение прямой, Проходящей через точку M0(X0,Y0) и перпендикулярной вектору N = (A,B) ≠ 0.

Определение 3. Углом наклона прямой A Называется угол a, на который необходимо повернуть ось OX, чтобы ее направление совпало с направлением прямой а.

Определение 4. Угловым коэффициентом K прямой A, Не перпендикулярной оси OX,Называется тангенс угла наклона прямой а.

Пусть S = (M,L), — направляющий вектор прямой А, M0(X0,Y0)- точка, принадлежащая прямой А. Угол a наклона прямой А равен углу между вектором S и ортом оси OX. Если вектор S Не перпендикулярен оси OX, то M ≠ 0 и

Тогда из канонического уравнения (2) прямой находим

,

. (10)

Уравнение (10) называется уравнением прямой, Проходящей через точку M0(X0,Y0) с Угловым коэффициентом K.

Из (10) находим уравнение

Где B = Y0 — Kx0. Заметим, что B равно отрезку. отсекаемому прямой А на оси OX. Уравнение называется Уравнением прямой с угловым коэффициентом. Если на прямой А заданы две различные точки M1(X1,Y1), M2(X2,Y2) и X1 ≠ X2, то угловой коэффициент K Прямой А находится по формуле:

. (12)