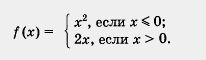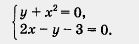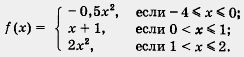Напишите уравнение параболы y = kx ^ 2 , график которой изображён на рисунке 10 и 12, помогите пжл?
Алгебра | 5 — 9 классы
Напишите уравнение параболы y = kx ^ 2 , график которой изображён на рисунке 10 и 12, помогите пжл.
Парабола проходит через точку с координатами (2 ; — 2)
Подставим в уравнение у = кх ^ 2
Х = 2 у = — 2 — 2 = к * 2 ^ 2 — 2 = 4к
График проходит через точку (1 ; 2)
График какой из перечисленных функций изображён на рисунке?
График какой из перечисленных функций изображён на рисунке?
График какой квадратичной функции изображён на рисунке?
График какой квадратичной функции изображён на рисунке?
Укажите график какого из указанных уравнений изображён на рисунке?
Укажите график какого из указанных уравнений изображён на рисунке.
Укажите график какого из указанных уравнений изображён на рисунке?
Укажите график какого из указанных уравнений изображён на рисунке.
Напиши уравнение параболы, изображённой на рисунке :Картинка приложенаДАМ 20 БАЛЛОВ?
Напиши уравнение параболы, изображённой на рисунке :
Помогите пожалуйста определить какой график функций изображён на рисунке)?
Помогите пожалуйста определить какой график функций изображён на рисунке).
Задайте формулой линейную функцию график которой изображён на рисунке?
Задайте формулой линейную функцию график которой изображён на рисунке.
На каком рисунке изображён график чётной функции?
На каком рисунке изображён график чётной функции?
На одном из рисунков изображён график функции у = 1 / х?
На одном из рисунков изображён график функции у = 1 / х.
Нарисуйте этот график.
Помогите пожалуйста?
Запиши формулу линейной функции, график которой изображён на рисунке :
Если вам необходимо получить ответ на вопрос Напишите уравнение параболы y = kx ^ 2 , график которой изображён на рисунке 10 и 12, помогите пжл?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Алгебра вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
Х ^ 3 + х ^ 2 — 4х — 4 = 0 х ^ 2(х + 1) — 4(х + 1) = 0 (х ^ 2 — 4)(х + 1) = 0 х ^ 2 — 4 = 0 или х + 1 = 0 (х — 2)(х + 2) = 0 или х = 0 — 1 х — 2 = 0 или х + 2 = 0 х = — 1 х = 0 + 2 х = 0 — 2 х = 2 х = — 2 Ответ : — 2 ; — 1 ; 2.
X ^ 3 + x ^ 2 — 4x — 4 = 0 x ^ 2 * (x + 1) — 4 * (x + 1) = 0 (x ^ 2 — 4) * (x + 1) = 0 (x — 2 )(x + 2)(x + 1) = 0 x = 2 x = — 2 x = — 1.
Y = arcCos(x + П / 4) y ‘ = — 1 / √(1 — (x + П / 4)²) Если задание y = arcCosx + П / 4, то y ‘ = (arcCosx) ‘ + (П / 4) ‘ = — 1 / √(1 — x²) + 0 = — 1 / √(1 — x²).
F(x) = arccosx + π / 4 f `(x) = (arccosx + π / 4)` = (arccosx)` + (π / 4)` = — 1 / √(1 — x²) + 0 = — 1 / √(1 — x²).
Х : — 240 ; — 120 : 300 ; 0, 12 У : — 0, 1 ; — 0, 2 ; 1, 6 ; 1 ;..
Функция у = kx2, ее свойства и график
Функция у = kx2, ее свойства и график
В 7-м классе мы изучали функции у = С, у = kx, у = kx + m, у = х 2 и пришли в итоге к выводу о том, что уравнение с двумя переменными вида у = f(x) (функция) есть математическая модель, удобная для того, чтобы, задав конкретное значение независимой переменной х (аргумента), вычислить соответствующее значение зависимой переменной у. Например, если дана функция у = х 2 , т.е. f(x) = х 2 , то при х = 1 получаем у = 1 2 = 1; короче это записывают так: f(1) = 1. При х = 2 получаем f(2)= 2 2 = 4, т. е. у = 4; при х = — 3 получаем f(- 3) = (- З) 2 = 9, т. е. у = 9, и т. д.
Уже в 7-м классе мы с вами начали понимать, что в равенстве у = f(х) правая часть, т.е. выражение f(x), не исчерпывается перечисленными выше четырьмя случаями (С, kx, kx + m, х 2 ).
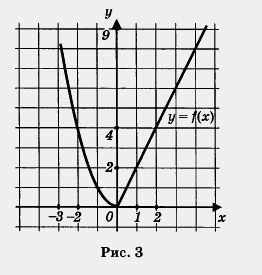
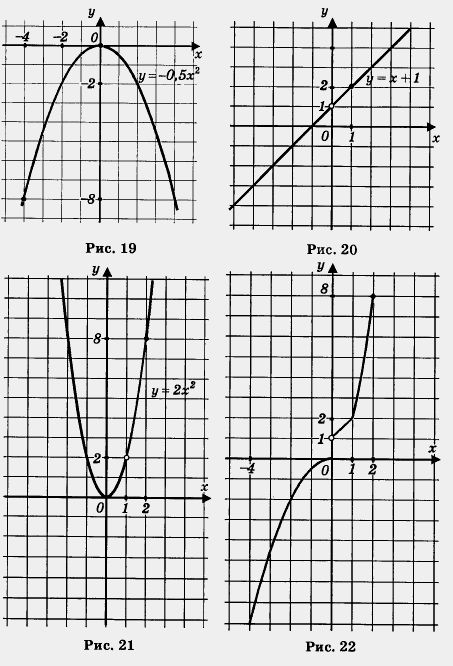
Так например, нам уже встречались кусочные функции, т. е. функции, заданные разными формулами на разных промежутках. Вот одна из таких функций:у = f(x), где
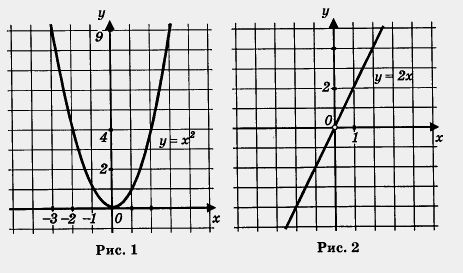
Помните, как строить графики таких функций? Сначала надо построить параболу у = х 2 и взять ее часть при х 0 (рис. 2). И, наконец, надо обе выделенные части объединить на одном рисунке, т. е. построить на одной координатной плоскости (см. рис. 3).
Теперь наша задача состоит в следующем: пополнить запас изученных функций. В реальной жизни встречаются процессы, описываемые различными математическими моделями вида у = f(x), не только теми, что мы перечислили выше. В этом параграфе мы рассмотрим функцию у = kx 2 , где коэффициент k — любое отличное от нуля число.
На самом деле функция у = kx 2 в одном случае вам немного знакома. Смотрите: если k = 1, то получаем у = х 2 ; эту функцию вы изучили в 7-м классе и, наверное, помните, что ее графиком является парабола (рис. 1). Обсудим, что происходит при других значениях коэффициента k.
Рассмотрим две функции: у = 2х 2 и у = 0,5x 2 . Составим таблицу значений для первой функции у = 2х 2 :
Построим точки (0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5) на координатной плоскости (рис. 4); они намечают некоторую линию, проведем ее (рис. 5).
Составим таблицу значений для второй функции у = 0,5x 2 :
Построим точки (0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), C; 4,5), (-3; 4,5) на координатной плоскости (рис. 6); они намечают некоторую линию, проведем ее (рис. 7)
Точки, изображенные на рис. 4 и 6, называют иногда контрольными точками для графика соответствующей функции.
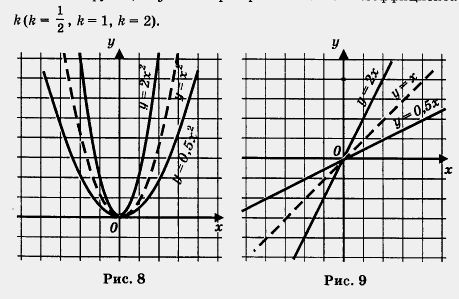
Сравните рисунки 1, 5 и 7. Не правда ли, проведенные линии похожи? Каждую из них называют параболой; при этом точку (0; 0) называют вершиной параболы, а ось у — осью симметрии параболы. От величины коэффициента k зависит «скорость устремления» ветвей параболы вверх или, как еще говорят, «степень крутизны» параболы. Это хорошо видно на рис. 8, где все три построенные выше параболы расположены на одной координатной плоскости.
Точно так же обстоит дело с любой другой функцией вида у = kx 2 , где k > 0. Графиком ее является парабола с вершиной в начале координат, ветви параболы направлены вверх, причем тем круче, чем больше коэффициент k. Ось у является осью симметрии параболы. Кстати, ради краткости речи математики часто вместо длинной фразы «парабола, служащая графиком функции у = kx 2 », говорят «парабола у = кх 2 », а вместо термина «ось симметрии параболы» используют термин «ось параболы».
Вы замечаете, что имеется аналогия с функцией у = kx? Если k > 0, то графиком функции у = kx является прямая, проходящая через начало координат (помните, мы говорили коротко:прямая у = kx), причем и здесь от величины коэффициента k зависит «степень крутизны» прямой. Это хорошо видно на рис. 9, где в одной системе координат изображены графики линейных функций у = kx при трех значениях коэффициента
Вернемся к функции у = kx 2 . Выясним, как обстоит дело в случае отрицательного коэффициента ft. Построим, например, график функции
у = — х 2 (здесь k = — 1). Составим таблицу значении:
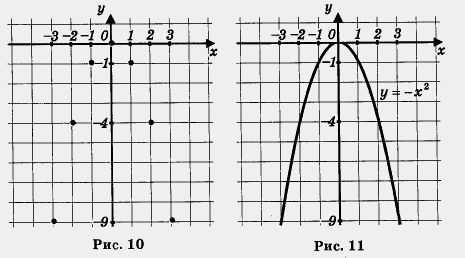
Отметим точки (0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; — 9) на координатной плоскости (рис. 10); они намечают некоторую линию, проведем ее (рис. 11). Это — парабола с вершиной в точке (0; 0), ось у — ось симметрии, но в отличие от случая, когда k > 0, на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента k.
Итак, графиком функции 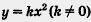
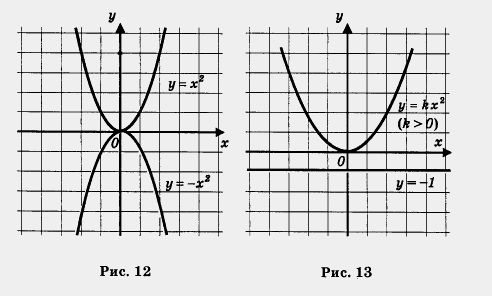
Если построить в одной системе координат графики функций у = х 2 и у = — х2, то нетрудно заметить, что эти параболы симметричны друг другу относительно оси х, что хорошо видно на рис. 12. Точно так же симметричны друг другу относительно оси х параболы у = 2х 2 и у = — 2х 2 (не поленитесь, постройте эти
две параболы в одной системе координат и убедитесь в справедливости сделанного утверждения).
Вообще, график функции у = — f(x) симметричен графику функции у = f(x) относительно оси абсцисс.
Свойства функции у = kx 2 при k > 0
Описывая свойства этой функции, мы будем опираться на ее геометрическую модель — параболу (рис. 13).
1. Так как для любого значения х по формуле у = kx 2 можно вычислить соответствующее значение у, то функция определена в любой точке х (при любом значении аргумента х). Короче это записывают так: область определения функции есть (-оо, +оо), т. е. вся координатная прямая.
2. у = 0 при х = 0; у > О при 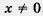
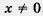
3. у = kx 2 — непрерывная функция. Напомним, что этот термин мы рассматриваем пока как синоним предложения «график функции есть сплошная линия, которую можно начертить, не отрывая карандаша от бумаги». В старших классах будет дано более точное математическое истолкование понятия непрерывности функции, не опирающееся на геометрическую иллюстрацию.
4.y/наим = 0 (достигается при х = 0); унаи6 не существует.
5. Функция у = kx 2 возрастает при х > О и убывает при х 2 расположен выше прямой у = — 1 (или у = — 2, это неважно) — она проведена на рис. 13. Значит, у — kx2 (k > 0) — ограниченная снизу функция.
Наряду с функциями, ограниченными снизу, рассматривают и функции, ограниченные сверху. Функцию у — f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа. Геометрически это означает, что график функции расположен ниже некоторой прямой, параллельной оси х.
Имеется ли такая прямая для параболы у = kx 2 , где k > 0? Нет. Это значит, что функция не является ограниченной сверху.
Итак, мы получили еще одно свойство, добавим его к тем пяти, что указаны выше.
6. Функция у = kx 2 (k > 0) ограничена снизу и не ограничена сверху.
Свойства функции у = kx 2 при k 2 — непрерывная функция.
4. унаи6 = 0 (достигается при х = 0), унаим не существует.
5. Функция возрастает при х 0.
6.Функция ограничена сверху и не ограничена снизу.
Дадим пояснения последнему свойству: имеется прямая, параллельная оси х (например, у = 1, она проведена на рис. 14), такая, что вся парабола лежит ниже этой прямой; это значит, что функция ограничена сверху. С другой стороны, нельзя провести такую прямую, параллельную оси х, чтобы вся парабола была расположена выше этой прямой; это значит, что функция не ограничена снизу.
Использованный выше порядок ходов при перечислении свойств функции не является законом, пока он сложился хронологически именно таким.
Более-менее определенный порядок ходов мы выработаем постепенно и унифицируем в курсе алгебры 9-го класса.
Пример 1. Найти наименьшее и наибольшее значения функции у = 2х 2 на отрезке: а) [0, 2]; б) [- 2, — 1]; в) [- 1, 1,5].
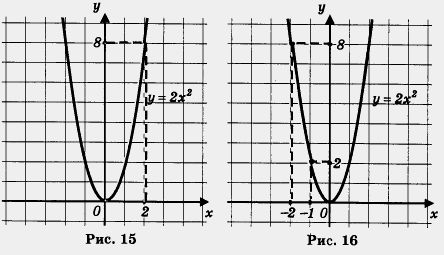
а) Построим график функции у = 2х 2 и выделим его часть на отрезке [0, 2] (рис. 15). Замечаем, что 1/наим. = 0 (достигается при х = 0), а унаиб = 8 (достигается при х = 2).
б) Построим график функции у = 2х 2 и выделим его часть на отрезке [- 2, — 1] (рис. 16). Замечаем, что 2/наим = 2 (достигается при х = — 1), а yнаиб = 8 (достигается при х = — 2).
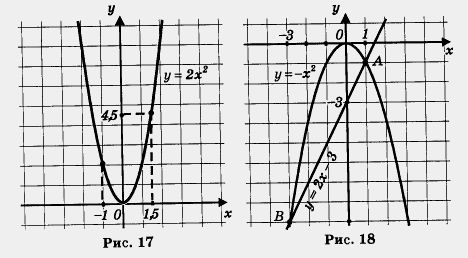
в) Построим график функции у = 2х 2 и выделим его часть на отрезке [- 1, 1,5] (рис. 17). Замечаем, что унанм = 0 (достигается при х = 0), а yнаиб достигается в точке х = 1,5; подсчитаем это значение:(1,5) = 2-1,5 2 = 2- 2,25 = 4,5. Итак, yнаиб =4,5.
Пример 2. Решить уравнение — х 2 = 2х — 3.
Решение. В учебнике «Алгебра—7» мы выработали алгоритм графического решения уравнений, напомним его.
Чтобы графически решить уравнение f(x) = g (x), нужно:
1) рассмотреть две функции у = -x 2 и у = 2x -3;
2) построить график функции i/ = / (х) ;
3) построить график функции у = g (x);
4) найти точки пересечения построенных графиков; абсцис-
сы этих точек — корни уравнения f(x) = g (x).
Применим этот алгоритм к заданному уравнению.
1) Рассмотрим две функции: у = — х2 и у = 2х — 3.
2) Построим параболу — график функции у = — х 2 (рис. 18).
3) Построим график функции у = 2х — 3. Это — прямая, для ее построения достаточно найти любые две точки графика. Если х = 0, то у = — 3; если х = 1,то у = -1. Итак, нашли две точки (0; -3) и (1; -1). Прямая, проходящая через эти две точки (график функции у = 2х — 3), изображена на том же чертеже (см. рис. 18).
4) По чертежу находим, что прямая и парабола пересекаются в двух точках А(1; -1) и Б(-3; -9). Значит, данное уравнение имеет два корня: 1 и — 3 — это абсциссы точек А и В.
Замечание. Разумеется, нельзя слепо доверять графическим иллюстрациям. Может быть, нам только кажется, что точка А имеет координаты (1; — 1), а на самом деле они другие, например (0,98; — 1,01)?
Поэтому всегда полезно проверить себя. Так, в рассмотренном примере надо убедиться, что точка А(1; —1) принадлежит параболе у = — х 2 (это легко — достаточно подставить в формулу у = — х 2 координаты точки А; получим — 1 = — 1 2 — верное числовое равенство) и прямой у = 2х — 3 (и это легко — достаточно подставить в формулу у = 2х — 3 координаты точки А; получим — 1 =2-3 — верное числовое равенство). То же самое надо сделать и для точки 8. Эта проверка показывает, что в рассмотренном уравнении графические наблюдения привели к верному результату.
Решение. Преобразуем первое уравнение системы к виду у = — х 2 . Графиком этой функции является парабола, изображенная на рис. 18.
Преобразуем второе уравнение системы к виду у = 2х — 3. Графиком этой функции является прямая, изображенная на рис. 18.
Парабола и прямая пересекаются в точках А(1; -1) и В (- 3; — 9). Координаты этих точек и служат решениями заданной системы уравнений.
Пример 4. Дана функция у — f (x), где
а) вычислить f(-4), f(-2), f(0), 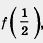
б) построить график функции;
в) с помощью графика перечислить свойства функции.
а) Значение х = — 4 удовлетворяет условию —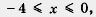
Значение 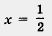
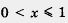
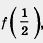
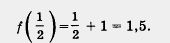
Аналогично получим f(2)= 2.2 2 =8.
Значение х = 3 не удовлетворяет ни одному из трех условий задания функции, а потому f(3) в данном случае вычислить нельзя, точка х = 3 не принадлежит области определения функции. Задание, состоящее в том, чтобы вычислить f(3), — некорректно.
б) Построение графика осуществим «по кусочкам». Сначала построим параболу у = -0,5x 2 и выделим ее часть на отрезке [-4, 0] (рис. 19). Затем построим прямую у = х + 1 и. выделим ее часть на полуинтервале (0, 1] (рис. 20). Далее построим параболу у = 2х 2 и выделим ее часть на полуинтервале(1, 2] (рис. 21).
Наконец, все три «кусочка» изобразим в одной системе координат; получим график функции у = f(x) (рис. 22).
в) Перечислим свойства функции или, как мы условились говорить, прочитаем график.
1. Область определения функции — отрезок [—4, 2].
2. у = 0 при х = 0; у > 0 при 0 2 . Найти:
f(1), f(- 2), f(а), f(2а), f(а + 1), f(-х), f(Зх),f(x — 1),
f(x + а), f(x) + 5, f(х) + b, f(x + а) + b, f(x 2 ), f(2х 3 ).
Решение. Так как f (х) = Зх 2 , то последовательно получаем:
f(1) =3.1 2 = 3;
f(a) = За 2 ;
f(а+1) = 3(а + 1) 2 ;
f(3х) = 3.(3х) 2 = 27х 2 ;
f(x + а) = 3(х + а) 2 ;
f( x 2 ) +b = 3x 2 +b
f(x 2 ) = 3. (x 2 ) 2 4
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Планирование математике, материалы по математике 8 класса скачать, учебники онлайн
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
http://edufuture.biz/index.php?title=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D1%83_=_kx2,_%D0%B5%D0%B5_%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0_%D0%B8_%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA