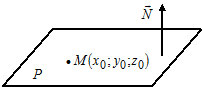Напишите уравнение прямой заданной точкой м0 х0

Уравнение прямой

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

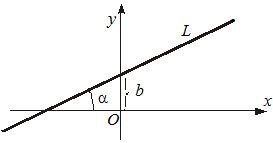
Общее уравнение прямой при B≠0 можно привести к виду

где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

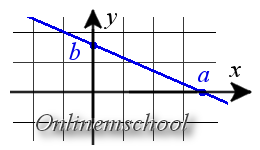
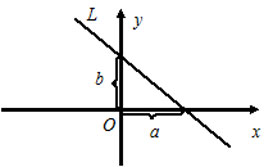
Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках

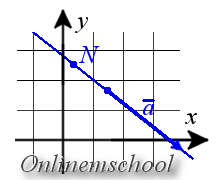
Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки M( x ₁, y ₁) и N( x ₂, y ₂), такие что x ₁ ≠ x ₂ и y ₁ ≠ y ₂, то уравнение прямой можно найти, используя следующую формулу

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x ₀ y = m t + y ₀

где N( x ₀, y ₀) — координаты точки лежащей на прямой, a = < l , m >— координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки N( x ₀, y ₀) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

x — 1 2 — 1 = y — 7 3 — 7

Упростив это уравнение получим каноническое уравнение прямой

Выразим y через x и получим уравнение прямой с угловым коэффициентом

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1 y = -4 t + 7

Решение. Так как M _y — N _y = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M( x ₁, y ₁, z ₁) и N( x ₂, y ₂, z ₂), такие что x ₁ ≠ x ₂, y ₁ ≠ y ₂ и z ₁ ≠ z ₂, то уравнение прямой можно найти используя следующую формулу

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x 0
	y = m t + y 0
	z = n t + z 0

где ( x ₀, y ₀, z ₀) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки M( x ₀, y ₀, z ₀) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач

В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.

Нормальное уравнение прямой – описание и пример

Рассмотрим выведение нормального уравнения.

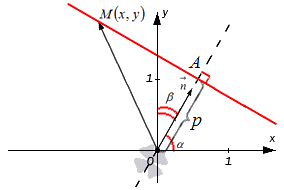
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.

Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .

O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .

Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p

Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y

Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.

Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.

Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.

Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .

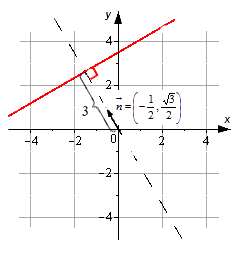
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .

Приведение общего уравнения прямой к нормальному виду

Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.

Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.

Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.

Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.

Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:

1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5

Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .

Нормальное уравнение по заданной прямой найдено.

Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Высшая математика.
• Аналитическая геометрия.

Аналитическая геометрия.

Прямая на плоскости, всевозможные уравнения.

Прямая на плоскости, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой:

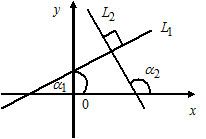
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$

2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $\alpha$ к оси $OX$ $(k=tg\alpha).$

3) $\frac=\frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

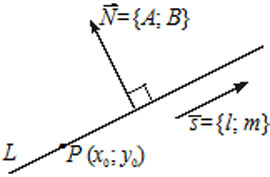
5) $\frac=\frac $ — каноническое уравнение прямой, где $\overline=(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(\overline\parallel L),$ точка $P(x_0, y_0)\in L.$

6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline=(A, B).$ Вектор $\overline N$ называется нормальным вектором прямой.

7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $\overline=(A, B) -$ нормальный вектор прямой $L.$

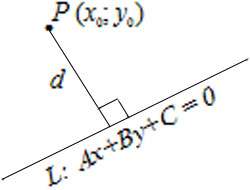
8) $x\cos\alpha+y\cos\beta-p=0 -$ нормальное уравнение прямой, где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac<\sqrt>\right|.$$

Расположение двух прямых на плоскости.

Условия параллельности двух прямых:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$

$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$

2) Пусть $L_1:$ $\frac=\frac,$ $\overline_1=(l_1, m_1);$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline_1\parallel\overline_2\Leftrightarrow$ $\frac=\frac.$

3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline_1\parallel\overline_2\Leftrightarrow$ $\frac=\frac.$

Условия перпендикулярности двух прямых:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$

$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$

$L_1\perp L_2\Leftrightarrow$ $k_1\cdot k_2=-1.$

2) Пусть $L_1:$ $\frac=\frac,$ $\overline_1=(l_1, m_1);$

$L_1\perp L_2\Leftrightarrow$ $\overline_1\perp\overline_2\Leftrightarrow$ $\cdot+\cdot=0.$

3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

$L_1\perp L_2\Leftrightarrow$ $\overline_1\perp\overline_2\Leftrightarrow$ $\cdot+\cdot=0.$

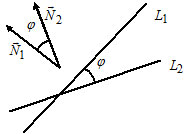
Угол между прямыми:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$

$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$

2) Пусть $L_1:$ $\frac=\frac,$ $\overline_1=(l_1, m_1);$

3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

Примеры:

2.141.

а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и нормальным вектором $\overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 6) для уравнения прямых ( $A(x-x_0)+B(y-y_0)=0$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=\overline N(2; 2):$

$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:

Нормальное уравнение прямой имеет вид $x\cos\alpha+y\cos\beta-p=0,$ где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Для нашей прямой имеем $A=1; B=1; C=-1 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac<-1><\sqrt<1+1>>=\frac<1><\sqrt 2>.$

Запишем нормальное уравнение прямой:

Расстояние от начала координат $p=\frac<1><\sqrt 2>.$

Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $\frac<1><\sqrt 2>x+\frac<1><\sqrt 2>y-\frac<1><\sqrt 2>=0;$ $p=\frac<1><\sqrt 2>.$

2.142.

а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и направляющим вектором $\overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 5) для уравнения прямых ( $\frac=\frac$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(l; m)=\overline S(3; -1):$ $\frac<3>=\frac<-1>$

Далее, приведем это уравнение к общему виду:

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Для нашей прямой имеем $A=1; B=3; C=-5 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac<-1><\sqrt<1+9>>=\frac<1><\sqrt<10>>.$

Запишем нормальное уравнение прямой:

Расстояние от начала координат $p=\frac<5><\sqrt <10>>.$

Ответ: $\frac<3>=\frac<-1>;$ общее уравнение $x+3y-5=0;$ нормальное уравнение прямой $\frac<1><\sqrt <10>>x+\frac<3><\sqrt <10>>y-\frac<5><\sqrt <10>>=0;$ $p=\frac<5><\sqrt <10>>.$

2.143.

а) Прямая $L$ задана двумя своими точками $M_1(1; 2)\in L$ и $M_2(-1; 0)\in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 3) для уравнения прямых ($\frac=\frac$ ) соответственно координаты точек $M_1(1; 2)= (x_1; y_1) $ и $M_2(-1; 0)=(x_2; y_2):$ $\frac<-1-1>=\frac<0-2>\Rightarrow \frac<-2>=\frac<-2>.$

Далее, приведем это уравнение к общему виду:

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Для нашей прямой имеем $A=1; B=-1; C=1 \Rightarrow sgn C=1.$ Таким образом, $\mu=-\frac<1><\sqrt<1+1>>=-\frac<1><\sqrt<2>>.$

Запишем нормальное уравнение прямой:

Расстояние от начала координат $p=\frac<1><\sqrt <2>>.$

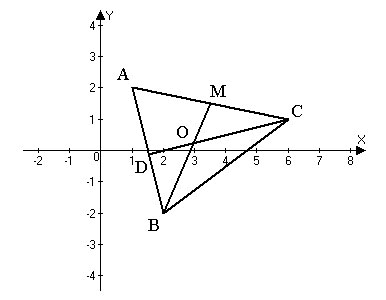
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:

1) Найти уравнение стороны $AB;$

2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$

3) найти угол между высотой $CD$ и медианой $BM.$

Решение.

1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $\frac=\frac. $

В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$

Подставляем координаты точек в уравнение прямой. Получаем $$\frac<2-1>=\frac<-2-2>\Rightarrow x-1=\frac<-4>.$$ Запишем общее уравнение прямой $AB$:

$-4(x-1)=y-2\Rightarrow$ $-4x+4=y-2\Rightarrow$ $4x+y-6=0.$

2) Уравнение прямой $CD$ найдем, пользуясь уравнением ( 6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline=(A, B).$

В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$

Таким образом, $$(x_0; y_0)=C=(6; 1);\quad\overline=\overline=(2-1; -2-2)=(1; -4).$$

Подставляем эти координаты в уравнение прямой:

$1(x-6)-4(y-1)=0\Rightarrow x-6-4y+4=0 \Rightarrow x-4y-2=0.$

То есть, уравнение прямой $CD:$ $x-4y-2=0.$

Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$

Решим систему методом исключений:

Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$

3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.

Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=\frac<2>; y_M=\frac<2>.$

Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой

$3.5(x-2)=1.5(y+2)\Rightarrow 3.5x-7=1.5y+3 \Rightarrow 3.5x-1.5y-10=0.$

Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле

где $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$

Ответ: 1) $AB: 4x+y-6=0.$

2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$

Решение.

Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$

Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$

Далее, чтобы найти координаты точки $B,$ решим систему уравнений:

$$\Rightarrow\left\<\beginx=y\\y=\frac<25><6>.\end\right.$$ Мы нашли координаты точки $B\left(\frac<25><6>, \frac<25><6>\right).$

Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $\left(\frac=\frac \right):$

$$\Rightarrow\frac<1>=\frac<7>\Rightarrow 7x-28=y-3\Rightarrow 7x-y-25=0.$$

Ответ: $7x-y-25=0.$

2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.

Решение:

Найдем уравнение диагонали $AC:$

Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $\overline=(1; -1).$ Прямая, перпендикулярная прямой $AC$ является параллельной нормальному вектору $\overline$. Таким образом, уравнение прямой $BD$ запишем по формуле 5) $\left(\frac=\frac\right),$ где $(x_0, y_0)=O(0; 2),$ $(l, m)=\overline=(1, -1):$

$$\frac<1>=\frac<-1>\Rightarrow x=-y+2 \Rightarrow x+y-2=0.$$

Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=\sqrt<(0-1)^2+(2-3)^2>=\sqrt<2>.$

Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$

Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой ( 3) — $\frac=\frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$

Деление отрезка в заданном отношении (векторный и координатный способы).

Деление отрезка в заданном отношении (векторный и координатный способы).

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

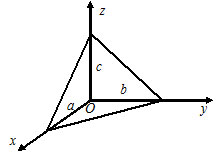
Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline,$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $\overline=r_1,$ $\overline=r_2,$ $\overline=r.$ Так как, $$\overline=r-r_1, \overline=r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac<1+\lambda>.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac<1+\lambda>, y=\frac<1+\lambda>, z=\frac<1+\lambda>.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac=\frac<1><2>;$$ $$x_C=\frac<1+\lambda_1>=\frac<3+\frac<1><2>\cdot 6><1+\frac<1><2>>=4;$$

Далее находим координаты точки $D:$

Ответ: $(4, 0)$ и $(5, 2).$

2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

Аналогичные равенства запишем для точки $D:$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$

Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения плоскости:

1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $\overline=(A, B, C) -$ нормальный вектор плоскости $P.$

2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline=(A, B, C).$ Вектор $\overline N$ называется нормальным вектором плоскости.

4) $\beginx-x_1&y-y_1&z-z_1\\x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&x_2-x_1&x_3-x_1\end=0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$

5) $x\cos\alpha+y\cos\beta+z\cos\gamma-p=0 -$ нормальное уравнение плоскости, где $\cos\alpha, \cos\beta$ и $\cos\gamma -$ направляющие косинусы нормального вектора $\overline,$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=\left|\frac<\sqrt>\right|.$$

Примеры:

2.180.

а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $\rho(P, P’).$

Решение.

Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $\overline=(-2, 1, -1).$

Далее запишем уравнение плоскости по формуле ( 2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline=(A, B, C).$

Ответ: $-2x+y-z+2=0.$

2.181.

а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$

Решение.

Из уравнения плоскости $P,$ находим ее нормальный вектор $\overline=(-1, 1, 0).$ Плоскость, перпендикулярная плоскости $P,$ параллельна ее нормальному вектору. Отсюда следует, что можно выбрать точку $M_3(x, y, z)\in P’$ такую, что что $\overline||\overline.$

Поскольку $z_N=0,$ то есть вектор $N\in XoY,$ то $z_=0.$

Мы нашли точку $M_3=(2, 1, 0).$

Так как точка $M_1\in P’,$ то и $M_3\in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$

$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0\Rightarrow$ $\Rightarrow-z+y-2+z+x-1=0\Rightarrow x+y-3=0.$

2.182.

а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$

Решение.

Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:

Таким образом $\overline=[a_1, a_2]=(1, -2, 1).$

Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $\overline N=(1, -2, 1):$

Ответ: $x-2y+z=0.$

2.183.

а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$

Решение.

Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $\overline,$ параллельного вектору $a,$ точка $M_3\in P.$

Пусть $M_3=(x, y, z).$ Тогда $\overline=(x-1, y-2, z).$ Так как $\overline||a,$ то $\frac>=\frac>=\frac>.$ $y_a=0,$ то есть вектор $a\in XoZ$ и всякий параллельный ему вектор так же будет принадлежать этой плоскости. Таким образом, $y_=y-2=0\Rightarrow y=2.$

Из условия параллельности векторов имеем $\frac<3>=\frac<1>.$ Пусть $x=4,$ тогда $z=1.$

Мы получили точку $M_3=(4, 2, 1).$

Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$

$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$

$\Rightarrow -x+1+3y-6+3z-y+2=0\Rightarrow -x+2y+3z-3=0.$

2.184.

а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$

Решение.

Воспользуемся формулой (4):

$\Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0\Rightarrow x+y-3=0.$