Научно-исследовательская работа на тему: «Уравнения высших степеней и способы их решения»
Скачать:
| Вложение | Размер |
|---|---|
| nauchno-issledovatelskaya_rabota_dodychenko_stepan.docx | 1.23 МБ |
| Краткое представление работы в виде слайдов | 1.59 МБ |
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
Подписи к слайдам:
Научно-исследовательская работа « Уравнения высших степеней и способы их решения » в ыполнил: Додыченко Степан у ченик 9 «Б» класса МБОУ Усть-Элегестинской СОШ р уководитель: Ильина Н.А., учитель математики
Актуальность выбранной темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением различных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать уравнения, что также пригодится и при решении более сложных задач, в том числе и при сдаче экзаменов.
Цель работы: изучить уравнения высшей степени и различные способы их решения. Задачи: рассмотреть стандартные и нестандартные методы решения уравнений высшей степени ; выявить наиболее удобные способы решения ; научиться решать уравнения высшей степени различными способами.
Объект исследования: уравнения высшей степени . Предмет исследования: способы решения уравнений высшей степени. Методы исследования: теоретические : изучение литературы по теме исследования, изучение тематических Интернет-ресурсов ; анализ полученной информации ; сравнение способов решения уравнений на удобство и рациональность.
Уравнения высшей степени и способы их решения Уравнение – это математическое выражение, являющееся равенством, содержащее неизвестное . Уравнение вида: называется уравнением n -ой степени .
Рассмотрим решения уравнений с одной переменной степени выше второй. Степенью уравнения Р(х) = 0 называется степень многочлена Р(х), т.е. наибольшая из степеней его членов с коэффициентом, не равным нулю. Так, например, уравнение (х 3 – 1) 2 + х 5 = х 6 – 2 имеет пятую степень, т.к. после операций раскрытия скобок и приведения подобных получим равносильное уравнение х 5 – 2х 3 + 3 = 0 пятой степени.
Способы решения уравнений высших степеней 1. Введение новой переменной Метод введения новой переменной заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = x n или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни: (t 1 , t 2 , …, t n ). После этого получают совокупность n уравнений q(x) = t 1 , q(x) = t 2 , … , q(x) = t n , из которых находят корни исходного уравнения.
Пример (х 2 + х + 1) 2 – 3х 2 — 3x – 1 = 0. Решение: (х 2 + х + 1) 2 – 3х 2 — 3x – 1 = 0. (х 2 + х + 1) 2 – 3(х 2 + x + 1) + 3 – 1 = 0. Замена (х 2 + х + 1) = t. t 2 – 3t + 2 = 0. t 1 = 2, t 2 = 1. Обратная замена: х 2 + х + 1 = 2 или х 2 + х + 1 = 1; х 2 + х — 1 = 0 или х 2 + х = 0; Из первого уравнения: х 1, 2 = (-1 ± √5)/2, из второго: 0 и -1.
Метод введения новой переменной находит применение при решении возвратных уравнений, то есть уравнений вида а 0 х n + а 1 х n – 1 + .. + а n – 1 х + а n =0, в котором коэффициенты членов уравнения, одинаково отстоящих от начала и конца, равны.
2. Разложение на множители методом группировки и формул сокращенного умножения
3. Разложение на множители методом неопределенных коэффициентов
4. Метод подбора корня по старшему и свободному коэффициенту
5. Графический метод. Данный метод состоит в построении графиков и использовании свойств функций. Решение:
– кубическая парабола сдвинута в вниз на 45 единиц -парабола ветвями в вниз, сдвинута по оси OX вправо на 0,9 единиц и по OY вверх 0,81 единиц
6.Умножение уравнения на функцию. Иногда решение алгебраического уравнения существенно облегчается, если умножить обе его части на некоторую функцию – многочлен от неизвестной. При этом надо помнить, что возможно появление лишних корней – корней многочлена, на который умножили уравнение.
Пример Решить уравнение: X 8 – X 6 + X 4 – X 2 + 1 = 0. (1) Решение: Умножив обе части уравнения на многочлен Х 2 + 1, не имеющий корней, получим уравнение: (Х 2 +1) (Х 8 – Х 6 + Х 4 – Х 2 + 1) = 0 (2) равносильное уравнению (1). Уравнение (2) можно записать в виде: Х 10 + 1= 0 (3) Ясно, что уравнение (3) не имеет действительных корней, поэтому уравнение (1) их не имеет. Ответ: нет решений.
Так же этим способом можно решать уравнения вида , где a ≠ 0, d ≠ 0, c ≠ a , a ( c — a ) = d ( b — d ). Тогда умножение этого уравнения на многочлен получим симметрическое уравнение четной степени, среди корней которого содержится и корень Отметим, что этот корень может быть посторонним корнем для уравнения.
Заключение Кроме названных методов решения уравнений высших степеней существуют и другие. Из общих методов решения уравнений высших степеней, которые встречаются чаще всего, используют: метод разложения левой части уравнения на множители; метод замены переменной (метод введения новой переменной); графический способ.
Научно-исследовательская работа по теме: « Уравнения высших степеней»
Практика олимпиад, выпускных и вступительных экзаменов по математике показывает, что довольно часто приходится сталкиваться с уравнениями высших степеней. Решение таких уравнений зачастую вызывает большие трудности. Не все уравнения удается решить. В школьных учебниках уравнение высшей степени – редкость. В данной работе представлены методы решения указанных уравнений.
Цели работы: Узнать какие методы решения высших степеней существуют; Научиться решать уравнения высших степеней различными способами.
Задачи:
1.Подобрать необходимую литературу
2.Отобрать материал для исследования, выбрать главную, интересную, понятную информацию
3.Проанализировать и систематизировать полученную информацию
4.Найти различные методы и приёмы решения уравнений высших степеней
5.Классифицировать исследуемые уравнения
6.Оформить работу в виде буклета
7.Создать электронную презентацию работы для представления собранного материала
Объект исследования: уравнения высших степеней
Просмотр содержимого документа
«Научно-исследовательская работа по теме: « Уравнения высших степеней»»
Муниципальное казенное общеобразовательное учреждение
«Богучарская средняя общеобразовательная школа № 1»
по теме: « Уравнения высших степеней»
Автор: Жуковская Татьяна Владимировна , 9 «Б» класс
Руководитель: Алабина Галина Юрьевна
Великие учёные, изучавшие уравнения высших степеней….……. 6
Виды уравнений высших степеней………………………………………. ….9
Методы решения высших степеней……………….………………..…………9
Решение уравнений разными способами..………………….……………. 10
Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Только в 11 веке таджикский поэт и ученый Омар Хаям впервые решил уравнение III степени. Установить, существует ли формула для нахождения корней любого уравнения, пытались многие. В конце 18 века французский ученый Луи Лагранж пытался доказать невозможность алгоритма общих уравнений, а вначале 19 века француз Галуа развил идею Лагранжа.
С тех пор математика пошла другим путем. Ученые стали искать другие методы решения уравнений высших степеней.
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Практика олимпиад, выпускных и вступительных экзаменов по математике показывает, что довольно часто приходится сталкиваться с уравнениями высших степеней. Решение таких уравнений зачастую вызывает большие трудности. Не все уравнения удается решить. В школьных учебниках уравнение высшей степени – редкость. Поэтому я выбрала эту тему для своей исследовательской работы.
Цели работы: Узнать какие методы решения высших степеней существуют; Научиться решать уравнения высших степеней различными способами.
1.Подобрать необходимую литературу
2.Отобрать материал для исследования, выбрать главную, интересную, понятную информацию
3.Проанализировать и систематизировать полученную информацию
4.Найти различные методы и приёмы решения уравнений высших степеней
5.Классифицировать исследуемые уравнения
6.Оформить работу в виде буклета
7.Создать электронную презентацию работы для представления собранного материала
Объект исследования: уравнения высших степеней
Методы исследования: изучение и анализ литературы, сравнение, обобщение, практический метод
Результат исследования: Я научилась решать возвратные и однородные уравнения,а также изучила теорему Безу и схему Горнера.
Гипотеза:Существует много различных видов и методов решения уравнений высших степеней, о которых не рассказывается в школьной программе 9 класса.
Великие учёные, изучавшие уравнения высших степеней
Омар Хайям (ок. 1048- ок. 1123)
Описал всевозможные виды уравнений третьей степени и рассмотрел сложные и красивые способы геометрических построений для отыскания их решения.
Никколо Тарталья (1499-1557)
Он вывел формулы для решения уравнений 3-ей степени, но своё открытие держал в тайне.
Обращался к Тарталье с просьбой сообщить ему формулу для решения кубических уравнений и обещал хранить её в секрете. Он не сдержал слово и опубликовал формулу, указав, что Тарталье принадлежит честь открытия «такого прекрасного и удивительного, превосходящего все таланты человеческого духа».
Нильс Хенрик Абель (1802-1829)
В 1826 году доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше.
Этьен Безу (1730-1783)
Французский математик, член Парижской академии наук. Преподавал математику в Училище гардемаринов в 1763 и Королевском артиллерийском корпусе в 1768. Основные его работы относятся к алгебре (исследование систем алгебраических уравнений высших степеней, исключение неизвестных в таких системах и др.) Является автором шеститомного «Курса математики» (1764-1769).
Уильям Джордж Горнер (1786 – 1837)
Английский математик. Основные труды по теории алгебраических уравнений. С его именем связана (1819) схема Горнера деления многочлена на двучлен .
Виды уравнений высших степеней
Уравнения третьей степени
Уравнения четвёртой степени
Уравнения пятой степени
Способы решения уравнений высших степеней
Разложение многочлена на множители:
По формулам сокращенного умножения
По теореме Безу
Метод введения новой переменной
Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена. Чтобы разложить многочлен на множители способом группировки, нужно: Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена. Вынести этот общий множитель за скобки.
Примеры решения уравнений способом группировки:
x-5=0 или x-4=0 или x+4=0
x-2=0 или x+2=0 или x-3=0
По формулам сокращенного умножения
1. Квадрат суммы: (a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности: (a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов: а 2 — b 2 = (a — b) (a + b)
4. Куб суммы: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Куб разности: (a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
6. Сумма кубов: a 3 + b 3 = (a + b) (a 2 — ab + b 2 )
7. Разность кубов: a 3 — b 3 = (a — b) (a 2 + ab + b 2 )
Примеры решения уравнений с помощью формул сокращённого умножения:
x=1 D=16-64=-48-корней нет
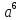
Научно — исследовательская работа по математике на тему «Различные способы решения квадратных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Муниципальное бюджетное общеобразовательное учреждение
средняя школа №12
городского округа город Выкса Нижегородской области
Различные способы решения квадратных уравнений
Естественно – научное отделение
Ученица 9 класса
Беспалова Галина Алексеевна
городской округ г. Выкса
Глава 1. Обзор литературы
1.1 История развития квадратных уравнений……………………………. 6
1.1.1 Квадратные уравнения в Древнем Вавилоне……………………………. 6
1.1.2 Как составлял и решал Диофант квадратные уравнения…………………6
1.1.3 Квадратные уравнения в Индии……………………………………………7
1.1.4 Квадратные уравнения ал- Хорезми ……………………………………. 8
1.1.5 Квадратные уравнения в Европе XIII — XVII в.в………………. 9
Глава 2. Материалы и методы исследования
Способы решения квадратных уравнений ………………………. 12
Разложение левой части уравнения на множители………………. 12
Метод выделения полного квадрата.……………………….……. 13
Решение квадратных уравнений по формулам …………………..…… 13
Решение уравнений с использованием теоремы Виета……………. 14
2.1.5 Решение уравнений способом «переброски»…………………………. 16
2.1.6 Свойства коэффициентов квадратного уравнения……………………. 17
2.1.7 Графическое решение квадратного уравнения……………………..…. 17
2.1.8 Решение квадратных уравнений с помощью циркуля и линейки……. 19
2.1.9 Решение квадратных уравнений с помощью номограммы…………….21
2.1.10 Геометрический способ решения квадратных уравнений……………..22
2.2. Исследование. Решение квадратных уравнений учащимися 9,11 классов……………………………………………………………………………23
Глава 3. Результаты и их обсуждения…………………………………………..24
Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Изучив решение квадратных уравнений, мне захотелось узнать, можно ли еще другими способами решить уравнение и в дальнейшем использовать различные способы при решении уравнений.
Цель работы : изучить способы решения квадратного уравнения, которые мы не изучаем на уроке. Научиться использовать эти способы.
Для достижения поставленной цели были намечены следующие задачи:
Изучить историю развития квадратных уравнений.
Найти информацию о способах решения квадратного уравнения.
Решить квадратное уравнение различными способами и выяснить, какой способ удобен для решения этого уравнения.
При решении сформулированных задач была изучена специальная литература, собрана информация статистических данных для последующего использования в работе, проведено исследование по решению квадратного уравнения учащимися 9 и 11 классов с целью выявления различных способов решения квадратного уравнения.
Результаты исследований показали, что учащиеся используют при решении квадратных уравнений методы, изученные по школьной программе.
Я считаю эту тему актуальной, т. к. она может пригодиться нам не только во время обучения в школе, а впоследствии и в ВУЗе, и на протяжении всей жизни.
Описание новизны и практической значимости : решение одного квадратного уравнения несколькими способами и выбор более рационального способа.
Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Теория уравнений в школьном курсе алгебры занимает ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Это связано с тем, что большинство жизненных задач сводится к решению различных видов уравнений.
В учебнике алгебры для 8 класса мы знакомились с несколькими видами квадратных уравнений, и отрабатывали их решение по формулам. У меня возник вопрос «Существуют ли другие способы решения квадратных уравнений? Насколько сложны данные способы и можно ли ими пользоваться на практике?» Поэтому я выбрала тему исследования, связанную с квадратными уравнениями, в ходе работы она получила название «Различные способы решения квадратных уравнений». Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, это также может мне пригодится при решении более сложных задач, в том числе и в 10-11 классах, и при сдаче ОГЭ и ЕГЭ.
Цель работы: изучить различные способы решения квадратных уравнений, научиться применять их при решении и выбрать наиболее рациональныйспособ решения.
Исходя из данной цели, мною были поставлены следующие задачи:
— изучить историю развития квадратных уравнений;
— рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
— выявить наиболее рациональные способы решения квадратных уравнений;
— научиться решать квадратные уравнения различными способами.
Объект исследования : квадратные уравнения.
Предмет исследования : способы решения квадратных уравнений.
Теоретические: изучение литературы по теме исследования;
Анализ: информации, полученной при изучении литературы; результатов полученных при решении квадратных уравнений различными способами.
Сравнение: способов на рациональность их использования при решении квадратных уравнений.
Гипотеза: существуют различные рациональные способы решения квадратных уравнений
Глава 1. Обзор литературы.
1.1 История развития квадратных уравнений .
1.1.1 Квадратные уравнения в Древнем Вавилоне .
Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
1.1.2 Квадратные уравнения в Греции или как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х , другое же меньше, т.е. 10 — х . Разность между ними 2х .
Отсюда х = 2 . Одно из искомых чисел равно 12 , другое 8 . Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
1.1.3 Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхатой. Другой индийский ученый, Брахмагупта ( VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах 2 + b х = с, а> 0.(1)
В уравнении (1) коэффициенты, кроме а , могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
« Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис.).
Соответствующее задаче уравнение:
Бхаскара пишет под видом: х 2 — 64х = -768
и, чтобы дополнить левую часть этого
уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем: х 2 — 64х + 32 2 = -768 + 1024,
1.1.4 Квадратные уравнения ал — Хорезми.
В алгебраическом трактате ал — Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах 2 + с = b х.
2) «Квадраты равны числу», т.е. ах 2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах 2 + с = b х.
5) «Квадраты и корни равны числу», т.е. ах 2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах 2 .
Для ал — Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с современным решением. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал — Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал — Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Задача . «Квадрат и число 21 равны 10 корням. Найти корень»
(подразумевается корень уравнения х 2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
1.1.5 Квадратные уравнения в Европе XIII — XVII в.в.
Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из
« Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII .
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду: х 2 + bx = с,
при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
1.1.6. О теореме Виета
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D , умноженное на A — A 2 , равно BD , то A равно В и равно D ».
Чтобы понять Виета, следует вспомнить, что А , как и всякая гласная буква, означало у него неизвестное (наше х ), гласные же В, D — коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
http://multiurok.ru/files/nauchno-issliedovatiel-skaia-rabota-po-tiemie-urav.html
http://infourok.ru/nauchno-issledovatelskaya-rabota-po-matematike-na-temu-razlichnie-sposobi-resheniya-kvadratnih-uravneniy-1358076.html







