Парабола: формулы, примеры решения задач
Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы имеет вид:

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.
На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
В математическом анализе принята другая запись уравнения параболы:
то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.
Фокус параболы имеет координаты
Директриса параболы определяется уравнением 
Расстояние r от любой точки 

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.
Пример 1. Определить координаты фокуса параболы
Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:
Находим координаты фокуса параболы:
Пример 2. Составить уравнение директрисы параболы
Решение. Находим p:
Получаем уравнение директрисы параболы:
Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.
Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:
Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.
Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
Парабола
Парабола, её форма, фокус и директриса.
Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^<2>=2px\label
$$
при условии \(p > 0\).
Из уравнения \eqref
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции \(y=ax^<2>\). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством \(2p=a^<-1>\).
Фокусом параболы называется точка \(F\) с координатами \((p/2, 0)\) в канонической системе координат.
Директрисой параболы называется прямая с уравнением \(x=-p/2\) в канонической системе координат (\(PQ\) на рис. 8.11).
Рис. 8.11. Парабола.
Свойства параболы.
Расстояние от точки \(M(x, y)\), лежащей на параболе, до фокуса равно
$$
r=x+\frac
<2>.\label
$$
Вычислим квадрат расстояния от точки \(M(x, y)\) до фокуса по координатам этих точек: \(r^<2>=(x-p/2)^<2>+y^<2>\) и подставим сюда \(y^<2>\) из канонического уравнения параболы. Мы получаем
$$
r^<2>=\left(x-\frac
<2>\right)^<2>+2px=\left(x+\frac
<2>\right)^<2>.\nonumber
$$
Отсюда в силу \(x \geq 0\) следует равенство \eqref
Заметим, что расстояние от точки \(M\) до директрисы также равно
$$
d=x+\frac
<2>.\nonumber
$$
Следовательно, мы можем сделать следующий вывод.
Для того чтобы точка \(M\) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.
Докажем достаточность. Пусть точка \(M(x, y)\) одинаково удалена от фокуса и от директрисы параболы:
$$
\sqrt<\left(x-\frac
<2>\right)^<2>+y^<2>>=x+\frac
<2>.\nonumber
$$
Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы \eqref
Параболе приписывается эксцентриситет \(\varepsilon=1\). В силу этого соглашения формула
$$
\frac
$$
верна и для эллипса, и для гиперболы, и для параболы.
Уравнение касательной к параболе.
Выведем уравнение касательной к параболе в точке \(M_<0>(x_<0>, y_<0>)\), лежащей на ней. Пусть \(y_ <0>\neq 0\). Через точку \(M_<0>\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt<2px>\) или же \(y=-\sqrt<2px>\), смотря по знаку \(y_<0>\).) Для функции \(f(x)\) выполнено тождество \((f(x))^<2>=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_<0>\) и \(f(x_<0>)=y_<0>\), находим \(f'(x_<0>)=p/y_<0>\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_<0>=\frac
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_<0>^<2>=2px_<0>\). Теперь уравнение касательной принимает окончательный вид
$$
yy_<0>=p(x+x_<0>).\label
$$
Заметим, что для вершины параболы, которую мы исключили, положив \(y_ <0>\neq 0\), уравнение \eqref
Касательная к параболе в точке \(M_<0>\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_<0>\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).
Рассмотрим касательную в точке \(M_<0>(x_<0>, y_<0>)\). Из уравнения \eqref
$$
(\overrightarrow
<2>y_<0>+py_<0>=y_<0>(x_<0>+\frac
<2>).\nonumber
$$
Но \(|\overrightarrow
Заметим, что \(|FN|=|FM_<0>|\) (см. рис. 8.12).
Задача 31453 Пожалуйста помогите 1)определить.
Условие
Пожалуйста помогите
1)определить величину параметра расположение относительно координатных оси следующих парабол: y^2=6x x^2=5y
2)найти фокус и уравнение директрисы параболы y^2=24x
Решение
Канонические уравнения параболы:
x^2=2py cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
Фокус F(0;p/2)
Уравнение директрисы:
y=-p/2
x^2=-2py cимметрична относительно оси Оу, ветви направлены в сторону противоположную оси Оу
Фокус F(0;-p/2)
Уравнение директрисы:
y= p/2
y^2=2px cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(p/2;0)
Уравнение директрисы:
x=-p/2
y^2=-2px cимметрична относительно оси Ох, ветви направлены в сторону противоположную оси Ох
Фокус F(-p/2;0)
Уравнение директрисы:
x=p/2
[b]Решение[/b]:
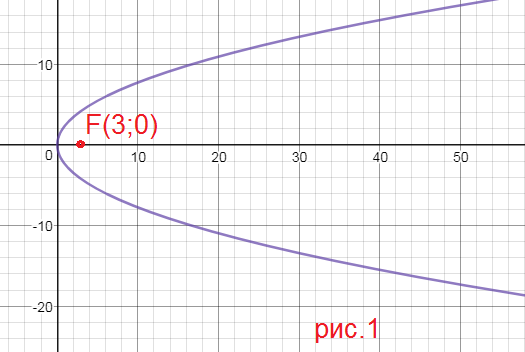
1) y^2=6x ⇒ 2p=6;
p=3
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
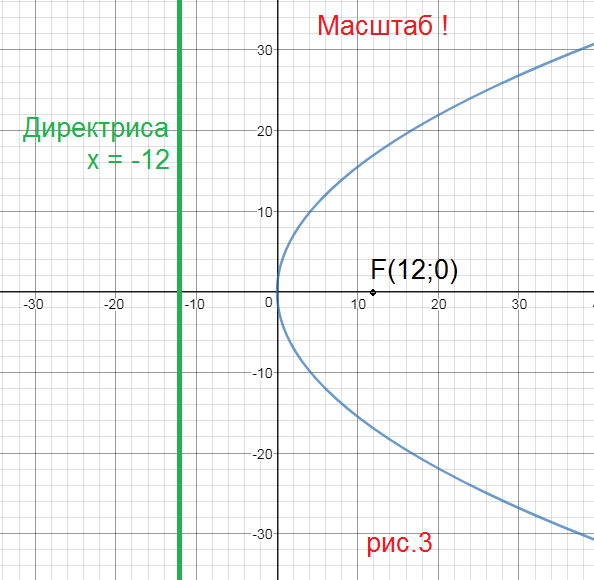
x^2=5y 2p=5 ⇒ 2p=5;
p=2,5
cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
2)
y^2=24x ⇒ 2p=24;
p=12
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(12;0)
Уравнение директрисы:
x=-12
см. рис.3 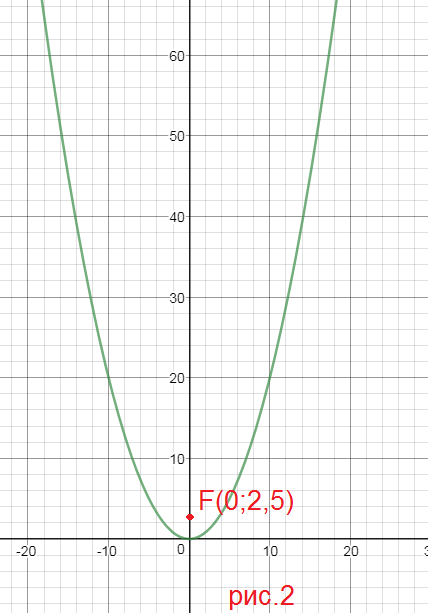
http://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/parabola/
http://reshimvse.com/zadacha.php?id=31453