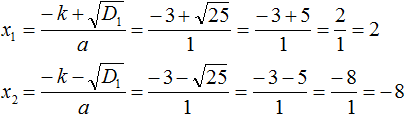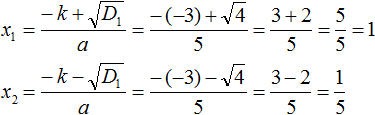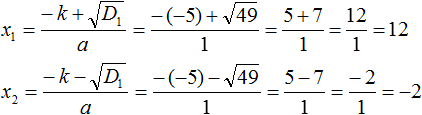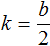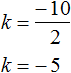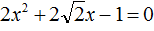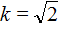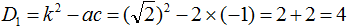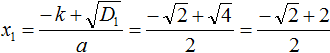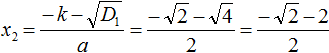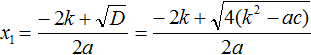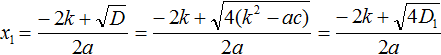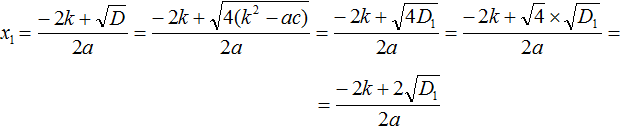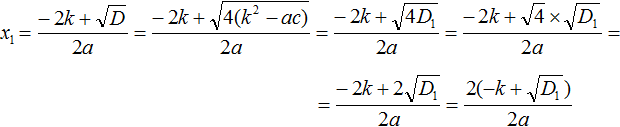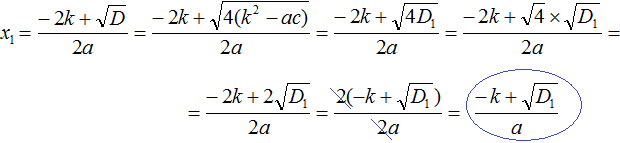Найдите коэффициент k для уравнения

Как найти k и b по графику линейной функции?

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти \(k\) и \(b\) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти \(k\) и \(b\), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось \(y\) в точке \(b\).
Примеры:

Но не советую определять так \(b\), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Если функция возрастает, то знак коэффициента \(k\) плюс, если убывает – минус, а если постоянна, то \(k=0\).

Чтоб конкретнее определить \(k\) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить \(k\) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

\(b=3\) – это сразу видно. Функция идет вниз, значит \(k 0\). \(k=+\frac=\frac<4><4>=1,b=1\). \(f(x)=x+1\).

Теперь перейдем к функции \(g(x)\). Найдем координаты точек \(D\) и \(E\): \(D(-2;4)\), \(E(-4;1)\). Можно составить систему:

Вычтем второе уравнение из первого, чтоб убрать \(b\):

\(g(x)=1,5x+7\). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем \(f(x)\) и \(g(x)\).

Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k 2 − ac , а корни по формулам и .

Примеры

Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .

Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .

Например, число 10 можно представить как 2 × 5 .

В этом произведении k = 5 .

Число 12 можно представить как 2 × 6 .

В этом произведении k = 6 .

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7 .

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .

В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k 2 − ac

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .

В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D₁ = k 2 − ac не нужно выполнять умножение числа 4 на ac .

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

Пример 5. Решить квадратное уравнение

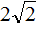
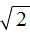
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что

Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .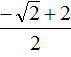

Вычислим второй корень уравнения:

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k

Теперь вычислим дискриминант по ранее известной формуле:

Вынесем в получившемся выражении за скобки общий множитель 4

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .

В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)

Но ранее было сказано, что выражение k 2 − ac обозначается через D₁ . Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Коэффициенты k и b

Содержание

Положение прямой на графике зависит от величины коэффициентов $k$ и $b$

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

При $k > 0$ угол между графиком и осью $Ox$ меньше $90 \degree$ (острый)

При $k

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат.

Другими словами, коэффициент $b$ показывает, насколько график сдвинут вдоль оси $Oy$. Если $b > 0$, то график будет сдвинут вверх, и если $b

Так на нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

График функции $y=50x + 500$

Частные случаи. b = 0

В случае, когда коэффициент $b = 0$, а функция прямо пропорциональна, ее график будет проходить через начало координат $O(0;0)$. Ведь при подставлении в формулу $x = 0$ получим и $y = 0$.

Для построения графика такой функции достаточно найти одну точку, вторая – начало координат $О(0;0)$.

Важно: график в виде вертикальной прямой, параллельной оси $Oy$, не является графиком функции. В таком случае одному значению аргумента соответствует множество значений $y$. Это не наш случай, потому что он не соответствует самому определению функции.

При этом прямой, параллельной оси $Ox$, график функции может быть. Это возможно, когда коэффициент $k = 0$. Угол наклона также будет равен $0$. Формула принимает вид $y = b$.