Упражнения
1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .
2. Нарисуйте кривую, задаваемую уравнением r = cos φ .
3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?
6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?
7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = 
8. Нарисуйте спираль Галилея , которая задается уравнением r = a 
9. Нарисуйте кривую, задаваемую уравнением r = | 
10. Нарисуйте кривую, задаваемую уравнением r = 
11. Нарисуйте кривую, задаваемую уравнением r = 
12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.
1. Березин В. Кардиоида //Квант. – 1977. № 12.
2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.
3. Берман Г.Н. Циклоида. – М.: Наука, 1975.
4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.
5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.
7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.
8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.
9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.
10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.
Точка пересечения прямых на плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых на плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический», «параметрический» или «общий»), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямых на плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в общем виде.
- 2. Точка пересечения прямых, заданных в каноническом виде.
- 3. Точка пересечения прямых, заданных в параметрическом виде.
- 4. Точка пересечения прямых, заданных в разных видах.
- 5. Примеры нахождения точки пересечения прямых на плоскости.
1. Точка пересечения прямых, заданных в общем виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (1) |
| L2: A2x+B2y+C2=0 | (2) |
Для нахождения точки пересечения прямых (1) и (2) нужно решить систему линейных уравнений (1) и (2) относительно переменных x,y. Для этого запишем систему (1),(2) в матричном виде:
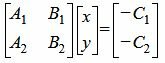 | (3) |
Построим расширенную матрицу:
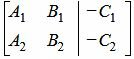 | (4) |
Приведем (4) к верхнему диагональному виду. Пусть A1≠0 . Тогда сложим строку 2 со строкой 1, умноженной на −A2/A1:
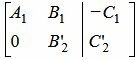 | (5) |
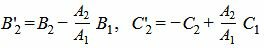 |
Если B’2=0 и С’2=0, то система линейных уравнений имеет множество решений. Следовательно прямые L1 и L2 совпадают. Если B’2=0 и С’2≠0, то система несовместна и, следовательно прямые параллельны и не имеют общей точки. Если же B’2≠0, то система линейных уравнений имеет единственное решение. Из второго уравнения находим y: y=С’2/B’2 и подставляя полученное значение в первое уравнение находим x: x=(−С1−B1y)/A1. Получили точку пересечения прямых L1 и L2: M(x, y).
Подробнее о решении систем линейных уравнений посмотрите на странице метод Гаусса онлайн.
2. Точка пересечения прямых, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
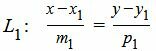 | (6) |
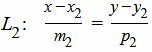 | (7) |
Приведем уравнение L1 к общему виду. Сделаем перекрестное умножение в уравнении (6):
| p1(x−x1)=m1(y−y1) |
Откроем скобки и сделаем преобразования:
| p1x−m1y−p1x1+m1y1=0 |
| A1x+B1y+C1=0 | (8) |
Аналогичным методом получим общее уравнение прямой (7):
| A2x+B2y+C2=0 | (9) |
Терерь можно найти точку пересечения прямых L1 и L2 методом, описанным в параграфе 1.
3. Точка пересечения прямых, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
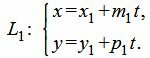 | (10) |
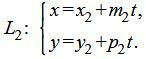 | (11) |
Приведем уравнение прямой L1 к каноническому виду. Для этого из уравнений (10) найдем параметр t:
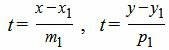 | (12) |
Из уравнений (12) следует:
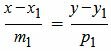 |
Аналогичным образом можно найти каноническое уравнение прямой L2:
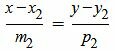 |
Как найти точку пересечения прямых, заданных в каноническом виде описано выше.
4. Точка пересечения прямых, заданных в разных видах.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (13) |
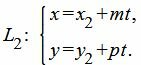 | (14) |
| A1(x2+mt)+B1(y2+pt)+C1=0, | (15) |
| A1x2+A1mt+B1y2+B1pt+C1=0, |
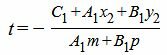 | (16) |
Если числитель и знаменатель в (16) одновременно равны нулю, то любое значение t удовлетворяет уравнению (15), следовательно прямые L1 и L2 совпадают. Если знаменатель равен нулю а числитель отличен от нуля, то прямые L1 и L2 не пересекаются, т.е. они параллельны.
Пусть знаменатель не равен нулю. Подставляя полученное значение t в (14), получим координаты точки пересечения прямых L1 и L2.
5. Примеры нахождения точки пересечения прямых на плоскости.
Пример 1. Найти точку пересечения прямых L1 и L2:
| L1: 2x+y+4=0, | (17) |
| L2: x−3y+2=0. | (18) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (17) и (18). Представим уравнения в матричном виде:
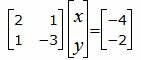 | (19) |
Решим систему линейных уравнений отностительно x, y. Для этого воспользуемся методом Гаусса. Получим:
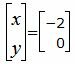 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
| L1: 2x+3y+4=0, | (20) |
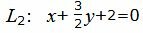 | (21) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (20) и (21). Представим уравнения в матричном виде:
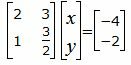 | (22) |
Для решения (22) воспользуемся методом Гаусса. Получим:
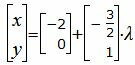 |
где λ− произвольное действительное число.
Имеем больше одного решения. Это означает, что прямые L1 и L2 совпадают.
Пример 3. Найти точку пересечения прямых L1 и L2:
| L1: −5x+y+9=0, | (23) |
| L2: −10x+2y−3=0, | (24) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (23) и (24). Представим уравнения в матричном виде:
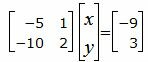 | (25) |
Применив метод Гаусса получим, что система (25) несовместна. Следовательно эти прямые не пересекаются, т.е. они параллельны.
Ответ. Прямые L1 и L2 не имеют общую точку, т.е. они параллельны.
Пример 4. Найти точку пересечения прямых L1 и L2:
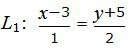 | (26) |
| L2: x+2y−9=0, | (27) |
Приведем, сначала, уравнение прямой (26) к общему виду:
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (28) и (27). Представим уравнения в матричном виде:
 | (29) |
Решим систему линейных уравнений отностительно x, y:
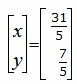 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
Кривые 2-го порядка: решения онлайн
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $\sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=\pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
http://matworld.ru/analytic-geometry/tochka-peresechenija-prjamyh.php
http://www.matburo.ru/ex_ag.php?p1=agk2