Найдите объем тела ограниченного поверхностями заданными уравнениями

Найдите объем тела ограниченного поверхностями заданными уравнениями

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Вычисление объёмов

Вычисление объёмов

1. Услуги проектирования
2. Двойной интеграл
3. Вычисление объёмов

Вычисление объёмов

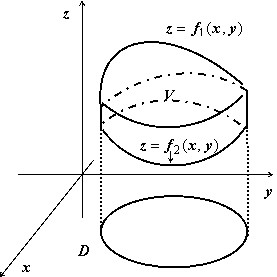
Объём тела, ограниченного сверху и снизу поверхностями $\mathbf < \textit < z >> =\mathbf < \textit < f >> _ < 1 >(\mathbf < \textit < x >> $,$\mathbf < \textit < y >> )$, $\mathbf < \textit < z >> =\mathbf < \textit < f >> _ < 2 >(\mathbf < \textit < x >> $,$\mathbf < \textit < y >> )$, $(x,y)\in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $\mathbf < \textit < Oz >> $, равен $v=\iint\limits_D < \left[ < f_1 (x,y)-f_2 (x,y) >\right]dxdy > $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

Найти объём тела $V:\left[ < \begin < l >y=0,\;z=0, \\ x+y+z=4,\; \\ 2x+z=4. \\ \end >\right.$

Решение:

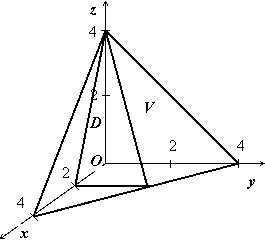
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $\mathbf < \textit < Oxz >> $:

$V:\left[ < \begin < l >(x,z)\in D, \\ 0\leqslant y\leqslant 4-x-z. \\ \end >\right.$

Область $\mathbf < \textit < D >> $ — треугольник, ограниченный прямыми $\mathbf < \textit < x >> $ = 0, $\mathbf < \textit < z >> $ = 0, 2$\mathbf < \textit < x >> +\mathbf < \textit < z >> $ = 4, поэтому

Найти объём области, ограниченной поверхностями $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < R >> ^ < 2 >$,

Решение:

Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $\mathbf < \textit < Oz >> $ < в уравнении нет $\mathbf < \textit < z >> $ в явной форме). Построить в плоскости $\mathbf < \textit < Oxy >> $ кривую шестого порядка, заданную уравнением $(\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >)^ < 3 >=\mathbf < \textit < R >> ^ < 2 >(\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >)$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей < чётные степени >и точка $\mathbf < \textit < О >> (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(\cos ^4\varphi +\sin ^4\varphi );r^2=R^2((\cos ^2\varphi +\sin ^2\varphi )^2-2\cos ^2\varphi \sin ^2\varphi )=R^2(1-\frac < \sin ^22\varphi > < 2 >)=$

$=R^2(1-\frac < 1-\cos 4\varphi > < 4 >)=R^2\frac < 3+\cos 4\varphi > < 4 >;r=R\frac < \sqrt < 3+\cos 4\varphi >> < 2 >.$ Эту кривую построить уже можно. $r(\varphi )$ максимально, когда $\cos 4\varphi =1\;(\varphi =0,\frac < 2\pi > < 4 >=\frac < \pi > < 2 >,\frac < 4\pi > < 4 >=\pi ,\frac < 6\pi > < 4 >=\frac < 3\pi > < 2 >)$, минимально, когда

$\cos 4\varphi =-1\;(\varphi =\frac < \pi > < 4 >,\frac < 3\pi > < 4 >,\frac < 5\pi > < 4 >,\frac < 7\pi > < 4 >),$ и гладко меняется между этими пределами < точка $\mathbf < \textit < О >> (0,0)$ не принадлежит этой кривой, где мы её потеряли? > .

Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Решение:

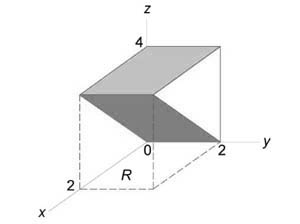
Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ < V = \iint\limits_R < \left[ < \left( < 4 - x >\right) — x >\right]dxdy > > = < \int\limits_0^2 < \left[ < \int\limits_0^2 < \left( < 4 - 2x >\right)dy > >\right]dx > > = < \int\limits_0^2 < \left[ < \left. < \left( < 4y - 2xy >\right) >\right|_ < y = 0 >^2 >\right]dx > > = < \int\limits_0^2 < \left( < 8 - 4x >\right)dx > > = < \left. < \left( < 8x - 2 < x^2 >>\right) >\right|_0^2 > = < 16 - 8 = 8. >$

Описать тело, объем которого определяется интегралом (V = \int\limits_0^1 < dx >\int\limits_0^ < 1 - x > < \left( < < x^2 >+ < y^2 >>\right)dy > .)

Решение:

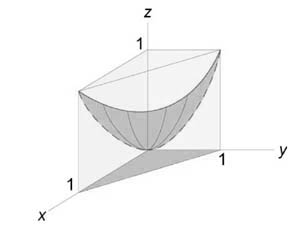
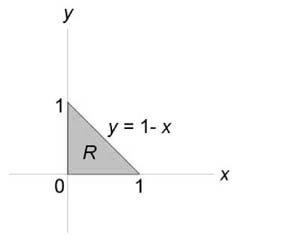
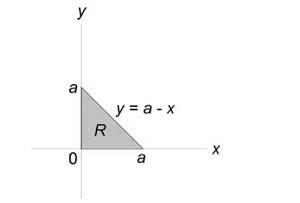
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = < x^2 >+ < y^2 >.) Объем тела равен $ < V = \int\limits_0^1 < dx >\int\limits_0^ < 1 - x > < \left( < < x^2 >+ < y^2 >>\right)dy > > = < \int\limits_0^1 < \left[ < \left. < \left( < < x^2 >y + \frac < < < y^3 >> > < 3 >>\right) >\right|_ < y = 0 >^ < 1 - x >>\right]dx > > = < \int\limits_0^1 < \left[ < < x^2 >\left( < 1 - x >\right) + \frac < < < < \left( < 1 - x >\right) > ^3 > > > < 3 >>\right]dx > > = \\ = < \int\limits_0^1 < \left( < < x^2 >— < x^3 >+ \frac < < 1 - 3x + 3 < x^2 >— < x^3 >> > < 3 >>\right)dx > > = < \int\limits_0^1 < \left( < 2 < x^2 >— \frac < < 4 < x^3 >> > < 3 >— x + \frac < 1 > < 3 >>\right)dx > > = < \left. < \left( < \frac < < 2 < x^3 >> > < 3 >— \frac < 4 > < 3 >\cdot \frac < < < x^4 >> > < 4 >— \frac < < < x^2 >> > < 2 >+ \frac < x > < 3 >>\right) >\right|_0^1 > = < \frac < 2 > < 3 >— \frac < 1 > < 3 >— \frac < 1 > < 2 >+ \frac < 1 > < 3 >= \frac < 1 > < 6 >. > $

Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

Решение:

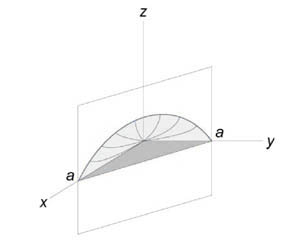
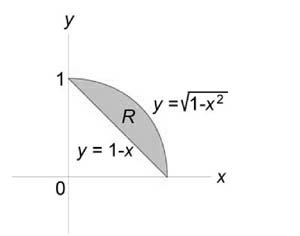
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( < x^2 >+ < y^2 >= 1,) (z = 1 — x.)

Решение:

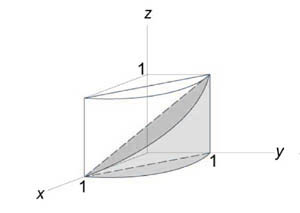
Как видно из рисунков, в области интегрирования (R) при (0 \le x \le 1) значения (y) изменяются от (1 — x) до (\sqrt < 1 - < x^2 >> .)

Вычислим второй интеграл ( < I_2 >= \int\limits_0^1 < x\sqrt < 1 - < x^2 >> dx > ,) используя замену переменной. Полагаем (1 — < x^2 >= w.) Тогда (-2xdx = dw) или (xdx = \large\frac < < - dw >> < 2 >\normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ < < I_2 >= \int\limits_0^1 < x\sqrt < 1 - < x^2 >> dx > > = < \int\limits_1^0 < \sqrt w \left( < - \frac < < dw >> < 2 >>\right) > > = < - \frac < 1 > < 2 >\int\limits_1^0 < \sqrt w dw >> = < \frac < 1 > < 2 >\int\limits_0^1 < \sqrt w dw >> = < \frac < 1 > < 2 >\int\limits_0^1 < < w^ < \large\frac < 1 > < 2 >\normalsize > > dw > > = < \frac < 1 > < 2 >\left. < \left( < \frac < < 2 < w^ < \large\frac < 3 > < 2 >\normalsize > > > > < 3 >>\right) >\right|_0^1 = \frac < 1 > < 3 >. > $ Наконец, вычислим третий интеграл. $\require < cancel > < < I_3 >= \int\limits_0^1 < \left( < 1 - 2x + < x^2 >>\right)dx > > = < \left. < \left( < x - < x^2 >+ \frac < < < x^3 >> > < 3 >>\right) >\right|_0^1 > = < \cancel < 1 >— \cancel < 1 >+ \frac < 1 > < 3 >= \frac < 1 > < 3 >. > $ Таким образом, объем тела равен $ < V = < I_1 >— < I_2 >— < I_3 >> = < \frac < \pi > < 4 >— \frac < 1 > < 3 >— \frac < 1 > < 3 >= \frac < \pi > < 4 >— \frac < 2 > < 3 >\approx 0,12. > $

Вычислить объем единичного шара.

Решение:

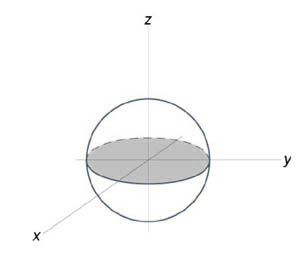
Уравнение сферы радиусом (1) имеет вид ( < x^2 >+ < y^2 >+ < z^2 >= 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = \sqrt < 1 - \left( < < x^2 >+ < y^2 >>\right) > .$ Преобразуя это уравнение в полярные координаты, получаем $z\left( < r,\theta >\right) = \sqrt < 1 - < r^2 >> .$ В полярных координатах область интегрирования (R) описывается множеством (R = \left[< \left( < r,\theta >\right)|\;0 \le r \le 1,0 \le \theta \le 2\pi >\right].) Следовательно, объем верхнего полушара выражается формулой $ < < V_ < \large\frac < 1 > < 2 >\normalsize > > = \iint\limits_R < \sqrt < 1 - < r^2 >> rdrd\theta > > = < \int\limits_0^ < 2\pi > < d\theta >\int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > > = < 2\pi \int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > . > $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — < r^2 >= t.) Тогда (-2rdr = dt) или (rdr = — \large\frac < < dt >> < 2 >\normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ < < V_ < \large\frac < 1 > < 2 >\normalsize > > = 2\pi \int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > > = < 2\pi \int\limits_1^0 < \sqrt t \left( < - \frac < < dt >> < 2 >>\right) > > = < - \pi \int\limits_1^0 < \sqrt t dt >> = < \pi \int\limits_0^1 < < t^ < \large\frac < 1 > < 2 >\normalsize > > dt > > = < \pi \left. < \left( < \frac < < < t^ < \large\frac < 3 > < 2 >\normalsize > > > > < < \frac < 3 > < 2 >> > >\right) >\right|_0^1 > = < \frac < < 2\pi >> < 3 >. > $ Таким образом, объем единичного шара равен $V = 2 < V_ < \large\frac < 1 > < 2 >\normalsize > > = \frac < < 4\pi >> < 3 >.$

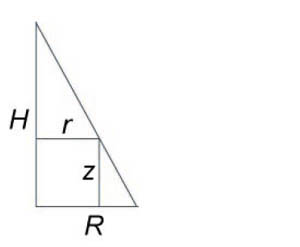
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Решение:

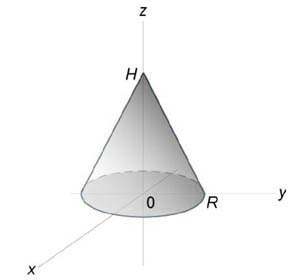
Далее:

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Вычисление объёмов

Теорема об аналоге СДНФ в Pk

Свойства тройного интеграла

Равносильные формулы алгебры высказываний

Дифференциальные характеристики векторного поля

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Критерий полноты <формулировка>. Лемма о несамодвойственной функции

Лемма о построении множества $[F]_$

Булевы функции от $n$ переменных

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Выражение площади плоской области через криволинейный интеграл

Определение двойного интеграла

Соленоидальное векторное поле

Огравление $\Rightarrow $

Примеры решений тройных интегралов

В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:

Тройные интегралы: примеры решений

Задача 1. Вычислить тройной интеграл

$$\iiint_V x^2yz dx dy dz, \quad V: -1 \le x \le 2, 0\le y \le 3, 2 \le z \le 3. $$

Задача 2. Переходя к сферическим координатам, вычислить интеграл

$$\iiint_V x^2 dxdydz, \quad V: x^2+y^2+z^2=R^2,\, z\ge 0, x\gt 0.$$

Задача 3. Переходя к цилиндрическим координатам вычислить интеграл

$$\iiint_V x^2 dxdydz, \quad V: x^2+y^2=x,\, z=x^2+y^2, z=0.$$

Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)

Трудности с задачами? МатБюро поможет с интегралами.

Объемы тел: примеры решений

Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).

Задача 6. Найти объем тела, ограниченного поверхностями

Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:

Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью

Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.

Моменты, масса тела: примеры решений

Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью $$(x^2+y^2+z^2 )^3=\frac $$ с плотностью $z=0$ $(z \ge 0)$.

Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $\gamma(\rho)$, где $\rho$ – полярный радиус точки.

Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $\mu$.

Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.