Найдите площадь поверхности сферы заданной уравнением

Вычисление площади поверхности

Вычисление площади поверхности

1. Услуги проектирования
2. Двойной интеграл
3. Вычисление площади поверхности

Вычисление площади поверхности

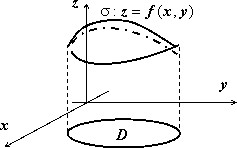
Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf < \textit < D >> $ на плоскости $\mathbf < \textit < Оху >> $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой

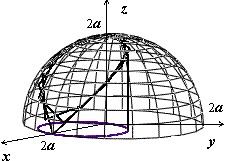
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >$ = 2$\mathbf < \textit < ax >> $ из сферы $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >$ = 4$\mathbf < \textit < a >> ^ < 2 >$ .

Решение:

Область $\mathbf < \textit < D >> $ — сдвинутый на $\mathbf < \textit < а >> $ единиц по оси $\mathbf < \textit < Ох >> $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf < \textit < Оху >> $ и $\mathbf < \textit < Охz >> $:

Вычислить площадь cферы радиуса (a.)

Решение:

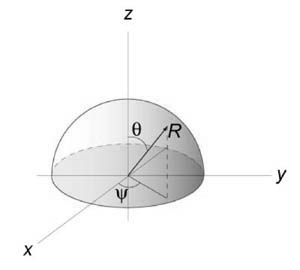
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ < < x^2 >+ < y^2 >+ < z^2 >= < a^2 >> \;\; < \text < или >\;\;z = \sqrt < < a^2 >— < x^2 >— < y^2 >> . > $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ < S_ < \large\frac < 1 > < 2 >\normalsize > > = \iint\limits_R < \sqrt < 1 + < < \left( < \frac < < \partial z >> < < \partial x >> >\right) > ^2 > + < < \left( < \frac < < \partial z >> < < \partial y >> >\right) > ^2 > > dxdy > .$

Площадь поверхности полной сферы, соответственно, равна $S = 2 < S_ < \large\frac < 1 > < 2 >\normalsize > > = 4\pi < a^2 >.$

Далее:

Вычисление площадей плоских областей

Определение двойного интеграла

Специальные векторные поля

Поверхностный интеграл первого рода и его свойства

Вычисление объёмов

Определение криволинейного интеграла второго рода

Вычисление криволинейного интеграла второго рода. Примеры.

Поверхностный интеграл второго рода и его свойства

Критерий полноты <формулировка>. Лемма о нелинейной функции

Частные случаи векторных полей

Критерий полноты <формулировка>. Лемма о немонотонной функции

Вычисление двойного интеграла

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Примеры применения цилиндрических и сферических координат

Огравление $\Rightarrow $

Формулы площади поверхности геометрических фигур

Применение формулы

Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.

Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.

Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.

Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x – x ₀) 2 + ( y – y ₀) 2 + ( z – z ₀) 2 = R 2

3. Параметрическое уравнение сферы с центром в точке ( x ₀, y ₀, z ₀):
x = x ₀ + R · sin θ · cos φ y = y ₀ + R · sin θ · sin φ z = z ₀ + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].

Площадь прямоугольного параллелепипеда

Формула площади поверхности прямоугольного параллелепипеда:

Шар, сфера и их части

Введем следующие определения, связанные с шаром, сферой и их частями.

Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).

Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).

Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.

Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).

Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .

Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .

По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).

Высотой шарового сектора называют высоту его сферического сегмента .

Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .

Трактовка значений

Это следует знать:

• Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
• Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
• Число «пи» – это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
• Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
• Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
• Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
• Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.

Введите радиус сферы:

Сфера – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.

Площадь поверхности сферы формула:
S = 4 π R 2 , где R – радиус сферы, π – число пи

Через диаметр

Как известно, диаметр шара равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:

S = 4 π (d/2) 2

Терминология и сферическая геометрия

Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).

Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).

Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.

Задача 36965 1) найти площадь см. картинка 3) дано.

Условие

1) найти площадь см. картинка

3) дано уравнение сферы
(x-2)^2 + y^2 + (z+2)^2 =16
Найти координаты центра сферы, радиус и площадь поверхности.

5) Диагональ осевого сечения цилиндра равна 8 см и образует с плоскостью основания цилиндра угол 60 ° . Найти площадь полной поверхности цилиндра.

Все решения

1.
При вращении прямоугольника вокруг стороны 9 получается цилиндр

r=3
h=9
S_(цилиндра вращения)=2πrh=2π*3*9=54π

3.
(2;0;-2)- координаты центра
R=4

2r=4 — катет, против угла в 30 градусов равен половине гипотенузы