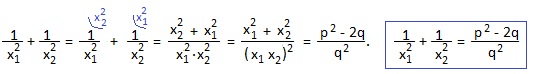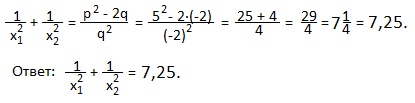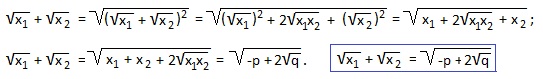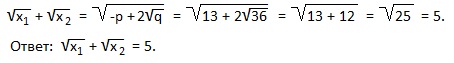Найдите сумму всех вещественных корней уравнения

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.

Кубическим уравнением называется уравнение вида

• ax 3 + bx 2 + cx +d = 0 , (1)
• где a, b,c ,d — постоянные коэффициенты, а х — переменная.

Мы рассмотрим случай, когда коэффициенты являются веществеными числами.

Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.

Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.

Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:

Δ= -4b 3 d + b 2 c 2 — 4ac 3 + 18abcd — 27a 2 d 2 (Да, это дискриминант кубического уравнения)

Итак, возможны только 3 следующих случая:

• Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
• Δ 3 + py + q = 0 (2)

К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:

• x= y — b/3a (3)
• p= — b 2 /3a 2 + c/a
• q= 2b 3 /27a 3 — bc/3a 2 + d/a

Итак, приступим к вычислению корней. Найдем следующие величины:

Дискриминант уравнения (2) в этом случае равен

Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:

Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y₁. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y₂, y₃ и подставьте их в (3).

Если Q 3 + ax 2 + bx +c = 0 (4)

Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.

Итак, алгоритм применения этой формулы:

3. a) Если S>0, то вычисляем

И наше уравнение имеет 3 корня (вещественных):

Тогда единственный корень (вещественный): x₁= -2sgn(R)*|Q| 1/2 *ch(φ) — a/3

Для тех, кого интересуют также и мнимые корни:

• ch(x)=(e x +e -x )/2
• Arch(x) = ln(x + (x 2 -1) 1/2 )
• sh(x)=(e x -e -x )/2
• sgn(x) — знак х

в) Если S=0,то уравнение имеет меньше трех различных решений:

Консультации и техническая
поддержка сайта: Zavarka Team

Найдите сумму вещественных корней уравнения?

Математика | 5 — 9 классы

Найдите сумму вещественных корней уравнения.

Указание : сделать замену переменной (x — 4)(x — 5)(x — 6)(x — 7) = 1680.

Умножаете первую скобку на четвёртую, а вторую на третью, получаете

x² — 11x заменяете на t.

(t + 28)(t + 30) = 1680 Раскрываете скобки, находите t.

T² + 58t + 840 — 1680 = 0

D = 3364 + 3360 = 6724 = 82²

x² — 11x = — 70 или х² — 11х = 12

х² — 11х + 70 = 0 х² — 11х — 12 = 0

D&lt ; 0 вещественных х1 = — 1, х2 = 12

корней нет Сумма — 1 + 12 = 11.

Найдите все значения параметра b, при которых уравнение имеет два разных вещественных (дійсних) корня?

Найдите все значения параметра b, при которых уравнение имеет два разных вещественных (дійсних) корня.

1. запиши четыре суммы, в которых сложение можно заменить умножение, и столько же сумм, в которых этого сделать нельзя ?

1. запиши четыре суммы, в которых сложение можно заменить умножение, и столько же сумм, в которых этого сделать нельзя .

2. Где можно, замени сложение умножением.

Найди значение выражений.

1) Запиши четыре суммы, в которых сложение можно заменить умножением, и столько же сумм, в которых этого сделать нельзя?

1) Запиши четыре суммы, в которых сложение можно заменить умножением, и столько же сумм, в которых этого сделать нельзя.

2) Где можно, замени сложение умножением.

Найди значения выражений.

Найдите сумму корней уравнения?

Найдите сумму корней уравнения.

Помогите, запиши 4 суммы, в которых сложение можно заменить умножением, и столько же сумм, в которых этого сделать нельзя?

Помогите, запиши 4 суммы, в которых сложение можно заменить умножением, и столько же сумм, в которых этого сделать нельзя.

2) где можно, замени сложение умножением.

Найди значения выражений.

Найдите сумму корней уравнения ?

Найдите сумму корней уравнения :

Найдите сумму корней уравнения?

Найдите сумму корней уравнения.

Найдите сумму корней уравнения |x² + 5x| = 6?

Найдите сумму корней уравнения |x² + 5x| = 6.

Найдите сумму корней уравнения?

Найдите сумму корней уравнения.

СРОЧНО найдите сумму корней уравнения?

СРОЧНО найдите сумму корней уравнения.

Вопрос Найдите сумму вещественных корней уравнения?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

2)Вероятность того, что один из вытащенных шаров будет белым равна количеству шансов вытащить белый шар из всей суммы шаров, находящихся в урне. Этих шансов ровно столько сколько белых шаров в урне, а сумма всех шансов равна сумме белых и черных шар..

56 — 6 = 50 скорость снегохода 59 : 2 = 25 скорость упряжки 50 + 25 = 75 скорость упряжки и снегохода 75 : 1. 5 = 50км Ответ : 50КМ.

8.2.4. Применение теоремы Виета

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

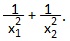
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

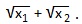
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!