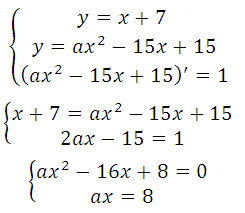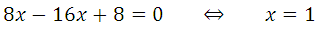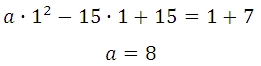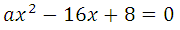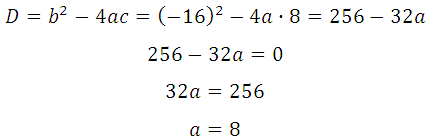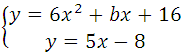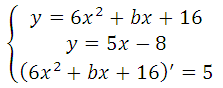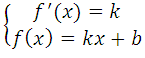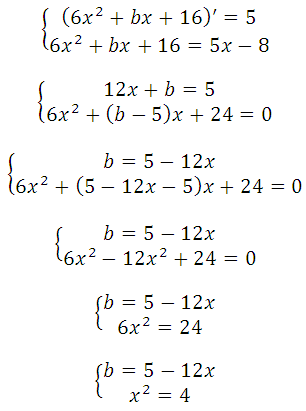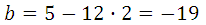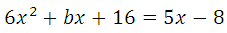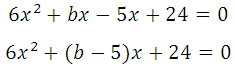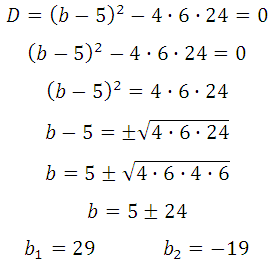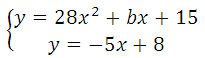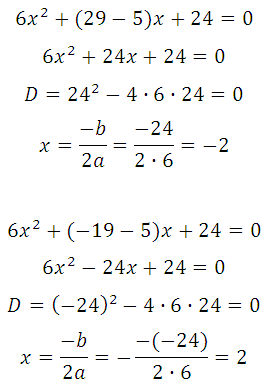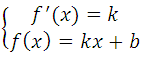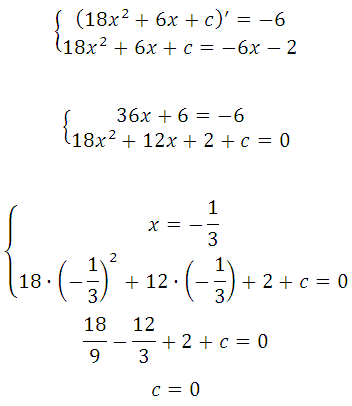Найдите уравнение параболы касающейся прямой в точке

Парабола и касательная. Находим a,b,c!

Здравствуйте! Продолжаем рассматривать задачи входящие в состав экзамена по математике. Задания, которые мы рассмотрим ниже, по-большому счёту, никаких глубоких знаний теории не требуют. Для их решения необходимо понимание геометрического смысла производной , умение решать квадратное уравнение и немного логики.

Суть заданий следующая: дана парабола вида у = ах 2 +bх+c и касательная к этой параболе у=kх+b. Один из коэффициентов (a, b или c) неизвестен и его необходимо найти.

Как решать такие задачи? Что необходимо вспомнить?

1. Если даны уравнения двух функций, то точка (точки) пересечения их графиков находится путём решения системы этих уравнений. Пара (х;у) являющаяся решением системы есть точка пересечения графиков (или пары, если точек пересечения больше).

2. Если к графику функции проведена касательная, то производная этой функции в точке касания равна угловому коэффициенту этой касательной (см. ссылку выше).

Рассмотрим задачи (показаны два способа решения):

Прямая у=х+7 является касательной к графику функции ах 2 –15х+15. Найдите a.

Прямая и график данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения (кроме неизвестных х и у имеется ещё параметр а).

Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x_o) = k. Это третье уравнение, запишем систему:

Подставим из второго уравнения в первое:

Найдём а, подставим х = 1 в ах 2 – 15х + 15 = х + 7 или в 2ах – 15 = 1

По смыслу задачи параметр a ≠ 0, график заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах 2 – 15х + 15 = х + 7 имело единственно решение:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Прямая у=3х+1 является касательной к графику функции ах 2 +2х+3. Найдите a.

Прямая у=5х–8 является касательной к графику функции 6х 2 + bх + 16

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая и парабола пересекаются в одной точке, поэтому оба уравнения можно внести в систему, но она не решаема, так как имеем три неизвестных:

Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x o ) = k. Это третье уравнение, запишем систему:

Кратко можно сказать так:

Условия касания графика функции f (x) = k и прямой у = kх + b задаётся системой требований:

По условию, абсцисса точки касания положительна, значит х = 2.

График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение

имело единственно решение. Преобразуем:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Теперь определим, при каком значении b абсцисса точки касания будет больше нуля. Можно подставить поочерёдно полученные значения в систему:

Далее решить её и сдать вывод. Верным решением будет то значение b, при котором получим положительную абсциссу.

Но мы сразу подставим их (поочерёдно) в 28х 2 + (b – 5) + 24 = 0.

Таким образом, b = – 19 (при этом значении абсцисса точки касания положительна).

Прямая у = –5х+8 является касательной к графику функции 28х 2 + bх + 15.

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая у=–6х–2 является касательной к графику ф-ии 18х 2 +6х+с. Найдите c.

Условия касания графика функции у = f (x) и прямой у = kx + b задаётся системой требований:

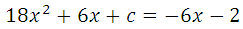
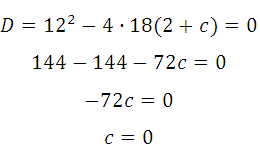
График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение имело единственное решение, преобразуем: Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю, значит: Ответ: 0

Прямая у=3х+4 является касательной к графику функции 3х 2 –3х+с. Найдите c.

Как видим, понимание способа нахождения точки пересечения графиков функций, заключающееся в решении системы, пригодилось при решении указанных задач (на ЕГЭ могут быть и другие). Но какие бы они не были, если чётко уясните геометрический смысл производной, проблем с подобными у вас не будет.

В данной рубрике продолжим рассматривать задачи, не пропустите!

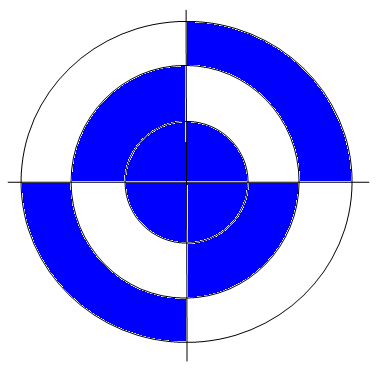
Имеется круглая мишень радиуса R. На ней отмечены две окружности, радиусы которых равны 1/3 и 2/3 от радиуса мишени. Какова вероятность того, что кинутый в мишень дротик попадёт в закрашенную часть мишени? Результат округлите до тысячных.

*Учесть, что дротик мимо мишени попасть не может.

Тот учащийся, который первый напишет верный ответ, получит поощрительный приз в размере 150 рублей 😉

Надеюсь материал был вам полезен. Успехов Вам!

Найдите уравнение параболы касающейся прямой в точке

Глава 20. Парабола

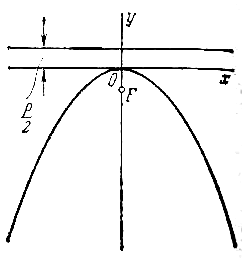
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

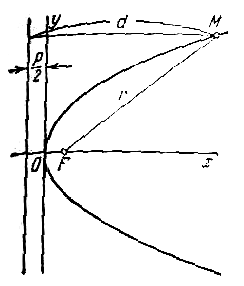
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

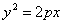
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

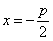
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

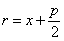
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

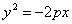
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

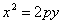
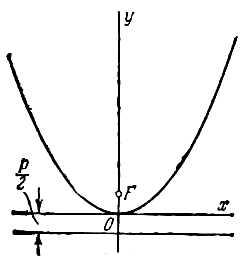
если она лежит в верхней полуплоскости (рис.), и

(4)

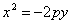
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.