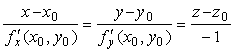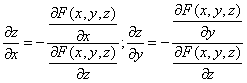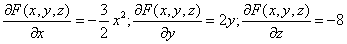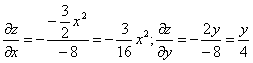Найдите вектор нормали плоскости заданной уравнением

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

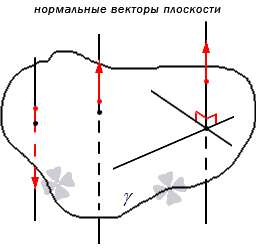
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Нормальный вектор плоскости, координаты нормального вектора плоскости.

Хорошее представление о прямой линии начинается с момента, когда вместе с ее образом одновременно возникают образы ее направляющих и нормальных векторов. Аналогично, при упоминании о плоскости в пространстве, она должна представляться вместе со своим нормальным вектором. Почему так? Да потому что во многих случаях удобнее использовать нормальный вектор плоскости, чем саму плоскость.

В этой статье мы сначала дадим определение нормального вектора плоскости, приведем примеры нормальных векторов и необходимые графические иллюстрации. Далее поместим плоскость в прямоугольную систему координат в трехмерном пространстве и научимся определять координаты нормального вектора плоскости по ее уравнению.

Навигация по странице.

Нормальный вектор плоскости – определение, примеры, иллюстрации.

Для хорошего усвоения материала нам потребуется хорошее представление о прямой в пространстве, представление о плоскости и определения из статьи векторы – основные определения.

Дадим определение нормального вектора плоскости.

Нормальный вектор плоскости — это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.

Из определения следует, что существует бесконечное множество нормальных векторов данной плоскости.

Так как все нормальные векторы заданной плоскости лежат на параллельных прямых, то все нормальные векторы плоскости коллинеарны. Другими словами, если — нормальный вектор плоскости , то вектор при некотором ненулевом действительном значении t также является нормальным вектором плоскости (смотрите статью условие коллинеарности векторов).

Также следует заметить, что любой нормальный вектор плоскости можно рассматривать как направляющий вектор прямой, перпендикулярной к этой плоскости.

Множества нормальных векторов параллельных плоскостей совпадают, так как прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и ко второй плоскости.

Из определения перпендикулярных плоскостей и определения нормального вектора плоскости следует, что нормальные векторы перпендикулярных плоскостей перпендикулярны.

Приведем пример нормального вектора плоскости.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz . Координатные векторы являются нормальными векторами плоскостей Oyz , Oxz и Oxy соответственно. Это действительно так, потому что векторы ненулевые и лежат на координатных прямых Ox , Oy и Oz соответственно, которые перпендикулярны координатным плоскостям Oyz , Oxz и Oxy соответственно.

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.

Озвучим цель, которая преследовалась при создании этого пункта статьи: научиться находить координаты нормального вектора плоскости, если известно уравнение плоскости в прямоугольной системе координат Oxyz .

Общее уравнение плоскости вида определяет в прямоугольной системе координат Oxyz плоскость, нормальным вектором которой является вектор . Таким образом, чтобы найти координаты нормального вектора плоскости нам достаточно иметь перед глазами общее уравнение этой плоскости.

Рассмотрим несколько примеров.

Найдите координаты какого-либо нормального вектора плоскости .

Нам дано общее уравнение плоскости, коэффициенты перед переменными x , y и z представляют собой соответствующие координаты нормального вектора этой плоскости. Следовательно, — один из нормальных векторов заданной плоскости. Множество всех нормальных векторов этой плоскости можно задать как , где t — произвольное действительное число, отличное от нуля.

Плоскость задана уравнением . Определите координаты ее направляющих векторов.

Нам дано неполное уравнение плоскости. Чтобы стали видны координаты ее направляющего вектора, перепишем уравнение в виде . Таким образом, нормальный вектор этой плоскости имеет координаты , а множество всех нормальных векторов запишется как .

Уравнение плоскости в отрезках вида , как и общее уравнение плоскости, позволяет сразу записать один из нормальных векторов этой плоскости – он имеет координаты .

В заключении скажем, что с помощью нормального вектора плоскости могут быть решены различные задачи. Самыми распространенными являются задачи на доказательство параллельности или перпендикулярности плоскостей, задачи на составление уравнения плоскости, а также задачи на нахождение угла между плоскостями и на нахождение угла между прямой и плоскостью.