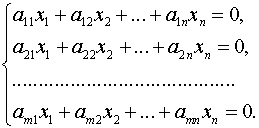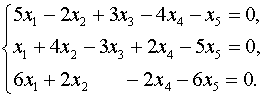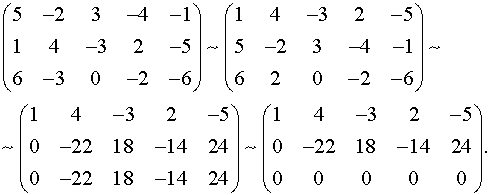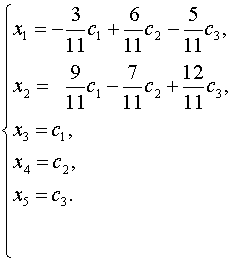Найти базис линейного пространства решений систем уравнений

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3

Системы линейных однородных уравнений

Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы

1. Записываем матрицу системы:

и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:

.

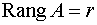
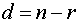
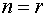
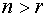
Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.

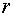
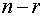
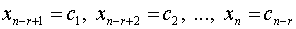
2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.

3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.

Примечание. К элементарным преобразованиям матрицы относят:

1. умножение (деление) строки на множитель, отличный от нуля;

2. прибавление к какой-либо строке другой строки, умноженной на любое число;

3. перестановка строк местами;

4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).

Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:

Полагаем , тогда

.

Размерность линейного пространства решений равна 3.

:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон

Размерность и базис линейного пространства

Определения размерности и базиса

Линейное пространство называется n-мерным , если в нем существует система из линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число называется размерностью (числом измерений) линейного пространства и обозначается . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве найдется система, состоящая из линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.

Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов ( базисных векторов ).

Теорема 8.1 о разложении вектора по базису. Если — базис n-мерного линейного пространства , то любой вектор может быть представлен в виде линейной комбинации базисных векторов:

и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.

Действительно, размерность пространства равна . Система векторов линейно независима (это базис). После присоединения к базису любого вектора , получаем линейно зависимую систему (так как это система состоит из векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.

Следствие 1. Если — базис пространства , то , т.е. линейное пространство является линейной оболочкой базисных векторов.

В самом деле, для доказательства равенства двух множеств достаточно показать, что включения и выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. . Отсюда следует равенство рассматриваемых множеств.

Следствие 2. Если — линейно независимая система векторов линейного пространства и любой вектор может быть представлен в виде линейной комбинации (8.4): , то пространство имеет размерность , а система является его базисом.

В самом деле, в пространстве имеется система линейно независимых векторов, а любая система из большего количества векторов n)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEAAAAAWBAMAAACCkIcHAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAX1hEMCpIZfQQeAxUfDvHPe4AAABRklEQVQoz2NgIAyYD+CS4TUAU2YMDBbBWBUwxoJI9icMDFd/YTfCuwBIsCowMLB9xK6ALQFInHdgYJAOBPOZFqIpYP8OJDoFGBjqFcB8Fk1DNEc8AuIIIMN+gUcMigqWtgNmQBcypgHxJyA/XyYrDCKhrQKmOVY8M9QHel8PqOAvEG894fQJaqglWIWk2C+G9QsYGPUFGNiBPmT/2cCyAGatZQuQrJUOYACZYC/AwAJUwPz1GTw0GU1TQFS9AmO0AFgByAq2j94T4Aa0g2n7BSw/gBTQCpAjpQNYNxpBHAlxAtDZAsx/PBkYgY5kiACZxxoQDvEmVJ5xKwPHA2UGhlQgW1MA6F7mZwaoAfWJgfdHAwPjJpBzHBh4GBjcwb5HBCQwllygQS2mgDupcAQACZ4tuBX4FUATDC4ASUdMF3DJMxkQkWIB7TREH/AzV/MAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы . Значит, и — базис .

Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства можно дополнить до базиса пространства.

В самом деле, пусть — линейно независимая система векторов n-мерного пространства . Рассмотрим линейную оболочку этих векторов: . Любой вектор образует с векторами линейно зависимую систему , так как вектор линейно выражается через остальные. Поскольку в n-мерном пространстве существует линейно независимых векторов, то и существует вектор , который не принадлежит . Дополняя этим вектором линейно независимую систему , получаем систему векторов , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что , а это противоречит условию . Итак, система векторов линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: . Если , то — базис и теорема доказана. Если , то дополняем систему вектором и т.д. Процесс дополнения обязательно закончится, так как пространство конечномерное. В результате получим равенство , из которого следует, что — базис пространства . Теорема доказана.

1. Базис линейного пространства определяется неоднозначно. Например, если — базис пространства , то система векторов при любом также является базисом . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.

2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.

3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.

4. Если множество является линейной оболочкой , то векторы называют образующими множества . Следствие 1 теоремы 8.1 в силу равенства позволяет говорить, что базис — это минимальная система образующих линейного пространства , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора ) без нарушения равенства .

5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы . Количество базисных векторов определяет размерность пространства . Разумеется, что эти определения эквивалентны приведенным выше.

Примеры базисов линейных пространств

Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.

1. Нулевое линейное пространство не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: . Это пространство не имеет базиса.

2. Пространства имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, , а базисом пространства является любой ненулевой вектор. Аналогично доказывается, что и . Базисом пространства служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в является единичный вектор на прямой. Стандартным базисом в считается базис , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве считается базис , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.

3. Пространство содержит не более, чем , линейно независимых векторов. В самом деле, возьмем столбцов из и составим из них матрицу размеров . Если n» png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQCAMAAACIsme9AAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMActEwobEQRsAhMfCRYeCBZdtIVwAAAMRJREFUKM+dkdsSwyAIRJUKivHC/39tJY6Npplm0jxEHT3A7hrzx/dyAZ8RnOUhYaLYh4SVOA9Z+ZbAbTn64O6YDfVZWhhvzlWIU/t9ZCSblkbehZkhJEHHBDhkpGhkOzk4MzazQFtDf4SCTXmkL9ddGYynLLovocsAKFf2coKji5MjBl1Wf8dUeTru1ZPwSMO3nrCEuio3LFUxaIpUhlHC19lLPLnbZUglrVuaY822QL8SrLtJGECn77dxGugicer19OYNWVcGI0RZra4AAAAASUVORK5CYII=» />, то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, . В пространстве не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы

линейно независимы. Следовательно, . Пространство называется n-мерным вещественным арифметическим пространством . Указанный набор векторов считается стандартным базисом пространства . Аналогично доказывается, что , поэтому пространство называют n-мерным комплексным арифметическим пространством .

4. Напомним, что любое решение однородной системы можно представить в виде , где , a — фундаментальная система решений. Следовательно, , т.е. базисом пространства решений однородной системы служит ее фундаментальная система решений, а размерность пространства , где — количество неизвестных, а — ранг матрицы системы.

5. В пространстве матриц размеров можно выбрать 6 матриц:

которые линейно независимы. Действительно, их линейная комбинация

равна нулевой матрице только в тривиальном случае . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из линейным образом выражается через выбранные 6 матриц, т.е. . Следовательно, , а матрицы являются базисом (стандартным) этого пространства. Аналогично доказывается, что .

6. Для любого натурального в пространстве многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены линейно независимы, так как их линейная комбинация

равна нулевому многочлену только в тривиальном случае . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства многочленов с действительными коэффициентами. Пространство многочленов степени не выше, чем , конечномерное. Действительно, векторы образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из можно представить в виде линейной комбинации этих векторов:

7. Пространство непрерывных функций является бесконечно мерным. Действительно, для любого натурального многочлены , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).

В пространстве тригонометрических двучленов (частоты ) с действительными коэффициентами базис образуют одночлены . Они линейно независимы, так как тождественное равенство возможно только в тривиальном случае . Любая функция вида линейно выражается через базисные: .

8. Пространство действительных функций, определенных на множестве , в зависимости от области определения может быть конечномерным или бесконечномерным. Если — конечное множество, то пространство конечномерное (например, ). Если — бесконечное множество, то пространство бесконечномерное (например, пространство последовательностей).

9. В пространстве любое положительное число , не равное единице, может служить базисом. Возьмем, например, число . Любое положительное число можно выразить через , т.е. представить в виде , где . Следовательно, размерность этого пространства равна 1, а число является базисом.

10. Пусть — базис вещественного линейного пространства . Определим на линейные скалярные функции , положив:

При этом, в силу линейности функции , для произвольного вектора получаем .

Итак, определены элементов (ковекторов) сопряженного пространства . Докажем, что — базис .

Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов и приравняем ее нулевой функции

Подставляя в это равенство , получаем . Следовательно, система элементов пространства линейно независима, так как равенство возможно только в тривиальном случае.

Во-вторых, докажем, что любую линейную функцию можно представить в виде линейной комбинации ковекторов . Действительно, для любого вектора в силу линейности функции получаем:

т.е. функция представлена в виде линейной комбинации функций (числа — коэффициенты линейной комбинации). Следовательно, система ковекторов является базисом сопряженного пространства и (для конечномерного пространства ).

21. Пространство решений системы линейных однородных уравнений

Пусть дана система (30) линейных однородных уравнений с коэффициентами из поля Р.

(30)

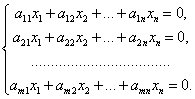
Так как столбец свободных членов в матрице А1 этой системы состоит только из нулей, то rang A = rang A1, т. е. система линейных однородных уравнений всегда совместна. В частности она всегда имеет нулевое решение. Рассмотрим множество всех возможных решений системы (30).

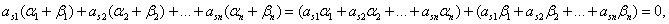
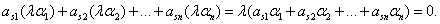
Пусть A =(A1, A2, … , An) и B =(B1, B2, … , Bn) – Любые два из них. Их можно рассматривать, как векторы в арифметическом n-мерном пространстве над полем Р. Пусть L – любой элемент поля Р. Тогда A +B = (A1 + B1, A2 + B2, … , An + Bn ), L×A = (LA1, LA2, … , LAn). Подставим компоненты этих векторов в произвольное S-е уравнение системы (30). Получим Итак, если A и B – Любые два решения системы (30) и L – любой элемент поля Р, то A +B И L×A тоже являются решением этой системы. Но тогда из теоремы 14 следует

Теорема 27. Множество решений системы линейных однородных уравнений с N Переменными есть линейное подпространство арифметического пространства Аn .

Теорема 28. Размерность пространства решений системы линейных однородных уравнений равна N – r, Где N – Число неизвестных, r – ранг матрицы системы.

Доказательство. Пусть L – пространство решений системы (30). Тогда L Ì Аn . Пусть A = (A1, A2, … Ar, Ar+1, … , An) – произвольное решение системы. Пусть (Ar+1, … , An) – набор свободных неизвестных, соответствующий этому решению. Множество всех возможных наборов свободных неизвестных есть арифметическое (N – r)-мерное пространство Аn–r . Зададим отображение J: L ® Аn–r по правилу

Покажем, что J – изоморфизм (определение 24). Для этого нужно проверить три условия.

1. Покажем, что J – взаимнооднозначное отображение. Решению A = (A1, A2, … Ar, Ar+1, … , An) соответствует только один набор (Ar+1, … , An), следовательно, J – Однозначное отображение. Обратно, если задать элемент (Ar+1, … , An) из Аn–r , то по теореме Крамера найдётся только один набор (A1, A2, … Ar ) искомых неизвестных, т. е. каждый элемент J(A) из Аn–r соответствует единственному элементу из L .

Итак, пространство решений системы линейных однородных уравнений изоморфно арифметическому (N – r)-мерному пространству. Следовательно, размерность L равна (N – r).

Определение 29. Базис пространства решений системы линейных однородных уравнений называется её Фундаментальной системой решений.

Так как при изоморфизме базис пространства Аn–r соответствует базису пространства L , То для того. чтобы найти фундаментальную систему решений для системы (30), достаточно выбрать (N – r) линейно независимых наборов свободных неизвестных и для каждого из них найти решение данной системы.

Следствие. Если А1, а2, …, аN–r фундаментальная система решений системы линейных однородных уравнений (30) и С1, С2, … , СN–r – произвольные элементы поля Р, то С1А1 + С2А2 + … + СN–r АN–r – общее решение этой системы.