Калькулятор периметра эллипса
Введите длину большой и малой полуосей эллипса, укажите точность расчета и нажмите «Посчитать». Калькулятор выполнит расчет периметра эллипса (расчет приблизительный).
Калькулятор
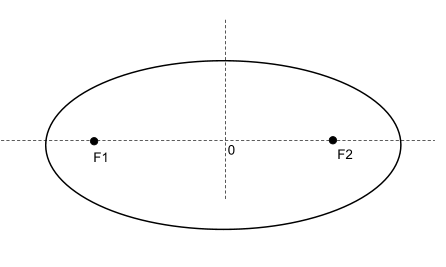
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости есть величина постоянная, больше расстояния между F1 и F2.
Точки F1 и F2 называют фокусами эллипса, а расстояние между ними — фокусным расстоянием.
Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a.
Отрезок, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Формулу периметра эллипса нельзя выразить при помощи простейших функций.
Нахождение длины дуги эллипса
IP76 > Нахождение длины дуги эллипса
Как ни странно, но для нахождения длины дуги эллипса нет какой-то определенной функции, как в случае длины дуги окружности, или нахождения координат точки на эллипсе. Это интегральное уравнение.
Калькулятор
Get a better browser, bro…
Интегральное уравнение будем решать как обычно делается в подобных случаях: суммировать очень маленькие значения, которые получаются в результате работы некоей функции, на заданном диапазоне данных, которые наращиваются на чрезвычайно малую постоянную величину. Эта малая величина задается вызывающей стороной. В конце статьи есть рабочий пример с исходниками, в котором можно поиграться с этой «малостью».
Длина дуги, как сумма хорд
Самое простое, что может прийти в голову, это двигаться от начала дуги к ее концу с небольшим наращиванием угла отклонения, считать хорду и прибавлять ее к накапливаемой сумме.


Проще говоря, находим координаты двух точек на эллипсе, отстоящих друг от друга на некий малый угол, по ним находим хорду, как гипотенузу получившегося прямоугольного треугольника.
В коде выглядит так:
Проверим с планетарным размахом. По последним данным Международной Службы Вращения Земли (IERS — 1996) большая экваториальная полуось Земли равна 6 378 136,49 м, а полярная малая — 6 356 751,75 м.
Посчитаем периметр меридиана каким-нибудь онлайн-калькулятором, получаем 40 007 859.543 (некоторые могут дать другое число, т.к. используют приближенные формулы для вычисления периметра).
Представленная выше функция за 109 милисекунд выдала результат 40 007 996.265 при дельте 0.001. Это нельзя назвать точным результатом.
Длина дуги, как интеграл
Длиной некоторой дуги называется тот предел, к которому стремится длина вписанной ломаной, когда длина наибольшего ее звена стремится к нулю:


Таким образом, длина дуги эллипса может быть описана интегральным уравнением:

Используя параметрическое уравнение эллипса, приходим к уравнению:
Где t1 и t2 – параметры для начала и конца дуги параметрического уравнения эллипса. Параметром является некий угол к оси абсцисс. Что такое и как найти параметр для угла эллипса подробно изложено тут.
Зная, что (cos t)’ = — sin t, (sin t)’ = cos t (подробный вывод приведен тут и тут), получаем следующую формулу:

Выводов достаточно, чтобы написать вторую функцию нахождения длины дуги эллипса.
Результат при dt = 0.001 равен 40 007 859,543 за 109 милисекунд. Отлично!
Длина дуги через эксцентриситет
Это еще не окончательный вид уравнения. В ряде интересных параметров для эллипса есть такая числовая характеристика, показывающая степень отклонения эллипса от окружности, как эксцентриситет. Формула для эллипса:

Чем эксцентриситет ближе к нулю, т.е. разница между a и b меньше, тем больше эллипс похож на окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Выразим b 2 = a 2 (1 — e 2 ), подставим в формулу (5), помним, что sin 2 t + cos 2 t = 1 (справочник [1]), убираем a 2 за знак корня, и, как постоянную величину, за знак интеграла тоже, получаем:

Пишем функцию, ожидаем более шустрого выполнения:
Результат 40 007 859.543, за чуть меньшее время, 94 милисекунды.
Длина дуги через эксцентриситет с подготовкой
Возьмем за основу последнюю функцию. Алгоритм построен так, что в цикле идем от стартового угла, к конечному, на каждой итерации подсчитывая параметр. А если сразу посчитать начальный и конечный параметры и определить условие выхода из цикла? Этим мы однозначно снизим вычислительную нагрузку внутри цикла.

То есть, вместо того, чтобы идти из точки A в точку B, мы заранее считаем параметры t1 и t2. И в цикле больше нахождением параметров не занимаемся, а только считаем очередное приращение.
Берем код последней реализации и улучшаем:
Результат — 40 007 859,543 за 30 милисекунд! Мысль явно здравая.
Длина дуги и хорошо забытые хорды
Но вернемся к сумме хорд. Что там-то не так? Казалось бы, все просто, понятно и должно работать, но результат, мягко говоря, не точен.
Работая с вещественными типами, результат зависит от «мелкости» приращения, от разрядности используемых типов. Накапливаемые погрешности, неточное представление дробного числа и прочие прелести чисел с плавающей запятой.
Тип Extended – самый точный из существующих в Delphi (и, как следствие, самый медленный). Перепишем нахождение длины дуги хордами, используя этот тип, и без вызовов внешних функций нахождения координат на эллипсе.
Результат 40 007 859.542 за 94 милисекунды. Разница в одну тысячную, и такое же время. Весьма неплохо!
Практика
Качаем, запускаем. Видим такое окно:

При запуске в полях полуосей находятся «земные» значения. Эллипс сильно смахивает на окружность. Можно сразу нажать «Расчет», увидеть значения полярного меридиана, и начинать уже эксперименты.
Для начала проверим корректность получаемых результатов. Я попытался найти какие-нибудь онлайн калькуляторы для подсчета длины дуги эллипса, в которых можно было бы указать стартовый угол и произвольное отклонение, либо просто пару углов, определяющих дугу. Но все калькуляторы считают периметр эллипса. А с произвольной дугой как-то… не встретились.
Картинка из вики:

Заскриним несколько моментов и посчитаем корректность:

Введем a=2, b=0.5, стартовый угол равен 0, отклонение θ=5.642.

Видим результат у всех один 8.055. Т.е правы все.
Аналогично поступаем с остальными тремя скринами:
- отклонение θ=1.154. У нас получился результат 1.333. На скрине видим результат s=1.334. Как так? Давайте увеличим «Дельту» в 10 раз, т.е. вместо 0.001, сделаем 0,01. У всех интегральных 2) 3) 4) результат станет 1.334. В то время, как у 1) и 5), т.е. примитивно-неинтегрально-хордовых останется 1.333.
Какой результат более истинный? Смотрите сами. Уменьшение дельты, т.е. угла для подсчетов, ведет к более точному результату. На 0.001 интегральные функции выдали результат как хордовые. При более грубой дельте, интегральные чуть изменились, а хордовые верны своему результату.
Сделаем дельту очень мелкой, равной 0.00001. Результат у всех, кроме первой, тот же, 1.333.
Лично я начинаю верить 5-ой формуле.
- отклонение θ= 206. У нас получился результат 4.322. На скрине результат s= 4.322. Дельта 0.001. Все отлично.
- отклонение θ= 4,488. У нас получился результат 5,989. На скрине результат s= 5,989. Дельта 0.001. Все отлично.
Вывод : Формулы 2-5 работают как надо. Фаворит 5. За меньшее время, т.е. при более «грубой» дельте, находит правильный результат.
Проверим на ужасных эллипсах. Т.е. где эксцентриситет очень близок к единице.

Можем заметить следующее: при 0.00001 функции 2 и 3 дали результат, близкий к результату функции 4, полученный при дельте 0.001. При дельте 0.00001 функция 4 дала результат, близкий к результату функции 5. Сама же функция 5 слабо колеблется в показаниях, что при дельте в 0.001, что при 0.00001.
Аналогичную ситуацию можно пронаблюдать при сильно вытянутом эллипсе:

Таким образом, имеет смысл использовать функции 4 и 5. Одну, как представительницу интегрального сословия, самую быструю и более точную из них. Другую, как представительницу очевидного и простого метода, работающую, между тем, лучше своих интегральных коллег при минимальных ресурсных затратах.
Небольшая инструкция
Правая кнопка мыши задает стартовый угол. Удерживая правую кнопку мыши можно «прогуляться» по эллипсу. Конечная точка дуги будет следовать за стартовой точкой, отстоя на заданный ранее угол. Если поставить галку на «сохранять параметрическое отклонение», параметрический угол между t1 и t2 станет неизменен. Очень полезно пронаблюдать, как будет меняться сектор.
Левая кнопка мыши задает конечную точку дуги, т.е. угол отклонения.
Скачать
Друзья, спасибо за внимание!
Периметр эллипса. Точный онлайн расчет
| Значения полуосей эллипса |
| Большая полуось a |
| Малая полуось b |
| Уравнение эллипса | ||||
| Эксцентриситет эллипса | ||||
| Точный периметр эллипса | ||||
Расчет длины/периметра эллипса совсем не является тривиальной задачей, как можно было бы подумать. Легко рассчитать длину окружности, по формуле Но такой же простой подход совершенно не подходит для эллипса. В точном выражении периметр эллипса можно выразить только через эллиптические функции вот по такой формуле — большая полуось эллипса В быту, конечно же используются приближеные формулы, о которых мы расскажем. Одна из них выглядит вот так В два раза более точные данные дает формула И еще более точный периметр эллипса дает выражение Но, все равно каковы бы не были формулы, они все равно только приближенно дают периметр эллипса. Мы, с помощью точной формулы через эллиптический интеграл, получаем независимость от подобных ограничений, и получаем абсолютную точность, при любых значениях эллипса. Решение примеровЭллипс задан уравнением Найти его периметр Введем известные параметры a=2 и b=5 и получим результат
|