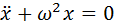Найти фазовый поток дифференциального уравнения

Векторное поле $\xi$ на многообразии $M$ (или на какой-либо области в $M$) определяется заданием в каждой точке $x$ касательного вектора $\xi(x)\in T_xM$ так, что его координаты $\xi_i(x)$ являются дифференцируемыми функциями от локальных координат точки.

Аналогично, внешняя дифференциальная форма $\omega$ на $M$ (или на какой-либо области в $M$) определяется заданием в каждой точке $x$ кососимметрической полилинейной функции $\omega_x$ на $T_xM\times\dots\times T_xM$. В локальных координатах можно записать $$\omega=\sum_Симплектическое многообразие — это многообразие $M$, в каждой точке которого на касательном пространстве $T_xM$ задана невырожденная кососимметрическая билинейная форма (кососкалярное умножение) $\omega_x(\xi,\eta)=\sum_\omega_(x)\xi_i\eta_j$, причём функции $\omega_$ дифференцируемы, и возникающая на $M$ симплектическая 2-форма $$\omega=\sum_^<2l>$ со стандартной симплектической формой $$\omega=dx_1\wedge dy_1+\dots+dx_l\wedge dy_l,$$ где $x_1,\dots,x_l,y_1,\dots,y_l$ — координаты на $\mathbb^<2l>$.

Кроме стандартного примера $M=\mathbb^<2l>$, простейшими примерами симплектических многообразий являются двумерные ориентируемые поверхности с 2-формой площади, задающей ориентацию (условие замкнутости здесь выполнено по соображениям размерности). Например $M=\mathbb^2$ с обычной формой площади ($\omega(\xi,\eta)$ — площадь ориентированного параллелограмма, натянутого на векторы $\xi,\eta$) — частный случай стандартного примера. Ещё пример: $M=S^2$ с формой площади $\omega(\xi,\eta)=(\xi,\eta,\nu)$ (смешанное произведение), где $\nu$ — вектор внешней нормали к сфере в данной точке.

Далее будут рассмотрены более общие естественные классы симплектических многообразий.

Задача 22.1. $L_<\xi>\eta=[\xi,\eta]$ для любых векторных полей $\xi,\eta$.

Задача 22.2. Значение дифференциала внешней формы $\omega$ степени $m$ на наборе векторных полей $\xi_0,\xi_1,\dots,\xi_m$ может быть вычислено по формуле \begin d\omega(\xi_0,\xi_1,\dots,\xi_m)=\sum_i(-1)^i\partial_<\xi_i>\omega(\xi_0,\dots,\,\not\!\xi_i,\dots,\xi_m)-<>\\<>— \sum_Внутреннее произведение внешней формы $\omega$ степени $m$ и векторного поля $\xi$ — это внешняя форма $i_<\xi>\omega$ степени $m-1$, получаемая подстановкой $\xi$ в $\omega$ в качестве одного из аргументов: $$ i_<\xi>\omega(\xi_1,\dots,\xi_)=\omega(\xi,\xi_1,\dots,\xi_). $$ Операции внутреннего умножения, внешнего дифференциала и производной Ли дифференциальных форм связаны формулой гомотопии: $$ L_<\xi>\omega=-d(i_<\xi>\omega)-i_<\xi>(d\omega). $$

Фазовые портреты «на пальцах» или что можно узнать о решениях диффура, не решая его

Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?

Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.

Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.

Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:

Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.

Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:

Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:

Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.

Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):

Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:

По горизонтальной оси отложена величина x, по вертикальной — u

Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.

По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).

Следует однако помнить, что замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому мы не можем доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырех приведенных траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку x это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение стержня, то есть правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.

Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:

В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.

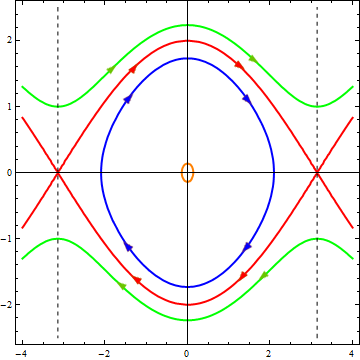
По горизонтальной оси отложена величина x, по вертикальной — u

Как видите, процессы происходящее в системе стали более разнообразными:

При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.

При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.

При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.

А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:

По горизонтальной оси отложено время, по вертикальной — x

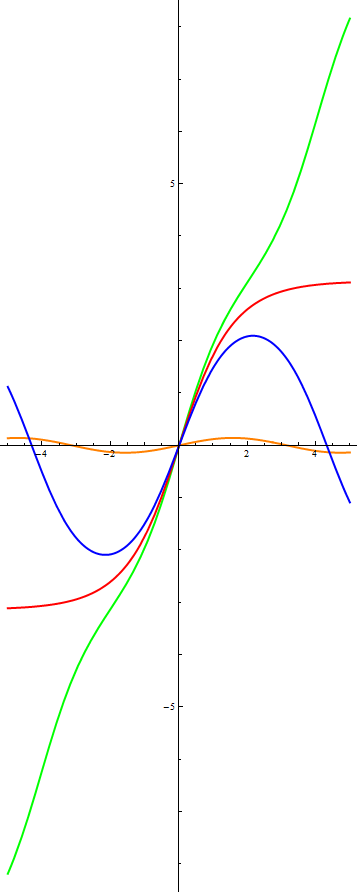
По горизонтальной оси отложено время, по вертикальной — x

Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.

Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.

Модуль 1. Принцип динамического расширения—сжатия фазового пространства в теории управления

1.5. Принцип динамического расширения—сжатия фазового пространства

В соответствии с теорией АКАР законы управления (1.2) обеспечивают обязательный перевод ИТ системы (1.1) из произвольного начального состояния в окрестность заданного многообразия $\psi=0$ (1.3) или пересечения многообразий $\psi_s=0$ (1.11). Размерность подпространства этих многообразий, куда попадет ИТ в результате действия указанных законов управления, равна $n-1$ — для скалярного или $n-m$ — для векторного управлений соответственно. Выше была установлена тесная связь многообразий (1.3) и (1.11) с инвариантными соотношениями в механике, технике и вообще в естествознании.

Возникает важный вопрос о направлении и свойствах дальнейшего движения ИТ вдоль указанных многообразий под действием синтезируемых управлений. Другими словами, необходимо разработать общий принцип такого деформирования фазового пространства динамической системы под действием внутренних управлений, при котором ИТ могла бы пройти “вглубь” подпространства многообразий (1.3) или (1.11) с последующим попаданием в начало координат или на заданное финишное многообразие согласно основной задаче управления.

В предыдущих разделах уже обсуждалась постановка основной задачи синтеза замкнутой системы, которая в общем виде обычно ставится как определение такого закона управления в функции координат состояния, который переводит изображающую точку (ИТ) объекта $n$-го порядка из произвольного начального состояния $x_<10>,i=1,\dots,n$ в заданное конечное состояние, например в начало координат фазового пространства.

Подчеркнем тот очевидный факт, на который почему-то редко обращают внимание, что в начальный момент $t=0$ ИТ находится в пространстве размерности $n$, в конечный же момент, т.е. после завершения процесса управления, ИТ попадает в точку $\mathbf x_k(0,\dots,0)$ с нулевой размерностью. Это означает, что под действием управления ИТ постепенно переходит из исходного пространства размерности $n$ в подпространство размерности $n-1$, затем $n-2$, $n-3$ и т.д. вплоть до одномерного многообразия $\dim(\psi_s)=1$, двигаясь вдоль которого на финишном участке ИТ и попадает в начало координат фазового пространства. Другими словами, под действием непрерывного управления происходит постепенное сжатие объема фазового потока, в котором движется ИТ объекта.

1.5.1. Фазовый поток в диссипативных системах

Строгое определение понятия фазового потока приведено в [38, 39]. Пусть для динамической системы $M$ — фазовое пространство детерминированного процесса, тогда точка этого пространства представляет определенное состояние процесса. Если в момент $t=0$ процесс был в состоянии $\mathbf x$, то в другой момент состояние процесса будет уже $\mathbf G^t\mathbf x$ (где $\mathbf G^t$ — однопараметрическая группа преобразований за время $t$), т.е. для каждого $t$ определено отображение $\mathbf G^t:M\to M$ фазового пространства процесса в себя. Именно однопараметрическая группа преобразований множества $M$ и называется фазовым потоком с фазовым пространством $M$. В физическом плане можно, например, представить себе фазовое пространство заполненным жидкостью, тогда частица $\mathbf x$ через время $t$ переходит в точку $\mathbf G^t\mathbf x$, а орбиты фазового потока являются фазовыми траекториями. Под действием фазового потока ИТ движется так, что вектор скорости системы в каждый момент времени равен вектору фазовой скорости в той точке фазового пространства, где находится ИТ системы. Поэтому фазовым потоком векторного дифференциального уравнения
$$
\dot <\mathbf x>(t)=\mathbf
$$ называется однопараметрическая группа диффеоморфизмов (гладких преобразований), для которой $\mathbf F$ является векторным полем фазовой скорости. Для того, чтобы найти фазовый поток дифференциального уравнения, достаточно решить это уравнение [38, 39]. Напомнив эти фундаментальные понятия современной теории дифференциальных уравнений, вернемся к явлению сжатия фазового объема в системах управления.

Предположим теперь, что синтезирован закон разрывного, например кусочно-непрерывного, управления объектом. В этом случае очевидно, что указанное сжатие фазового объема будет происходить скачком в определенные моменты времени. В качестве примера, подтверждающего это положение, рассмотрим задачу синтеза законов оптимального по быстродействию управления. Дело в том, что теория оптимального по критерию быстродействия управления в концептуальном плане является вершиной в современной теории автоматического управления по сравнению с любыми другими критериями качества. С одной стороны, оптимальное по быстродействию управление непосредственно отражает динамическую парадигму естествознания, основанную на пространственно-временном подходе, а с другой стороны, известно, что к задаче быстродействия может быть сведена задача оптимизации системы по любому другому критерию, отличному от критерия быстродействия. Указанная процедура сведения осуществляется путем расширения фазового пространства исходной системы на одну дополнительную координату, равную соответствующему критерию качества. Предположим, что объект является неосциллирующим и описывается дифференциальными уравнениями
$$
\dot x_1(t)=x_2, \quad \dot x_2(t)=u, \quad |u|\le u_<\max>.\qquad
(1.18)$$Известно [40], что закон оптимального по быстродействию управления объектом (1.18) имеет следующий вид:
$$
u(x_1,x_2)=-u_<\max>\mathrm\,\mu(x_1,x_2)=-u_<\max>\mathrm\left(x_1 + \frac<0,5>>x_2|x_2|\right).\qquad
(1.19)$$Закон (1.19) обеспечивает двухинтервальное управление $\pm u$ по переводу ИТ из произвольного начального состояния $(x_<10>,x_<20>)$ в начало координат (0,0) фазовой плоскости (рис. 1.1). При этом на первом интервале ИТ движется по полутраектории, имеющей размерность $\dim x=2$, однако в момент переключения $t=t_1$ знака управления происходит сжатие площади фазового потока. Далее ИТ будет двигаться теоретически по линии переключения $\mu(x_1,x_2)=0$, имеющей размерность, равную уже $\dim \mu=1$. Покажем, что это действительно так. Уравнение линии переключения согласно (1.19) имеет вид

$$
\mu(x_1,x_2)=x_1+ \frac<0,5>>x_2|x_2|=0.\qquad
(1.20)$$ Тогда с учетом первого уравнения объекта (1.18) из (1.20) получим
$$
\dot x_1(t)|\dot x_1(t)| + 2u_<\max>x_1(t)=0\qquad
(1.21)$$ или
$$
\dot x_2(t) + u_<\max>\mathrm x_2(t)=0.\qquad
(1.22)$$Дифференциальные уравнения (1.21) или (1.22>, описывающие движение ИТ вдоль линии переключения (1.20) относительно $x_1(t)$ или $x_2(t)$ соответственно, имеют уже размерность $\dim \mu=1$, хотя исходный объект имел $\dim \mathbf x=2$. Итак, на линии переключения (1.20) произошло сжатие фазового объема, а ИТ, двигаясь вдоль этой линии, в момент $t=t_2$ прибывает в начало координат $\dim \mathbf O=0$ фазовой плоскости замкнутой системы (1.18), (1.19). Подчеркнем, что сжатие площади фазового потока происходит скачком в момент переключения управления и попадания ИТ на линию переключения.

Рис. 1.1. Фазовый портрет оптимальной по быстродействию системы 2-го порядка

Рис. 1.2. Фазовый портрет оптимальной по быстродействию системы 3-го порядка

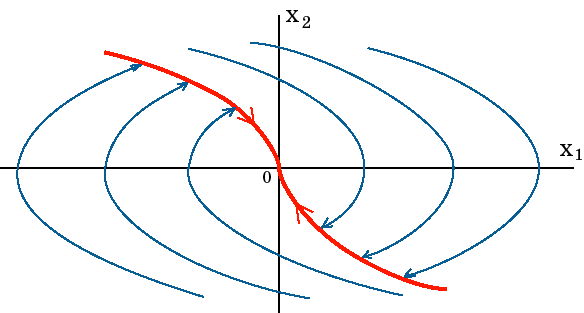
Аналогичная картина движения ИТ имеет место и при оптимальном по быстродействию трехинтервальном управлении $\pm u_<\max>$ неосциллирующими объектами третьего порядка (рис. 1.2). В этом случае ИТ движется на первом интервале по полутраектории $\mathbf_0 \mathbf _1$, стартуя, например, из точки $\mathbf N_0$, находящейся в трехмерном пространстве $\dim \mathbf x=3$. В момент первого переключения $t=t_1$ управления ИТ попадает в точке $\mathbf N_1$ на двумерную $\dim \mathrm L_2=2$ поверхность переключения $ \mathrm L_2$, при этом происходит первое сжатие объема фазового потока. Далее, двигаясь вдоль $ \mathrm L_2$, ИТ в момент второго переключения $t=t_2$ попадает в точке $\mathrm N_1$ на одномерную $\dim \mathrm L_1=1$ линию $\mathrm L_1$, являющуюся “краем” поверхности переключения $\mathrm L_2$, при этом происходит второе сжатие фазового объема. Затем, двигаясь по линии $\mathrm L_1$, ИТ в момент $t=t_3$ обязательно попадает в начало координат, имеющее нулевую размерность.

Итак, в рассмотренном оптимальном по быстродействию процессе (рис. 1.2) происходит скачкообразное $\pm u_<\max>$ трехкратное сжатие фазового объема, в результате чего ИТ, начиная свое движение из точки, находящейся в исходном трехмерном пространстве, попадает в начало координат фазового пространства с нулевой размерностью. В связи с тем, что в течение оптимального процесса знаки управляющего воздействия $\pm u_<\max>$ чередуются на соседних интервалах, то концы множества фазовых полутраекторий предпоследнего интервала $ \mathrm L_2^-$ (рис. 1.2) будут принадлежать полутраектории $\mathrm L_1^+$ и, следовательно, концы полутраектории $ \mathrm L_2^+$ будут принадлежать полутраектории $\mathrm L_1^-$. В своей совокупности полутраектории второго интервала $ \mathrm L_2^+$ и $ \mathrm L_2^-$ образуют две двумерные поверхности, которые стыкуются по одномерной линии $\mathrm L_1$. Эти поверхности, имеющие в качестве края линию $\mathrm L_1$, образуют в целом поверхность переключения $\mathrm L_2$, двигаясь вдоль которой ИТ попадает на линию $\mathrm L_1$ и далее в начало координат. Это означает, что, попав в момент $t=t_1$ на двумерную поверхность $\mathrm L_2$, ИТ будет находиться на ней в течение двух последних интервалов вплоть до окончания в момент $t=t_3$ оптимального по быстродействию процесса [28, 40].

Аналогичным образом происходит процесс сжатия фазового объема при оптимальном по быстродействию управлении объектами более высокого $(n>3)$ порядка. В этом случае, продолжая предыдущие рассуждения, нетрудно показать, что полутраектории $\mathrm L_3^+$ и $\mathrm L_3^-$, концы которых соответственно располагаются на поверхностях $\mathrm L_2^+$ и $\mathrm L_2^-$, образуют в своей совокупности трехмерное многообразие $\mathrm L_3$. Далее, продолжая указанное построение, последовательно получим многообразия $\mathrm L_4,\mathrm L_5,\dots,\mathrm L_,\mathrm L_n$. Отсюда непосредственно следует, что каждое многообразие $\mathrm L_k$, в свою очередь, принадлежит многообразию $\mathrm L_$ и разбивает его на две области $\mathrm L_^+$ и $\mathrm L_^-$, а все полутраектории из семейства $\mathrm L_^+$ заканчиваются на $\mathrm L_^-$ и, следовательно, все полутраектории $\mathrm L_^-$ заканчиваются на многообразии $\mathrm L_$. Очевидно, что для неосциллирующих объектов задача синтеза в конечном итоге сводится к поиску непроницаемого многообразия $\mathrm L_$, разбивающего фазовое пространство $\mathrm L_$ на две области, в одной из которых $u(t)=+u_<\max>$, а в другой $u(t)=-u_<\max>$. При этом многообразие $\mathrm L_$ включает в себя многообразия $\mathrm L_,\mathrm L_,\dots,\mathrm L_2$, и, наконец, одномерную линию $\mathrm L_1$, двигаясь по которой ИТ попадает на многообразие $\mathrm L_0$, состоящее из единственной точки (начала координат) и имеющее нулевую размерность.

Итак, начав движение в исходном фазовом пространстве $\mathrm L_n$, ИТ в результате первого переключения знака управления сначала попадает на многообразие $\mathrm L_(\dim \mathrm L_=n-1)$, например $\mathrm L_^-$, двигаясь по которому она попадет на многообразие $\mathrm L_^+$, затем на $\mathrm L_$, $\mathrm L_$ и т.д. В конечном итоге ИТ попадает на двумерную поверхность $\mathrm L_2$ и после последнего переключения знака управления $t=t_$ она по одномерной линии $\mathrm L_1$ приходит в начало координат фазового пространства.

Подчеркнем, что при оптимальном по быстродействию процессе ИТ последовательно переходит от одного многообразия $k$-ой размерности $(\dim \mathrm L_k=k)$ к следующему многообразию $(k-1)$-ой размерности $(\dim \mathrm L_=k-1)$, при этом сжатие фазового объема происходит в точках переключения знака управляющего воздействия.

Разумеется, что описанная выше картина движения ИТ в фазовом пространстве является в определенной мере математической идеализацией, т.к. в реальных условиях переключение управления с одного знака $(+u_<\max>)$ на другой $(-u_<\max>)$ происходит не мгновенно, а за определенное время, кроме того, могут существовать неучтенные малые запаздывания и т.д. В результате при реальном оптимальном по быстродействию управлении ИТ будет двигаться не абсолютно точно по соответствующей гиперповерхности переключения $\mathrm L_k$, а в некоторой ее окрестности, т.е. в некотором “пограничном слое”, находящемся в сжимающемся фазовом потоке. Однако описанная выше картина движения ИТ при идеальном оптимальном по быстродействию процессе позволяет четко и наглядно выявить такое фундаментальное свойство, как эффект сжатия объема фазового потока при переходе ИТ с одного многообразия на другое подмногообразие пониженной размерности вплоть до попадания в начало координат фазового пространства замкнутой системы. В этом эффекте как раз и состоит, помимо прочих достоинств, одна из замечательных, концептуальных особенностей оптимальных по быстродействию систем. Очевидно, что выявленный эффект сжатия фазавого объема имеет весьма важное общетеоретическое значение для проблемы синтеза систем управления.

Рассмотренный процесс сжатия фазового объема в оптимальных по быстродействию системах, когда ИТ попадает и затем движется по многообразиям последовательно понижающейся размерности $\mathrm L_,\mathrm L_,\dots,\mathrm L_1,\mathrm L_0$, может быть интерпретирован как процесс попадания и движения ИТ вдоль желаемого оптимального многообразия, обладающего свойством минимальности времени движения. В этом случае желаемое многообразие $\psi=0$ не задается каким-либо произвольным образом, а находится в результате строгой процедуры синтеза гиперповерхности переключения. Аналогичное положение имеет место и при оптимизации систем не по быстродействию, а по другим критериям качества. Это означает, что в оптимальных системах применение метода АКАР связано с выявлением оптимальных многообразий, входящих в соответствующие законы управления. При этом определяющее значение для поиска многообразий имеет заданный критерий оптимальности синтезируемой системы.

Описанные выше и представленные на рис. 1.1 и рис. 1.2 процессы сжатия фазового потока происходили в оптимальных по быстродействию системах, являющихся исходно нелинейными. Но оказывается, что сходные явления наблюдаются и в линейных системах, свойства которых, как известно, существенно зависят от корней характеристического уравнения $\lambda_1$. В этой связи рассмотрим линейную систему в трехмерном фазовом пространстве и воспользуемся замечательными графическими иллюстрациями из работы [38]. В этом случае характеристическое уравнение представляет собой вещественное кубическое уравнение, которое может иметь три вещественных корня или один вещественный и два комплексных. Решение линейного дифференциального уравнения третьего порядка, как известно, имеет следующий вид:
$$
x(t)=C_1\exp(\lambda_1 t) \xi_1 +C_2\exp(\lambda_2 t) \xi_2 + C_1\exp(\lambda_3 t) \xi_3,\qquad
(1.23)$$где $\xi$ — какой-нибудь собственный вектор с собственными значениями $\lambda_k$, $k=1,2,3$. Выберем эти значения вещественными, тогда с учетом того, что $\exp(\lambda t)$, $(\mathrm \lambda 0$) в одном направлении и одновременно сжимается (как $\exp(-\lambda\cdot t)$, $\lambda>0$) в перпендикулярном ему направлении. Но так как $\exp(\lambda\cdot t)\cdot \exp(-\lambda\cdot t)\equiv1$, то площадь или объем во втором случае также сохраняются [41]. В динамическом отношении в первом случае траектории движения устойчивы, а во втором — неустойчивы.

Для консервативных систем характерна инвариантность их свойств относительно обращения времени, что свидетельствует о сохранении их энергии. В диссипативных же системах обращение времени приводит к кардинальному изменению их свойств, в частности, к эффекту сжатия их фазового объема, что указывает на рассеивание энергии. Диссипативные системы могут обладать весьма многообразными режимами, в особенности когда их динамика включает в себя как эффекты затухания, так и механизмы, поддерживающие их движение, при этом объем этих систем в фазовом пространстве всегда не сохраняется, а динамика необратима. Другими словами, диссипативным системам обязательно присуще свойство сжатия площадей или объемов в фазовом потоке. Однако это вовсе не означает, что в этих системах невозможно расхождение, т.е. неустойчивость траекторий движения. В действительности в них могут возникать режимы, когда сокращение площадей или объемов достигается не только за счет сокращения всех длин, а в результате существенного сокращения одних длин при менее быстром сокращении других.

Иначе говоря, при общем сокращении площадей или объемов в фазовом пространстве диссипативных систем по некоторым направлениям их траектории могут разбегаться и движение по этим направлениям будет неустойчивым. Свойство разбегания траекторий объясняется необратимостью процессов, при этом сжимающийся и растягивающийся слои фазового потока будут соответствовать двум реализациям динамики, каждая из которых отражает эффект нарушения временной симметрии и парное появление несимметричных режимов. В этом случае сжимающийся слой в фазовом пространстве отвечает состоянию системы в будущем, а растягивающийся — в прошлом, т.е. налицо две реализации с противоположной ориентацией по времени [42].

Ранее уже отмечалось, что второе начало термодинамики, как принцип отбора, допускает только те начальные условия, в которых система эволюционирует к будущему равновесному состоянию. Эти качественные особенности диссипативных систем обязательно следует учитывать при разработке методов синтеза замкнутых нелинейных систем.

1.5.2. Аттракторы и сжатие фазового объема

Нелинейные диссипативные динамические системы обладают свойством притяжения траекторий, проходящих через определенную область фазового пространства, к некоторому многообразию, называемому аттрактором. По определению [41], аттрактором $\mathrm A$ называется некоторое компактное множество в фазовом пространстве, имеющее следующие основные свойства:

во-первых, аттрактор $\mathrm A$ инвариантен относительно действия фазового потока, т.е. $\mathrm$;

во-вторых, аттрактор имеет нулевой объем в $n$-мерном фазовом пространстве динамической системы;

в-третьих, аттрактор находится в некоторой области ненулевого объема, которая является областью притяжения данного аттрактора, т.е. в фазовом пространстве системы существует некоторое множество таких точек, что выходящие из них траектории при $t\to\infty$ всегда устремляются к аттрактору.

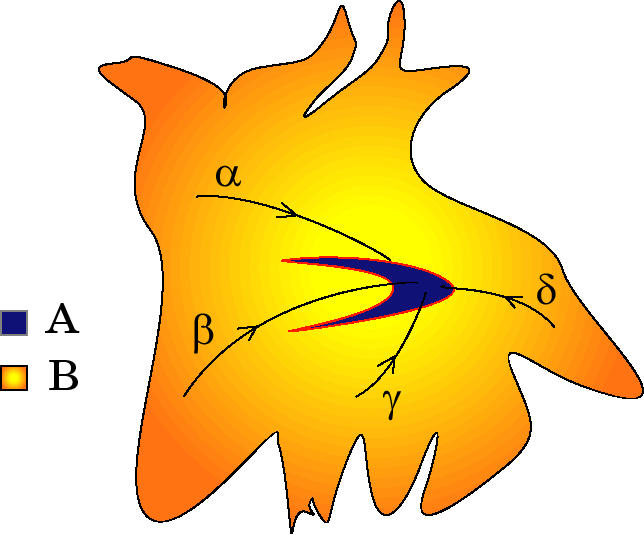
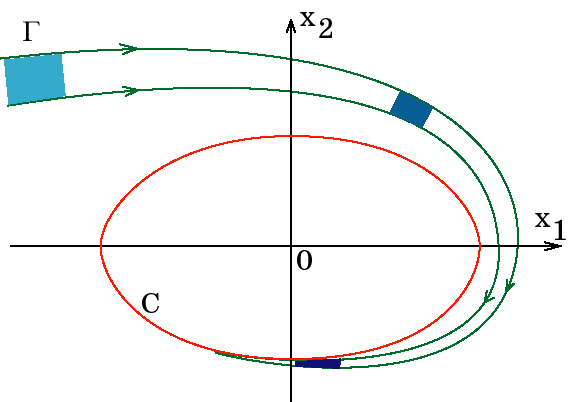
На рис. 1.8, взятом из [41], схематически изображен аттрактор $\mathrm A$ и его область притяжения $\mathrm B$. Траектории, выходящие из точек $\alpha$, $\beta$, $\gamma$ и $\delta$, переносятся фазовым потоком $\Phi$ к аттрактору. В математическом плане аттрактор представляет собой асимптотический предел решений дифференциальных уравнений нелинейной диссипативной системы, причем начальные условия этих решений должны обязательно лежать в области притяжения.

Для того, чтобы нагляднее показать особенности, возникающие при сжатии фазового объема, рассмотрим, следуя [41], фазовый портрет нелинейной диссипативной системы второго порядка с аттрактором в виде предельного цикла. Для этого предположим, что множество начальных условий на фазовой плоскости, откуда стартует ИТ, занимает некоторую область $\Gamma$ (рис. 1.9). В результате диссипации фазовый поток приводит к сокращению площади $\Gamma$ по мере движения ИТ до некоторого линейного отрезка на аттракторе $\mathrm C$ — предельном цикле, имеющем размерность $\dim \mathrm C$. Это означает, что происходит потеря информации относительно взаимного расположения исходных начальных условий в области $\Gamma$ фазовой плоскости. После достижения ИТ аттрактора $\mathrm C$ информация об исходных начальных условиях полностью утрачивается, что является следствием эффекта сжатия площади фазового потока и наличия аттрактора системы. Учитывая, что никаких особенностей у рассматриваемой системы, кроме наличия аттрактора, не предполагалось, то этот факт означает справедливость указанного свойства для любого другого типа аттрактора, а именно: свойства потери информации о начальных условиях старта ИТ системы.

Рис. 1.8. Аттрактор и его область притяжения

Рис. 2.9. Иллюстрация сокращения площадей в фазовом пространстве

Аналогичные свойства будут присущи и нелинейным системам третьего порядка, имеющим аттрактор в виде некоторого двумерного тора в трехмерном фазовом пространстве. Изображенные на рис. 1.8 и рис. 1.9 аттракторы лежат на некоторых многообразиях и сами образуют многообразия в фазовом пространстве системы. В частности, предельный цикл является простым многообразием, что предполагает наличие касательной в каждой его точке. Изложенные свойства аттракторов позволяют сделать общий важный вывод: размерность $(m)$ аттрактора всегда меньше размерности $(n)$ фазового пространства исходной динамической системы, т.е. $m 0.
$$

Отсюда непосредственно следует, что при $t\to\infty$ объем $V\to 0$, т.е. объем (площадь) самого аттрактора всегда равен нулю. Это важный и нетривиальный вывод, следующий из свойства сжатия фазового потока в диссипативных системах.

Таким образом, к важнейшим для метода АКАР свойствам диссипативных нелинейных систем относятся, во-первых, “потеря” ими памяти о начальных условиях, откуда начинает свое движение ИТ системы, и, во-вторых, обязательное снижение размерности аттрактора по сравнению с размерностью фазового пространства исходной системы.

В последнее время исследование динамики нелинейных диссипативных систем привело к открытию так называемых “странных аттракторов” с весьма своеобразными свойствами. Дело в том, что в обычных динамических системах вследствие детерминистского подхода к их изучению фазовые траектории принципиально не должны пересекаться в фазовом пространстве. В противном случае одно начальное условие могло бы породить разные фазовые траектории, т.е. система после точки пересечения траекторий могла вести себя совершенно по-разному, а ее поведение оказалось бы совершенно непредсказуемым. Именно эта базовая установка лежит в основе известной детерминистской доктрины, согласно которой в детерминированных динамических системах невозможно хаотическое поведение. Однако в действительности оказалось, что в фазовом пространстве нелинейных детерминированных систем, имеющих размерность три и выше, при определенных видах нелинейностей и сочетании параметров принципиально могут существовать аттракторы, обладающие весьма необычными свойствами, а именно: близкие траектории, попавшие на такой аттрактор, начинают быстро расходиться. В результате на аттракторе возникает хаотический режим движения, отличительным свойством которого является чрезвычайная чувствительность к заданию начальных условий, находящихся на аттракторе. Внешне же фазовые траектории, имеющие начальные условия вне аттрактора, стремятся к аттрактору и “оседают” на нем. Но самой удивительной особенностью этих аттракторов является их нецелая размерность (например, $2 1$) сначала осуществляется параллельное введение совокупности $m$ первых интегралов, т.е.
$$
\psi_1(x_1,\dots,x_n)=0,\dots,\psi_m(x_1,\dots,x_n)=0.
$$Затем на пересечении этих многообразий осуществляется аналогично скалярному управлению последовательное вложение $r$ первых интегралов друг в друга, т.е.
$$
\begin
&\psi_(x_1,\dots,x_)=0 \to \psi_(\psi_,x_1,\dots,x_)=0 \to \dots\\
&\to\psi_r(\psi_,\dots,\psi_,x_1,\dots,x_)=0, \quad r\le n-m-1.
\end
$$Другими словами, при последовательном $(m=1)$ введении $s$ первых интегралов образуется один общий первый интеграл $\psi_s=0$, а при параллельно-последовательном ($m>1$) введении образуется $m$ первых интегралов будущей замкнутой динамической системы. Для реализации изложенного процесса сжатия фазового объема необходимо соответствующим образом синтезировать законы управления. Именно эти управления вводят в замкнутую систему соответствующую энергию, в результате чего происходит изменение состояния системы, которое проявляется в изменении градиентов $\left(\dfrac