Особые решения дифференциальных уравнений
Решение дифференциального уравнения
называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению
Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).
Полученное после исключения из (1) и (2) уравнение
Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.
Пример 1. Найти особые решения дифференциального уравнения
а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем
Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.
б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).
в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение
Выпишем условие касания двух кривых и в точке с абсциссой :
Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .
Полагая , находим, что условия (7) принимают вид
Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.
Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).
г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).
Огибающей семейства кривых
называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.
Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.
Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.
Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений
Некоторая ветвь СДК заведомо будет огибающей, если на ней:
1) существуют ограниченные по модулю частные производные
где и — постоянные;
Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.
Пример 2. Найти особые решения дифференциального уравнения
а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда
Это и есть C-дискриминантная кривая: она состоит из двух прямых и .
б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).
в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке
где — область допустимых значений .
Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).
Итак, установлено, что каждое из решений (15) есть особое решение.
В вопросах отыскания особых решений оказываются полезными следующие символические схемы:
Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места точек заострения (возврата);
3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.
Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;
3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.
Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).
Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.
В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.
Пример 3. Найти особое решение дифференциального уравнения
Решение. Особое решение, если оно существует, определяется системой
где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви
Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).
Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства
являющегося общим интегралом для (18).
Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.
Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).
Пример 4. Найти особые решения дифференциального уравнения
Решение. Дифференцируем (23) по
Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.
Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).
Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).
Пример 5. Найти особые решения дифференциального уравнения
Решение. Найдем . Исключая из системы уравнений получаем
Преобразовав уравнение (25) к виду , находим его общий интеграл .
Найдем . Исключая из системы уравнений будем иметь
Итак, из (26) и (27) имеем
Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.
Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .
Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).
Пример 6. Найти особые решения дифференциального уравнения
а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда
Подставляя (29) в (28), найдем уравнение :
б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде
Дифференцируя обе части (28) по и учитывая, что , будем иметь
Приравнивая нулю первый множитель , получаем (29), а соотношение дает
Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):
в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь
Подставляя (34) в (33), получаем уравнение .
Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).
Особые точки кривой
Понятие частной производной используется при исследовании кривых.
Пусть кривая задана уравнением
Угловой коэффициент касательной к кривой определяется по формуле
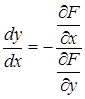
Если в данной точке М(х, у) рассматриваемой кривой по крайней мере одна из частных производных 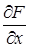
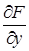
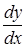
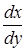
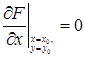
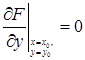
то угловой коэффициент касательной становится неопределенным.
Определение. Если в точке М0(х0, у0) кривой F(х, у) = 0 обе частные производные 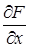
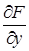
F = 0, 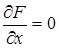
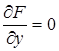
Естественно, что не всякая кривая имеет особые точки. Так, например, для эллипса
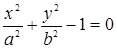
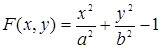
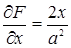
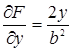
производные 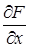
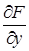
Не предпринимая подробного исследования поведения кривой вблизи особой точки, рассмотрим несколько примеров кривых, имеющих особые точки.
Пример 45. Исследовать особые точки кривой
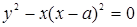
Решение. В данном случае 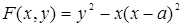
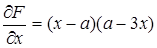
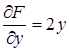
Решая совместно три уравнения
F = 0, 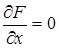
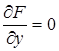
находим единственную удовлетворяющую им систему значений х и у:
Следовательно, точка М0(а, 0) есть особая точка кривой.
Исследуем поведение кривой вблизи особой точки и построим кривую. Перепишем данное уравнение в виде 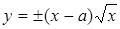
Мы рассмотрим сначала ту часть кривой, которая соответствует знаку +: 
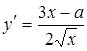
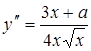
При х = 0 имеем 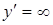
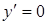
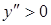
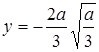
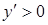
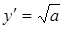

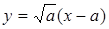
Так как вторая ветвь кривой 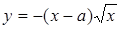
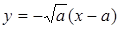
Через особую точку кривая проходит дважды. Такая точка называется узловой точкой.
Рассмотренная кривая изображена на рис. 10.
 |  |
Пример 46. Исследовать на особые точки кривую (полукубическая парабола) у 2 – х 3 = 0.
Решение. Координаты особых точек определяются из системы уравнений: у 2 – х 3 = 0, 3х 2 = 0, 2у = 0. Следовательно, М0(0, 0) есть особая точка.
Перепишем данное уравнение в виде 
Функция у определена только при х ³ 0, неотрицательна и возрастает при возрастании х.
Найдем первую и вторую производные от функции 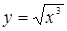
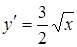
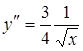
При х = 0 имеем у = 0, у¢ = 0. Следовательно, рассматриваемая ветвь кривой имеет в начале координат касательную у = 0. Вторая ветвь кривой 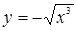
Заметим, что кривую у 2 – х 3 = 0 можно рассматривать как предельный случай кривой у 2 = х(х – а) 2 (рассмотренной в примере 45), когда а ® 0, т.е. когда петля кривой стягивается в точку.
Пример 47. Исследовать кривую (у – х 2 ) 2 – х 5 = 0.
Решение. Координаты особых точек определяются системой уравнений
которая имеет единственное решение: х = 0, у = 0. Следовательно, начало координат есть особая точка.
Перепишем данное уравнение в виде 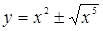
Определим производные первого и второго порядка:

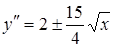
Исследуем ветви кривой, соответствующие знакам плюс и минус, в отдельности. В обоих случаях при х = 0 имеем: у = 0, у¢ = 0, т.е. для обеих ветвей оси Ох является касательной. Рассмотрим сначала ветвь 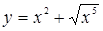
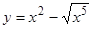
При х = 16/25 функция 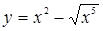
|
 |  |
|



Таким образом, в данном случае в начале координат встречаются две ветви кривой; обе ветви имеют одну и ту же касательную и расположены по одну сторону от касательной вблизи точки касания. Такая особая точка называется точкой возврата второго рода. График рассматриваемой функции изображен на рис. 12.
Пример 48. Исследовать кривую у 2 – х 4 + х 6 = 0.
Решение. Начало координат есть особая точка. Для исследования кривой вблизи этой точки перепишем уравнение кривой в виде 
Так как уравнение кривой содержит только четные степени переменных, то кривая симметрична относительно осей координат и, следовательно, достаточно исследовать часть кривой, соответствующую положительным значениям х и у. Из последнего уравнения следует, что х может изменяться на отрезке от 0 до 1, т.е. 0 £ х £ 1.
Вычислим первую производную для той ветви кривой, которая является графиком функции 
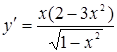
При х = 0 имеем у = 0, у¢ = 0. Следовательно, в начале координат кривая касается оси Ох.
При х = 1 имеем у = 0, у¢ = ¥; следовательно, в точке (1, 0) касательная параллельна оси Оу. При 
В начале координат (в особой точке) две ветви кривой, соответствующие знакам плюс и минус перед корнем, взаимно касаются. Такая особая точка называется точкой соприкосновения.
Пример 49. Исследовать кривую у 2 – х 2 (х – 1) = 0.
Решение. Напишем систему уравнений, определяющих особые точки:
Эта система имеет решение х = 0, у = 0. Следовательно, точка (0, 0) есть особая точка кривой. Перепишем данное уравнение в виде 
Исследуем ветвь кривой, соответствующую знаку плюс перед корнем. При увеличении х от 1 до ¥ у увеличивается от 0 до ¥. Производная 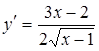
Вторая ветвь кривой, соответствующая знаку минус, симметрична с первой относительно оси Ох.
Точка (0, 0) имеет координаты, удовлетворяющие уравнению, и, следовательно, принадлежит кривой, но вблизи нее нет других точек кривой (рис. 14). Такая особая точка называется изолированной особой точкой.
Задание для самостоятельной работы
Исследовать на особые точки кривые:
148.  . . | 150. 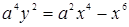 . . |
149. 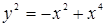 . . | 151.  . . |
152. 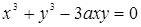 (декартов лист). (декартов лист). | 153. 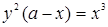 (циссоида). (циссоида). |
154. 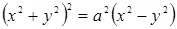 (лемниската). (лемниската). | 155.  (строфоида). (строфоида). |
156. 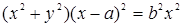
Дата добавления: 2015-07-24 ; просмотров: 2360 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://helpiks.org/4-26553.html

