Метод Ньютона
Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .
- Решение онлайн
- Видеоинструкция
- Оформление Word
Правила ввода функции, заданной в явном виде
- Примеры правильного написания F(x) :
- 10•x•e 2x = 10*x*exp(2*x)
- x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
- x 3 -x 2 +3 = x^3-x^2+3
- Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .
Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:- Отделение корней, то есть установление интервалов [αi,βi] , в которых содержится один корень уравнения.
- f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
- f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
- f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
Геометрическая интерпретация метода Ньютона (метод касательных)
Критерий завершения итерационного процесса имеет вид
Метод интервалов, решение неравенств
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
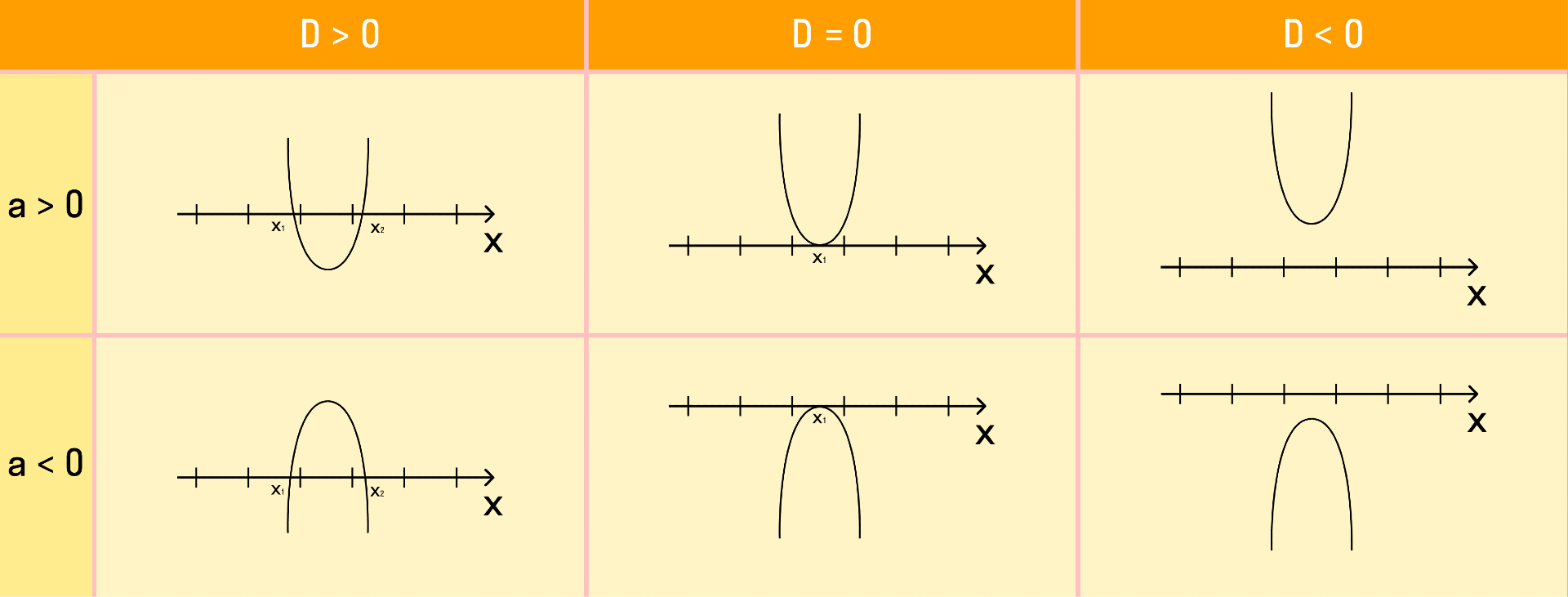
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D 2 + bx + c.
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.
Изобразить координатную прямую и при наличии корней отметить их на ней.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
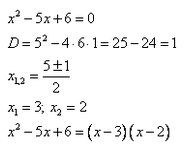
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
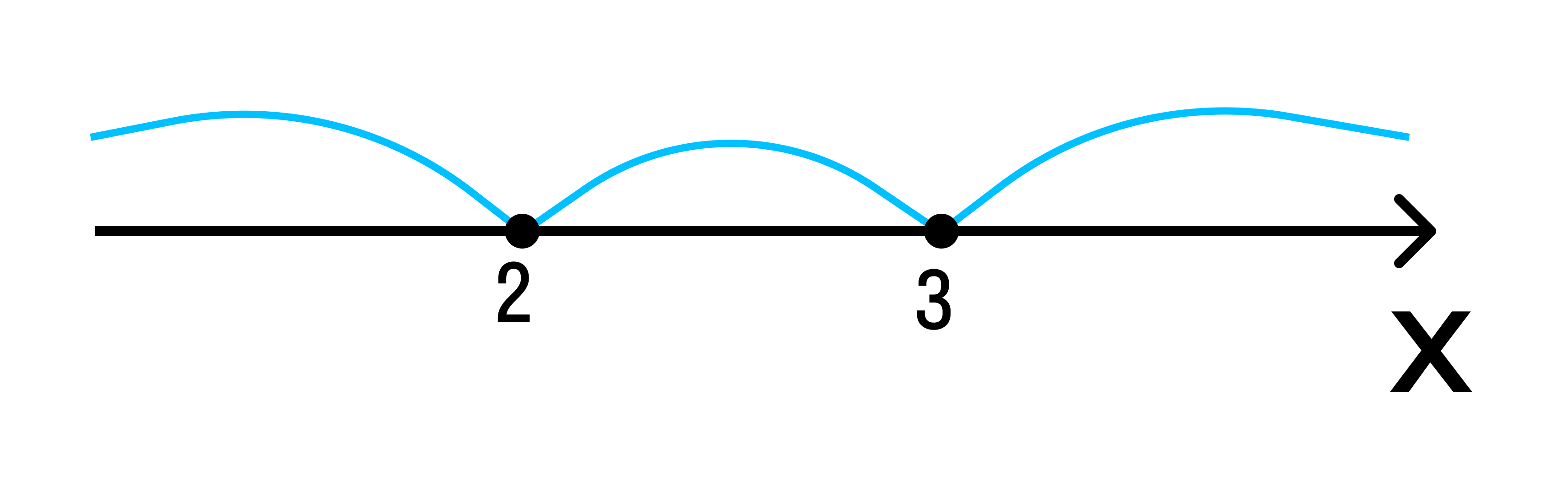
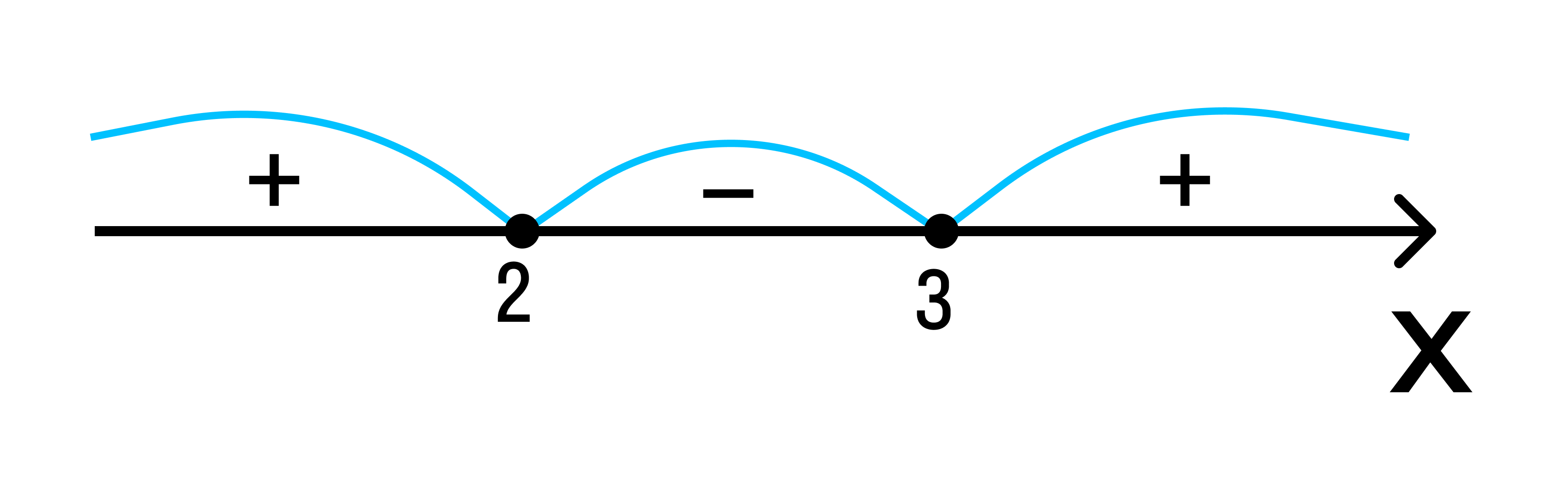
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Применение производной для решения нелинейных уравнений и неравенств
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. \begin
Если две точки экстремума найдены, но \(f(x_1)\cdot f(x_2)=0\), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
| 1) \(x^3+3x^2-4=0\) \(b^2-3ac=9\gt 0 (c=0) \) \(f(x)=x^3+3x^2-4 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-4,\ f(x_2)=0 \) \(f(x_1)\cdot f(x_2)=0\Rightarrow\) два корня  | 2) \(x^3+3x^2-1=0\) \(b^2-3ac=9\gt 0 \) \(f(x)=x^3+3x^2-1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-1,\ f(x_2)=3 \) \(f(x_1)\cdot f(x_2)\lt 0\Rightarrow\) три корня  |
| 3) \(x^3+3x^2+1=0\) \(b^2-3ac=9\gt 0\) \(f(x)=x^3+3x^2+1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=1,\ f(x_2)=5 \) \(f(x_1)\cdot f(x_2)\gt 0\Rightarrow\) один корень  | 4) \(x^3+x^2+x+3=0\) \(b^2-3ac=1-3\lt 0 \) Один корень  |
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения \(\frac 1x+\frac<1>
б) Найдите число корней уравнения \(\frac 1x+\frac<1>
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью \(y=1\). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=\frac1x+\frac<1>
1) ОДЗ: \(x\ne\left\<0;1;3\right\>\)
Все три точки – точки разрыва 2-го рода. \begin
Функция непериодическая.
3) Асимптоты
1. Вертикальные \(x=0, x=1, x=3\) – точки разрыва 2-го рода
2. Горизонтальные: \begin
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: \(k=0\), нет.
4) Первая производная $$ f'(x)=-\frac<1>
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. \(x=0\) – асимптота
Точки пересечения с OX – две, \(0\lt x_1\lt 1,1\lt x_2\lt 3\)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь \(y=k\) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При \(k\lt 0\) — три корня
При \(k=0\) — два корня
При \(k\gt 0\) — три корня
Ответ: а) 3 корня; б) при \(k=0\) два корня, при \(k\ne 0\) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ \sqrt
Исследуем функцию \(f(x)=\sqrt
ОДЗ: \( \begin
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: \(f(1)=0+\sqrt<8>=2\sqrt<2>,\ f(5)=\sqrt<4>+0=2\)
Первая производная: \begin
| \(x\) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| \(f'(x)\) | ∅ | + | 0 | — | ∅ |
| \(f(x)\) | \(2\sqrt<2>\) | \(\nearrow \) | max \(2\sqrt<3>\) | \(\searrow \) | 2 |
Можем строить график:
\(y=a\) — горизонтальная прямая.
Количество точек пересечения \(f(x)\) и \(y\) равно количеству решений.
Получаем:
| $$ a\lt 2 $$ | нет решений |
| $$ 2\leq a\lt 2\sqrt <2>$$ | 1 решение |
| $$ 2\sqrt<2>\leq a\lt 2\sqrt <3>$$ | 2 решения |
| $$ a=2\sqrt <3>$$ | 1 решение |
| $$ a\gt 2\sqrt <3>$$ | нет решений |
По крайней мере одно решение будет в интервале \(2\leq a\leq 2\sqrt<3>\).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство \(\frac<2+\log_3 x>
Разобьем неравенство на совокупность двух систем.
Если \(x\gt 1\), то \(x-1\gt 0\), на него можно умножить слева и справа и не менять знак.
Если \(x\lt 1\), то \(x-1\lt 0\), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: \(x\gt 0\)
Получаем совокупность: \begin
Точка разрыва: \(x=\frac12\) – вертикальная асимптота
Односторонние пределы: \begin
Первая производная: $$ f'(x)=\left(1-\frac<3><2x-1>\right)’=\frac<3><(2x-1)^2>\gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-\frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка \(x=\frac12\)
http://skysmart.ru/articles/mathematic/metod-intervalov-reshenie-neravenstv
http://reshator.com/sprav/algebra/10-11-klass/primenenie-proizvodnoj-dlya-resheniya-nelinejnyh-uravnenij-i-neravenstv/