Найти коэффициенты по каноническому уравнению

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.

Понятие канонического уравнения прямой

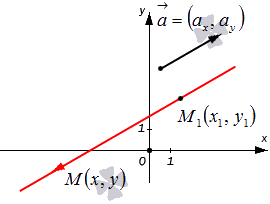
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M 1 ( x 1 , y 1 ) , а также ее направляющего вектора a → = ( a x , a y ) . Попробуем составить уравнение, которое описывало бы эту прямую.

Возьмем плавающую точку M ( x , y ) . Тогда вектор M 1 M → можно считать направляющим для исходной прямой. Его координаты будут равны x — x 1 , y — y 1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).

Множество произвольно взятых точек M ( x , y ) будут определять нужную нам прямую с направляющим вектором a → = ( a x , a y ) только в одном случае – если векторы M 1 M → и a → = ( a x , a y ) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:

Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:

M 1 M → = λ · a → , λ ∈ R

Если преобразовать полученное равенство в координатную форму, то мы получим:

x — x 1 = λ · a x y — y 1 = λ · a y

При условии, что a x ≠ 0 и a y ≠ 0 , получим:

x — x 1 = λ · a x y — y 1 = λ · a y ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x — x 1 a x = y — y 1 a y также называют уравнением прямой в каноническом виде.

Таким образом, с помощью уравнения x — x 1 a x = y — y 1 a y можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a → = ( a x , a y ) и проходит через точку M 1 ( x 1 , y 1 ) .

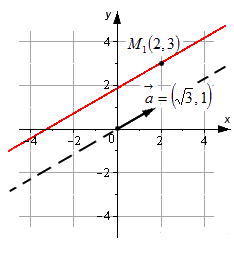
Примером уравнения подобного типа является, например, x — 2 3 = y — 3 1 . Прямая, которая задана с его помощью, проходит через M 1 ( 2 , 3 ) и имеет направляющий вектор a → = 3 , 1 . Ее можно увидеть на рисунке:

Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:

1. Если прямая, имеющая направляющий вектор a → = ( a x , a y ) , проходит через две точки – M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , то уравнение для нее может быть записано как в виде x — x 1 a x = y — y 1 a y , так и x — x 2 a x = y — y 2 a y .

2. Если заданная прямая имеет направляющий вектор с координатами a → = ( a x , a y ) , то множество всех ее векторов можно обозначить как μ · a → = ( μ · a x , μ · a y ) , μ ∈ R , μ ≠ 0 . Таким образом, любое уравнение прямой в каноническом виде x — x 1 μ · a x = y — y 1 μ · a y будет соответствовать этой прямой.

Разберем важный пример задачи на нахождение канонического уравнения.

В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M 1 ( 2 , — 4 ) и имеет направляющий вектор с координатами a → = ( 1 , — 3 ) . Запишите каноническое уравнение, описывающее данную прямую.

Решение

Для начала вспомним общий вид нужного нам канонического уравнения – x — x 1 a x = y — y 1 a y . Подставим в него имеющиеся значения x 1 = 2 , y 1 = — 4 , a x = 1 , a y = — 3 и подсчитаем:

x — x 1 a x = y — y 1 a y ⇔ x — 2 1 = y — ( — 4 ) — 3 ⇔ x — 2 1 = y + 4 — 3

Получившееся в итоге равенство и будет нужным ответом.

Ответ: x — 2 1 = y + 4 — 3

Канонические уравнения прямой на плоскости с a x или a y , равными нулю

Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x — x 1 a x = y — y 1 a y условной и понимать ее как равенство a y ( x — x 1 ) = a x ( y — y 1 ) .

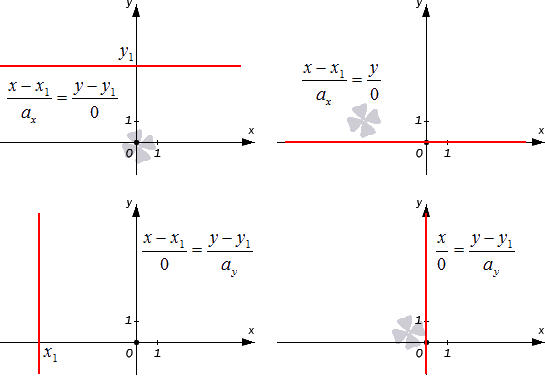
Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x — x 1 0 = y — y 1 a y при a x = 0 , а исходная прямая будет проходить через M 1 ( x 1 , y 1 ) . В таком случае она является параллельной оси ординат (если x 1 = 0 , то она будет с ней совпадать). Докажем это утверждение.

Для этой прямой вектор a → = ( 0 , a y ) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j → = ( 0 , 1 ) .

Если же нулевым является значение второго параметра, то есть a y = 0 , то мы получаем равенство вида x — x 1 a x = y — y 1 0 . Это уравнение описывает прямую, проходящую через M 1 ( x 1 , y 1 ) , которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a → = ( a x , 0 ) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i → = ( 1 , 0 ) .

Проиллюстрируем два частных случая канонического уравнения, описанные выше:

На плоскости задана прямая, параллельная оси O y . Известно, что она проходит через точку M 1 2 3 , — 1 7 . Запишите каноническое уравнение для нее.

Решение

Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j → = ( 0 , 1 ) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:

x — 2 3 0 = y — — 1 7 1 ⇔ x — 2 3 0 = y + 1 7 1

Ответ: x — 2 3 0 = y + 1 7 1

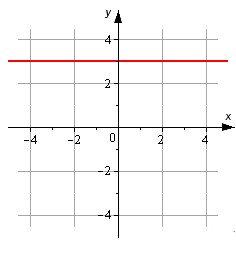
На рисунке изображена прямая. Запишите ее каноническое уравнение.

Решение

Мы видим, что исходная прямая проходит параллельно оси O x через точку M 1 ( 0 , 3 ) . Мы берем координатный вектор i → = ( 1 , 0 ) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.

x — 0 1 = y — 3 0 ⇔ x 1 = y — 3 0

Ответ: x 1 = y — 3 0

Преобразование канонического уравнения прямой в другие виды уравнений

Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.

Стандартной форме записи канонического уравнения x — x 1 a x = y — y 1 a y можно поставить в соответствие систему параметрических уравнений на плоскости x = x 1 + a x · λ y = y 1 + a y · λ . Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ . После этого надо выполнить разрешение получившихся равенств относительно переменных x и y :

x — x 1 a x = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y = λ ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Покажем на примере, как именно выполняется это действие с конкретными числами.

У нас есть прямая, заданная на плоскости с помощью канонического уравнения x + 2 3 = y — 1 11 . Запишите параметрические уравнения исходной прямой.

Решение

Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x + 2 3 = λ y — 1 11 = λ .

Далее можно перейти к формулированию необходимых параметрических уравнений:

x + 2 3 = λ y — 1 11 = λ ⇔ x + 2 = 3 · λ y — 1 = 11 · λ ⇔ x = — 2 + 3 · λ y = 1 + 11 · λ

Ответ: x = — 2 + 3 · λ y = 1 + 11 · λ

Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись a b = c d можно представить в виде a · d = b · c с сохранением смысла. Значит, что x — x 1 a x = y — y 1 a y ⇔ a y ( x — x 1 ) = a x ( y — y 1 ) ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 .

Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров a y = A , — a x = B , — a y x 1 + a x y 1 = C .

Прямая на плоскости описана с помощью канонического уравнения x — 1 2 = y + 4 0 . Вычислите общее уравнение этой прямой.

Решение

Делаем указанные выше действия по порядку.

x — 1 2 = y + 4 0 ⇔ 0 · ( x — 1 ) = 2 · ( y + 4 ) ⇔ y + 4 = 0

Ответ: y + 4 = 0 .

Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.

На плоскости задана прямая с помощью уравнения x + 3 3 = y — 2 2 . Запишите уравнение этой же прямой в отрезках.

Решение

Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.

x + 3 3 = y — 2 2 ⇔ 2 · ( x + 3 ) = 3 · ( y — 2 ) ⇔ 2 x — 3 y + 6 + 2 3 = 0

Далее переходим к формулировке уравнения прямой в отрезках.

2 x — 3 y + 6 + 2 3 = 0 ⇔ 2 x — 3 y = — 6 + 2 3 ⇔ ⇔ 2 — ( 6 + 2 3 ) x — 3 — ( 6 + 2 3 ) y = 1 ⇔ x — 6 + 2 3 2 + y 6 + 2 3 3 = 1 ⇔ x — 3 + 3 + y 3 3 + 2 = 1

Ответ: x — 3 + 3 + y 3 3 + 2 = 1

Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – A x + B y + C = 0 . При условии A ≠ 0 мы можем перенести B y вправо с противоположным знаком. Получим A x + C = — B y . Теперь выносим A за скобки и преобразуем равенство так:

Получившееся уравнение мы записываем в виде пропорции: x + C A — B = y A .

У нас получилось нужное нам каноническое уравнение прямой на плоскости.

А как сделать преобразование, если B ≠ 0 ? Переносим все слагаемые, кроме A x , вправо с противоположными знаками. Получаем, что A x = — B y — C . Выносим — B за скобки:

Формируем пропорцию: x — B = y + C B A

Есть общее уравнение прямой x + 3 y — 1 = 0 . Перепишите его в каноническом виде.

Решение

Оставим с левой стороны только одну переменную x . Получим:

Теперь вынесем — 3 за скобки: x = — 3 y — 1 3 . Преобразуем равенство в пропорцию и получим необходимый ответ:

Ответ: x — 3 = y — 1 3 1

Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.

Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x = x 1 + a x · λ y = y 1 + a y · λ и приравнять обе части равенств. Схема решения выглядит так:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.

Прямая на плоскости описана с помощью системы параметрических уравнений x = 3 + 0 · λ y = — 2 — 4 · λ . Запишите каноническое уравнение для этой прямой.

Решение

Для начала преобразуем исходные уравнения в систему x = 3 + 0 · λ y = — 2 — 4 · λ . Следующим шагом будет выражение параметра в каждом уравнении:

x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

Как решать задачи на составление канонических уравнений

В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.

На плоскости задана прямая, каноническое уравнение которой имеет вид x — 1 2 = y + 1 2 — 3 . Выясните, лежат ли на ней точки M 1 3 , — 3 1 2 и M 2 ( 5 , — 4 ) .

Решение

Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.

3 — 1 2 = — 3 1 2 + 1 2 — 2 ⇔ 1 = 1

Результат говорит нам, что точка M 1 3 , — 3 1 2 принадлежит исходной прямой.

Точно так же поступим и с координатами второй точки:

5 — 1 2 = — 4 + 1 2 — 3 ⇔ 2 = 7 6

Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.

Ответ: первая точка лежит на заданной прямой, а вторая нет.

Есть две точки M 1 ( 2 , 4 ) и M 2 ( — 1 , 3 ) . Будет ли прямая, которая задана в той же плоскости с помощью уравнения x — 2 0 = y — 3 2 , проходить через них?

Решение

Вспомним, что запись x — 2 0 = y — 3 2 можно понимать как 2 · ( x — 2 ) = 0 · ( y — 3 ) ⇔ x — 2 = 0 . Подставим координаты заданных точек в это равенство и проверим.

Начнем с первой точки M 1 ( 2 , 4 ) : 2 — 2 = 0 ⇔ 0 = 0

Равенство верное, значит, эта точка расположена на заданной прямой.

Подставляем данные второй точки: — 1 — 2 = 0 ⇔ — 3 = 0 .

Равенство неверное, значит, точка M 2 ( — 1 , 3 ) не лежит на исходной прямой.

Ответ: через точку M 1 ( 2 , 4 ) прямая проходит, а через M 2 ( — 1 , 3 ) нет.

Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.

Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.

Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.

Прямая на плоскости проходит через точку M 1 ( 0 , — 3 ) и через точку M 2 ( 2 , — 2 ) . Сформулируйте для этой прямой канонической уравнение.

Решение

Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M 1 M 2 → = 2 , 1 . По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:

x — 0 2 = y — ( — 3 ) 1 ⇔ x 2 = y + 3 1

Также можно использовать координаты второй точки. Тогда мы получим: x — 2 2 = y — ( — 2 ) 1 ⇔ x — 2 2 = y + 2 1

Ответ: x 2 = y + 3 1

Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.

Известно, что точка M 1 ( 1 , 3 ) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x 2 = y — 5 . Запишите каноническое уравнение первой прямой.

Решение

Для первой прямой можно определить направляющий вектор a → = 2 , — 5 . Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x — 1 2 = y — 3 — 5

Ответ: x — 1 2 = y — 3 — 5

Через точку M 1 ( — 1 , 6 ) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2 x — 4 y — 7 = 0 . Запишите каноническое уравнение первой прямой.

Решение

Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2 , 4 . Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:

x — ( — 1 ) 2 = y — 6 4 ⇔ x + 1 1 = y — 6 2

Определение коэффициентов канонических уравнений

Коэффициенты при неизвестных 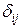и грузовые коэффициенты D_iP системы канонических уравнений – возможные перемещения от единичных сил и нагрузки. У них есть два индекса. Первый индекс i указывает на направление, а второй индекс j (или P) – на причину перемещения.

Методику вычисления этих коэффициентов рассмотрим на примере условной статически неопределимой системы (рис. 7.4 а) и ее основной системы (рис. 7.4 б).

Для определения коэффициентов 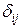рассмотрим два состояния ОС:

1) i-ое единичное состояние – воздействие силы X_i=1 (рис. 7.4 в);

2) j-ое единичное состояние – воздействие силы X_j=1 (рис. 7.4 г).

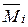
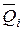
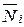
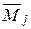
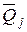
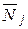
Если в этих состояниях возникают внутренние усилия , , и , , , то возможная работа внутренних сил i-го состояния на деформациях j-го состояния будет:

–V_ij= 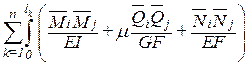dx.

С другой стороны, возможная работа внешних сил i-го состояния на перемещениях j-го состояния равна

По принципу возможных перемещений W_ij=–V_ij. Приравнивая их получаем формулу для вычисления коэффициентов при неизвестных:

d_ij= 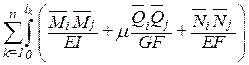dx .

Теорема Максвелла. Перемещение в i-ом направлении от единичной силы в j-ом направлении равна перемещению в j-ом направлении от единичной силы в i-ом направлении, т.е. d_ij=d_ji .

Доказательство. Возможную работу сил i-го единичного состояния (рис. 7.4 в) на перемещениях j-го состояния (рис. 7.4 г) мы уже знаем: W_ij=d_ij. А возможная работа сил j-го состояния на перемещениях i-го состояния равна W_ji=1×d_ji=d_ji. По теореме Бетти W_ij=W_ji. Следовательно, d_ij=d_ji .

Эта теорема позволяет уменьшать объем вычислений при нахождении боковых коэффициентов системы канонических уравнений.

Теперь выведем формулу вычисления грузовых коэффициентов.

Вначале определим возможную работу сил i-го единичного состояния (рис. 7.4 в) на перемещениях грузового состояния (рис. 7.4 д):

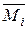
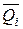
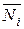
С другой стороны, возможная работа внутренних сил , , i-го единичного состояния на деформациях грузового состояния равна

–V_iP= 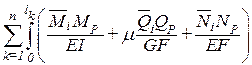dx.

По принципу возможных перемещений W_iP= –V_iP. Приравнивая их получим формулу вычисления грузовых коэффициентов: D_iP= 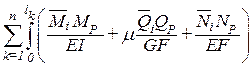dx.

Так как в рамах и балках перемещения определяются в основном изгибными деформациями, то коэффициенты канонических уравнений можно вычислять по сокращенным формулам:

= dx= ,

= dx= ,

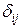
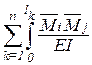
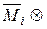
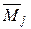
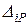
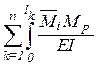
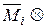
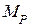
где знак используется для сокращения записи формулы вычисления интеграла Мора и означает условное «произведение» двух эпюр.

В о п р о с ы

1. В чем состоит отличие статически неопределимых систем от статически определимых систем?

2. Как определяется число лишних связей статически неопределимой системы?

3. Каким требованиям должна удовлетворять основная система?

4. В чем заключается физический смысл канонических уравнений метода сил?

5. Чем отличается вычисление коэффициентов при неизвестных от вычисления грузовых коэффициентов?

6. Какое преимущество дает использование теоремы Максвелла?

Уравнение прямой проходящей через две точки

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

• каноническое уравнение,
• параметрическое уравнение,
• общее уравнение прямой,
• уравнение прямой с угловым коэффициентом,
• уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.