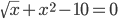Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что 
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Метод бисекции
Метод бисекции или метод деления отрезка пополам — простейший численный метод приближённого нахождения корня уравнения.
Калькулятор, который находит приближенное решение уравнения методом бисекции или методом деления отрезка пополам. Небольшая теория под калькулятором.
Метод бисекции
Метод бисекции
Существует довольно очевидная теорема: «Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но может быть и несколько)». На базе этой теоремы построено несколько методов численного нахождения приближенного значения корня функции. Обобщенно все эти методы называются методами дихотомии, т. е. методами деления отрезка на две части (необязательно равные).
Здесь уже были рассмотрены Метод хорд и Метод секущих, теперь дошла очередь и до самого простого метода дихотомии, называемого методом бисекции, или методом деления отрезка пополам. Как следует из названия, именно в этом методе отрезок делится каждый раз на две равные части. Середина отрезка считается следующим приближением значения корня. Вычисляется значение функции в этой точке, и, если критерий останова не достигнут, выбирается новый интервал. Интервал выбирается таким образом, чтобы на его концах значения функции по прежнему имели разный знак, то есть чтобы он по прежнему содержал корень. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции — и это весьма важное свойство. Недостатком метода является то же самое — метод никогда не сойдется быстрее, т. е. сходимость метода всегда равна сходимости в наихудшем случае.
Итерационная формула проста:
Метод бисекции является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале).
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. Поскольку интервал на каждом шаге уменьшается в два раза, вместо проверки x можно рассчитать количество требуемых итераций.
Найти корень уравнения методом деления отрезка пополам
Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
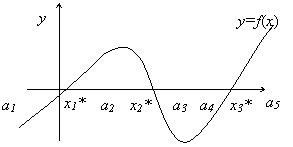
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что 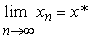
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 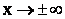
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
Найдем производную f / (x)=3x 2 -12x+3.
Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;
X1=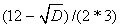
X2=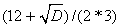
Так как f / (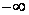
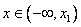
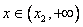
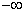
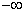
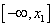
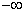
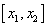
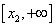
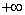
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27 0, f / (x)>0 при 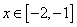
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 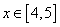
http://planetcalc.ru/3718/
http://pers.narod.ru/study/methods/01.html