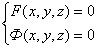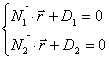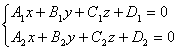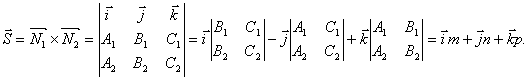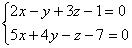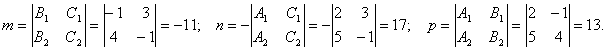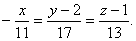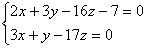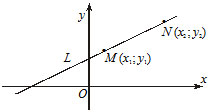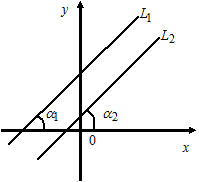Найти направляющие косинусы прямой заданной уравнением

Найти направляющие косинусы прямой заданной уравнением

Уравнение линии в пространстве.

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F ( x , y , z ) = 0 и Ф ( x , y , z ) = 0 – уравнения поверхностей, пересекающихся по линии L .

Тогда пару уравнений

назовем уравнением линии в пространстве.

Уравнение прямой в пространстве по точке и

Возьмем произвольную прямую и вектор ( m , n , p ), параллельный данной прямой. Вектор называется направляющим вектором прямой.

На прямой возьмем две произвольные точки М ₀ ( x ₀ , y ₀ , z ₀ ) и M ( x , y , z ).

z

M ₁

Обозначим радиус- векторы этих точек как и , очевидно, что — = .

Т.к. векторы и коллинеарны , то верно соотношение = t , где t – некоторый параметр.

Итого, можно записать: = + t .

Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

Преобразовав эту систему и приравняв значения параметра t , получаем канонические уравнения прямой в пространстве:

.

Определение. Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:

; .

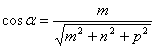
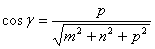
Отсюда получим: m : n : p = cos a : cos b : cos g .

Числа m , n , p называются угловыми коэффициентами прямой. Т.к. — ненулевой вектор, то m , n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.

Уравнение прямой в пространстве, проходящей

через две точки.

Если на прямой в пространстве отметить две произвольные точки M ₁( x ₁, y ₁, z ₁) и M ₂( x ₂, y ₂, z ₂), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

.

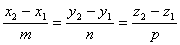
Кроме того, для точки М ₁ можно записать:

.

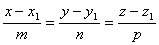
Решая совместно эти уравнения, получим:

.

Это уравнение прямой, проходящей через две точки в пространстве.

Общие уравнения прямой в пространстве.

Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.

Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:

× + D = 0, где

— нормаль плоскости; — радиус- вектор произвольной точки плоскости.

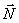
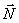
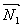
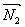
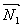
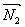
Пусть в пространстве заданы две плоскости: × + D ₁ = 0 и × + D ₂ = 0, векторы нормали имеют координаты: ( A ₁ , B ₁ , C ₁ ), ( A ₂ , B ₂ , C ₂ ); ( x , y , z ).

Тогда общие уравнения прямой в векторной форме:

Общие уравнения прямой в координатной форме:

Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.

Для этого надо найти произвольную точку прямой и числа m , n , p .

При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.

Пример. Найти каноническое уравнение, если прямая задана в виде:

Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

, т.е. А(0, 2, 1).

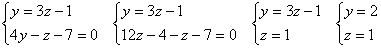
Находим компоненты направляющего вектора прямой.

Тогда канонические уравнения прямой :

Пример. Привести к каноническому виду уравнение прямой, заданное в виде:

Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда :

;

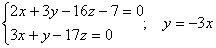
Получаем: A ( -1; 3; 0).

Направляющий вектор прямой: .

Итого:

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Векторная алгебра.
• Проекции вектора. Направляющие косинусы. Неравенство Коши-Буняковского.
• Высшая математика.
• Аналитическая геометрия.

Аналитическая геометрия.

Прямая на плоскости, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой:

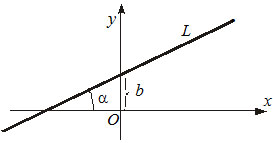
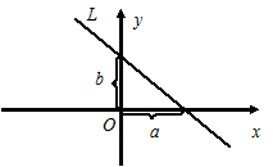
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$

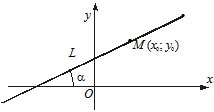
2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $\alpha$ к оси $OX$ $(k=tg\alpha).$

3) $\frac=\frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

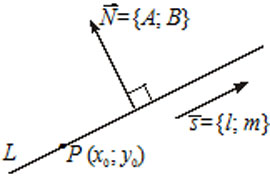
5) $\frac=\frac $ — каноническое уравнение прямой, где $\overline=(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(\overline\parallel L),$ точка $P(x_0, y_0)\in L.$

6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline=(A, B).$ Вектор $\overline N$ называется нормальным вектором прямой.

7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $\overline=(A, B) -$ нормальный вектор прямой $L.$

8) $x\cos\alpha+y\cos\beta-p=0 -$ нормальное уравнение прямой, где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

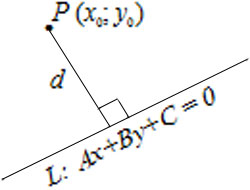
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac<\sqrt>\right|.$$

Расположение двух прямых на плоскости.

Условия параллельности двух прямых:

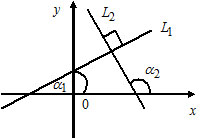
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$

$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$

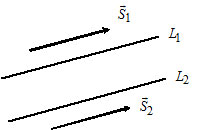
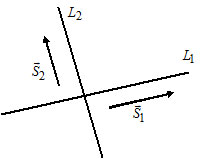
2) Пусть $L_1:$ $\frac=\frac,$ $\overline_1=(l_1, m_1);$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline_1\parallel\overline_2\Leftrightarrow$ $\frac=\frac.$

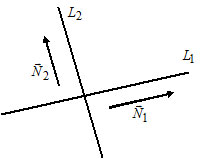
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline_1\parallel\overline_2\Leftrightarrow$ $\frac=\frac.$

Условия перпендикулярности двух прямых:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$

$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$

$L_1\perp L_2\Leftrightarrow$ $k_1\cdot k_2=-1.$

2) Пусть $L_1:$ $\frac=\frac,$ $\overline_1=(l_1, m_1);$

$L_1\perp L_2\Leftrightarrow$ $\overline_1\perp\overline_2\Leftrightarrow$ $\cdot+\cdot=0.$

3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

$L_1\perp L_2\Leftrightarrow$ $\overline_1\perp\overline_2\Leftrightarrow$ $\cdot+\cdot=0.$

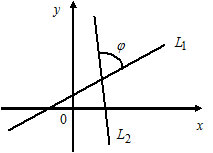
Угол между прямыми:

1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$

$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$

2) Пусть $L_1:$ $\frac=\frac,$ $\overline_1=(l_1, m_1);$

3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

Примеры:

2.141.

а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и нормальным вектором $\overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 6) для уравнения прямых ( $A(x-x_0)+B(y-y_0)=0$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=\overline N(2; 2):$

$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:

Нормальное уравнение прямой имеет вид $x\cos\alpha+y\cos\beta-p=0,$ где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Для нашей прямой имеем $A=1; B=1; C=-1 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac<-1><\sqrt<1+1>>=\frac<1><\sqrt 2>.$

Запишем нормальное уравнение прямой:

Расстояние от начала координат $p=\frac<1><\sqrt 2>.$

Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $\frac<1><\sqrt 2>x+\frac<1><\sqrt 2>y-\frac<1><\sqrt 2>=0;$ $p=\frac<1><\sqrt 2>.$

2.142.

а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и направляющим вектором $\overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 5) для уравнения прямых ( $\frac=\frac$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(l; m)=\overline S(3; -1):$ $\frac<3>=\frac<-1>$

Далее, приведем это уравнение к общему виду:

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Для нашей прямой имеем $A=1; B=3; C=-5 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac<-1><\sqrt<1+9>>=\frac<1><\sqrt<10>>.$

Запишем нормальное уравнение прямой:

Расстояние от начала координат $p=\frac<5><\sqrt <10>>.$

Ответ: $\frac<3>=\frac<-1>;$ общее уравнение $x+3y-5=0;$ нормальное уравнение прямой $\frac<1><\sqrt <10>>x+\frac<3><\sqrt <10>>y-\frac<5><\sqrt <10>>=0;$ $p=\frac<5><\sqrt <10>>.$

2.143.

а) Прямая $L$ задана двумя своими точками $M_1(1; 2)\in L$ и $M_2(-1; 0)\in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

Решение.

Подставим в формулу 3) для уравнения прямых ($\frac=\frac$ ) соответственно координаты точек $M_1(1; 2)= (x_1; y_1) $ и $M_2(-1; 0)=(x_2; y_2):$ $\frac<-1-1>=\frac<0-2>\Rightarrow \frac<-2>=\frac<-2>.$

Далее, приведем это уравнение к общему виду:

Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Для нашей прямой имеем $A=1; B=-1; C=1 \Rightarrow sgn C=1.$ Таким образом, $\mu=-\frac<1><\sqrt<1+1>>=-\frac<1><\sqrt<2>>.$

Запишем нормальное уравнение прямой:

Расстояние от начала координат $p=\frac<1><\sqrt <2>>.$

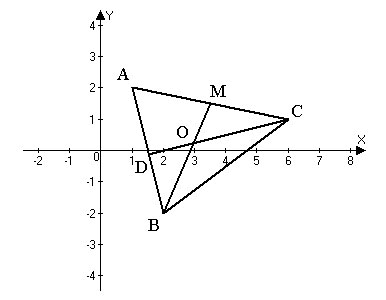
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:

1) Найти уравнение стороны $AB;$

2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$

3) найти угол между высотой $CD$ и медианой $BM.$

Решение.

1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $\frac=\frac. $

В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$

Подставляем координаты точек в уравнение прямой. Получаем $$\frac<2-1>=\frac<-2-2>\Rightarrow x-1=\frac<-4>.$$ Запишем общее уравнение прямой $AB$:

$-4(x-1)=y-2\Rightarrow$ $-4x+4=y-2\Rightarrow$ $4x+y-6=0.$

2) Уравнение прямой $CD$ найдем, пользуясь уравнением ( 6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline=(A, B).$

В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$

Таким образом, $$(x_0; y_0)=C=(6; 1);\quad\overline=\overline=(2-1; -2-2)=(1; -4).$$

Подставляем эти координаты в уравнение прямой:

$1(x-6)-4(y-1)=0\Rightarrow x-6-4y+4=0 \Rightarrow x-4y-2=0.$

То есть, уравнение прямой $CD:$ $x-4y-2=0.$

Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$

Решим систему методом исключений:

Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$

3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.

Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=\frac<2>; y_M=\frac<2>.$

Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой

$3.5(x-2)=1.5(y+2)\Rightarrow 3.5x-7=1.5y+3 \Rightarrow 3.5x-1.5y-10=0.$

Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле

где $L_1: A_1x+B_1y+C_1=0,$ $\overline_1=(A_1, B_1);$

$L_2: A_2x+B_2y+C_2=0,$ $\overline_2=(A_2, B_2).$

Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$

Ответ: 1) $AB: 4x+y-6=0.$

2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$

Решение.

Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$

Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$

Далее, чтобы найти координаты точки $B,$ решим систему уравнений:

$$\Rightarrow\left\<\beginx=y\\y=\frac<25><6>.\end\right.$$ Мы нашли координаты точки $B\left(\frac<25><6>, \frac<25><6>\right).$

Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $\left(\frac=\frac \right):$

$$\Rightarrow\frac<1>=\frac<7>\Rightarrow 7x-28=y-3\Rightarrow 7x-y-25=0.$$

Ответ: $7x-y-25=0.$

2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.

Решение:

Найдем уравнение диагонали $AC:$

Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $\overline=(1; -1).$ Прямая, перпендикулярная прямой $AC$ является параллельной нормальному вектору $\overline$. Таким образом, уравнение прямой $BD$ запишем по формуле 5) $\left(\frac=\frac\right),$ где $(x_0, y_0)=O(0; 2),$ $(l, m)=\overline=(1, -1):$

$$\frac<1>=\frac<-1>\Rightarrow x=-y+2 \Rightarrow x+y-2=0.$$

Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=\sqrt<(0-1)^2+(2-3)^2>=\sqrt<2>.$

Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$

Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой ( 3) — $\frac=\frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$

Деление отрезка в заданном отношении (векторный и координатный способы).

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline,$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $\overline=r_1,$ $\overline=r_2,$ $\overline=r.$ Так как, $$\overline=r-r_1, \overline=r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac<1+\lambda>.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac<1+\lambda>, y=\frac<1+\lambda>, z=\frac<1+\lambda>.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac=\frac<1><2>;$$ $$x_C=\frac<1+\lambda_1>=\frac<3+\frac<1><2>\cdot 6><1+\frac<1><2>>=4;$$

Далее находим координаты точки $D:$

Ответ: $(4, 0)$ и $(5, 2).$

2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

Аналогичные равенства запишем для точки $D:$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$

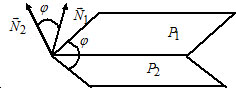
Взаимное расположение плоскостей, угол между плоскостями.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

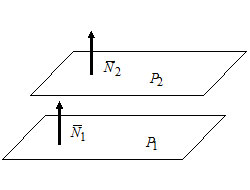
Условие параллельности двух плоскостей:

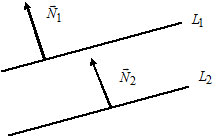
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $\overline_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $\overline_2=(A_2, B_2, C_2).$

Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $\overline_1\parallel\overline_2\Leftrightarrow$ $\frac=\frac=\frac.$

Условия перпендикулярности двух плоскостей:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $\overline_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $\overline_2=(A_2, B_2, C_2).$

$P_1\perp P_2\Leftrightarrow$ $\overline_1\perp\overline_2\Leftrightarrow$ $\cdot+\cdot+C_1\cdot C_2=0.$

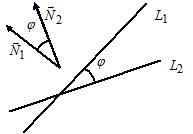
Угол между плоскостями:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $\overline_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $\overline_2=(A_2, B_2, C_2).$

Примеры.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1\parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.

2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: -x+2y-z+1=0, \Rightarrow\overline_1=(-1, 2, -1);$

$P_2: y+3z-1=0, \Rightarrow\overline_2=(0, 1, 3).$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

Ответ: Плоскости пересекаются. $\cos\widehat<(P_1, P_2)>=\frac<1><2\sqrt<15>>.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: x-y+1=0, \Rightarrow\overline_1=(1, -1, 0);$

$P_2: y-z+1=0, \Rightarrow\overline_2=(0, 1, -1).$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

Ответ: Плоскости пересекаются. $\cos\widehat<(P_1, P_2)>=\frac<1><2>.$

2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$

Решение.

Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$

$P_1: 2x-y+5z+3=0, \Rightarrow\overline_1=(2, -1, 5);$

$P_2: x+3y-z-7=0, \Rightarrow\overline_2=(1, 3, -1).$

Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$

Ответ: $-2x+y+z+2=0.$

Домашнее задание.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1\parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.

Направляющий вектор прямой, координаты направляющего вектора прямой

С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.

В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.

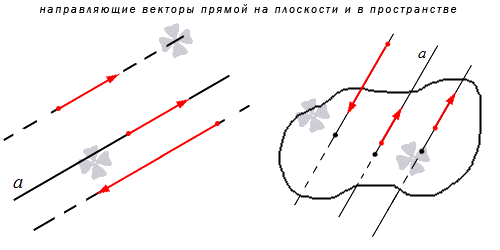
Что такое направляющий вектор прямой

Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.

Сформулируем, что такое направляющий вектор.

Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.

Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .

Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.

Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .

Как вычислить координаты направляющего вектора по уравнениям прямой

Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.

1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.

Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .

Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.

Приведем пример задачи.

В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.

Решение

Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.

Ответ: 4 , — 3 .

Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.

У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.

Решение

Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.

Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0

Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .

А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.

У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.

Решение

В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.

Ответ: ( 0 , 1 )

А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.

1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.

2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.

3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .

Самым простым является первый подход. Проиллюстрируем его на примере задачи.

Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.

Решение

Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:

3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10

Получившееся равенство преобразовываем и получаем:

3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3

Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3

К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.

Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.

Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:

1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z

2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z

Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.

Рассмотрим конкретную задачу.

Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.

Решение

В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.

Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0

Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .

Решение

Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .

Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.

Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?

Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.

Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.

Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.

Решим задачу, в которой применяется этот подход.

Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .

Решение

Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .

У нас получится:

n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →

Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.

Ответ: — 20 , 10 , 0

В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.