Найти общее решение уравнения uxy 0

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Лекция 1. Введение

Будем рассматривать функции вида U=U(x₁,x₂,…,x_n), x=(x₁,x₂. x_n) .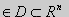

В частных случаях:

В этом случае переменные x, y, z называются пространственными переменными, t — время.

Условимся для простоты записи обознать частные производные , и т.д.

Определение. Дифференциальным уравнением с частными производными называется уравнение вида

Другими словами — это уравнение, связывающее независимые переменные x_i, неизвестную функцию U и ее частные производные до порядка k.

Определение. Порядком дифференциального уравнения с частными производными называется высший из порядков частных производных, входящих в это уравнение.

Определение. Решением уравнения с частными производными порядка k называется функция U=U(x₁, x₂ , … ,x_n), определенная в некоторой области , которая имеет производные до порядка k и при подстановке в уравнение обращает его в тождество по (x₁, x₂, … , x_n).

Определение. Дифференциальное уравнение с частными производными называется линейным, если функция U и ее частные производные входят в него линейным образом.

Запишем общий вид линейного уравнения с двумя переменными:

в случае уравнения 1-го порядка:

в случае уравнения 2-го порядка:

Функции a(x, y), b(x, y), … , A(x, y ), B(x, y) … — коэффициенты (заданные функции), f(x, y)— правая часть (заданная функция) линейного дифференциального уравнения.

Определение. Дифференциальное уравнение с частными производными называется однородным, если его правая часть тождественно равна нулю, т.е при всех (x,y) D.

Определение. Дифференциальное уравнение с частными производными называется неоднородными, если его правая часть тождественно не равна нулю, т.е. при некоторых (x,y) D.

Определение. Если коэффициенты линейного дифференциального уравнения — постоянные, то такое уравнение называется линейным дифференциальным уравнением с постоянными коэффициентами.

Левая часть уравнения (1) или (2) обычно обозначается через LU и называется линейным дифференциальным оператором с частными производными порядка 1 или 2, соответственно. Тогда линейное неоднородное дифференциальное уравнение будет иметь вид LU = f(x ,y), а линейное однородное дифференциальное уравнение будет иметь вид LU = 0.

Определение. Выражение вида или называется оператором Лапласа, соответственно, на плоскости или в пространстве.

Условимся для более краткой записи сокращать (линейное) дифференциальное уравнение до (Л)ДУ, линейное (не)однородное дифференциальное уравнение до ЛОДУ (ЛНДУ).

Среди ЛДУ второго порядка есть уравнения, которые имеют особое значение. Перечислим их :

1. Уравнение Лапласа— уравнение вида ∆ U =0 ( n =2,3)- ЛОДУ 2-го порядка.

Уравнение Пуассона— уравнение вида ∆ U = f ( n =2,3)- ЛНДУ 2-го порядка.

2. Волновое уравнение— уравнение вида U_tt=a 2 ΔU, где ΔU = U_xx+U_yy на плоскости или ΔU = U_xx+U_yy+U_zz в пространстве. Одномерное волновое уравнение (на прямой) — уравнение вида U_tt=a 2 U_xx .

3. Уравнение теплопроводности- уравнение вида U_t = a 2 ∆ U , где где ΔU = U_xx+U_yy на плоскости или ΔU = U_xx+U_yy+U_zz в пространстве . Одномерное уравнение теплопроводности (на прямой)- уравнение вида U_t = a 2 U_xx .

Именно эти уравнения являются основными уравнениями математической физики.

Основные свойства решений ЛДУ (в том числе обыкновенных).

2. Если U ₁ и U ₂ — решения ЛНДУ LU = f , то ( U ₁— U ₂) — решение ЛОДУ LU =0 , соответствующего данному ЛНДУ.

3. Принцип суперпозиции решений: если U ₁ и U ₂ — решенияЛНДУ LU ₁= f ₁ и LU ₂= f ₂ соответственно , то ( U ₁+ U ₂)- решение ЛНДУ L ( U ₁+ U ₂)= f ₁+ f ₂.

Кроме этих свойств решения ДУ с частными производными могут обладать некоторыми «особыми» свойствами.
4. ДУ с частными производными могут иметь бесконечное множество линейно независимых решений. Из этих решений можно составить ряд с произвольными коэффициентами. Тогда, если ряд сходится и его можно почленно дифференцировать необходимое число раз, то он также является решением ДУ.

Рассмотрим функции двух переменных U_n = sinnxcosny . Из теории тригонометрических рядов следует, что система функций n> ортогональна в области [-π,π] x [-π,π] и, следовательно, линейно независимая. Нетрудно проверить, что они являются частными решениями ДУ U_xx = U_yy . Пусть ряд сходится и его можно дважды почленно дифференцировать. Тогда функция также является решением ДУ U_xx = U_yy.

5. Решениями ДУ с частными производными могут быть любые функции (при условии, что они имеют соответствующие частные производные).

Возьмем уравнение U_xy = 0 и решим его. Для этого первый раз будем интегрировать по x (считая y постоянной величиной):

Полученное равенство проинтегрируем еще раз, теперь уже по y, считая x постоянной величиной:

где C₁(y) — первообразная от произвольной функции φ( y ) и потому также произвольная (дифференцируемая) функция. Таким образом, общее решение уравнения U_xy=0 зависит от двух произвольных функций.

Классификация дифференциальных уравнений с частными производными.

Уравнения с частными производными можно классифицировать по разным признакам.

1. П о порядку уравнений: U_t=U_xx ( уравнение 2-го порядка), U_t=U_x (уравнение 1-го порядка), U_t=U_xxx + sinx ( уравнение третьего порядка).

2. По числу независимых переменных: U _t=U_xx (уравнение с 2-мя переменными), — уравнение с тремя переменными.

3. ДУ с частными производными могут быть линейными и нелинейными. Линейные уравнения в свою очередь бывают однородными и неоднородными.

4. ЛДУ 2-го порядка классифицируются по тип у :

а) Гиперболический тип ( в области D ), если выражение δ( x , y )= B 2 — AC >0 для любых (x, y) D, где A, B, C — коэффициенты в уравнении (2)

б) Эллиптический тип (в области D ), если выражение δ( x , y )= B 2 — AC x , y) D

в) Параболический тип (в области D ), если выражение δ( x , y )= B 2 -AC = 0 для любых ( x , y) D.

Отметим, что тип уравнения определяется только коэффициентами A , B , C при производных 2-го порядка. При невырожденной замене переменных тип не меняется.

г) Смешанный тип, если в области D уравнение имеет разный тип в разных точках.

Пример. Рассмотрим уравнение

yU_xx + U_yy = 0
Оно возникает в газовой динамике и называется уравнением Трикоми. Для этого уравнения выражение δ(x,y) = B 2 — AC = -y. Тогда при y>0 выражение δ(x,y) 0, следовательно, уравнение гиперболического типа, а при y=0, соответсвенно, δ(x,y)=0 и уравнение имеет параболический тип (см. рис. 1)

Замечания.
1. Уравнения с постоянными коэффициентами имеют один тип на всей области определения. Так, например, волновое уравнение на плоскости и в пространстве имеет гиперболический тип, уравнение теплопроводности на плоскости и в пространстве — параболический тип, а уравнение Лапласа — эллиптический тип.

2. Классификация ЛДУ с большим числом переменных почти аналогична.

Канонический вид ЛДУ 2-го порядка с частными производными (n=2).

В случае двух переменных существует невырожденная замена переменных ξ = ξ ( x , y ), η = η ( x , y ) ( где ξ ( x , y ), η ( x , y ) дважды непрерывно дифференцируемые функции и якобиан такая, что уравнение (2) приводится к одному из следующих видов:

1. U _ξξ -U _ηη =f( ξ , η ,U,U _ξ ,U _η ) ( гиперболический тип ).

2. U _ξξ +U _ηη =f( ξ , η ,U,U _ξ ,U _η ) ( эллиптический тип ).

3. U ηη = f ( ξ , η , U , U_ξ , U_η ) (параболический тип).

Определение. Уравнения вида 1-3 называются каноническими уравнениями.

В соответствии с этим определением одномерное волновое уравнение и уравнение теплопроводности при a =1 имеют канонический вид.

Для уравнений с постоянными коэффициентами всегда существует линейная замена переменных ξ=ax+by, η=cx+dy, с помощью которой уравнение можно привести к каноническому виду.

Замечание. В случае n >2 переменных уравнение второго порядка всегда можно привести к каноническому виду в любой точке, однако в области это не всегда можно сделать.

Зачем нужно классифицировать и приводить уравнения к каноническому виду?

Типом уравнения определяются основные свойства решений.
Три типа уравнений соответствуют трем видам физических процессов- волновым, диффузионным и стационарным.

Волновые процессы: колебания сред, сооружений, электрические, звуковые, электромагнитные колебания.

Диффузионные процессы: тепломассоперенос (температура,диффузия газов).

Стационарные процессы:стационарное распределение температуры, установившиеся колебания сред, задачи дифракции, потенциальное течение жидкости, электростатический потенциал.

Канонические уравнения хорошо изучены. У равнение общего вида сводится к каноническому, которое хорошо изучено. Часто можно найти его решение аналит и чески и вернуться к прежним переменным.
Д ля канонических уравнений разработанны ч исленные методы решения .

Найти общее решение уравнения uxy 0

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Лекция 1. Введение

Основные свойства решений ЛДУ (в том числе обыкновенных).

Классификация дифференциальных уравнений с частными производными.

Канонический вид ЛДУ 2-го порядка с частными производными (n=2).

Решением уравнения Uxx + Uy = 0 является функция U = eycosx U = e-ysinx U = e-xsiny

Ваш ответ

решение вопроса

Похожие вопросы