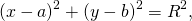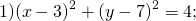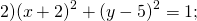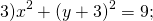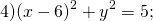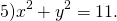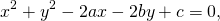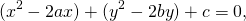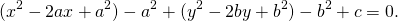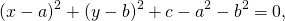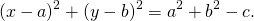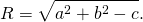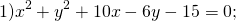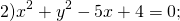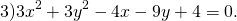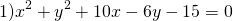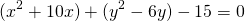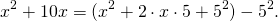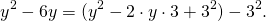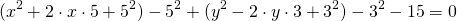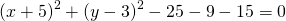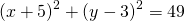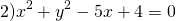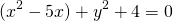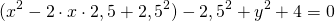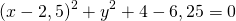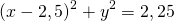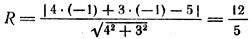Найти ординату центра окружности заданной уравнением

Уравнение окружности по заданному центру и радиусу в различных формах

Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором

Уравнение окружности по заданному центру и радиусу в различных формах

Центр окружности

Уравнение окружности

Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:

• общее уравнение окружности
• стандартное уравнение окружности 1
• параметрическое уравнение окружности
• уравнение окружности в полярных координатах

Общее уравнение окружности

Общее уравнение окружности с центром и радиусом выглядит так:
,
где

В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.

Стандартное уравнение окружности

Стандартное уравнение окружности с центром и радиусом выглядит так:

Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.

Параметрическое уравнение окружности

Параметрическое уравнение окружности с центром и радиусом выглядит так:

Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.

Уравнение окружности в полярных координатах

Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.

Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩

Найти ординату центра окружности заданной уравнением

Как искать ординату центра окружности

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Как искать ординату центра окружности

Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно

Это задание ещё не решено, приводим решение прототипа.

Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).

Диагональ прямоугольника образует два прямоугольных треугольника. Диагональ равна диаметру окружности, описанной около треугольника, следовательно, центр окружности лежит на середине диагонали прямоугольника. Тогда можно легко найти координаты центра окружности.

Материалы к занятию по теме «Параметр в уравнении окружности»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Материалы для занятия по теме

«Параметр в уравнении окружности»

1. Уравнение окружности.

(х ‒ х ₀ )² + (у ‒ у ₀ )² = R ², где А(х ₀ ; у ₀ ) ‒ центр окружности, R ‒ радиус.

х² + у² = R ² ‒ уравнение окружности с центром в начале координат.

2. Параметр – радиус.

Если а = 0, то (х ‒ х ₀ )² + (у‒ у ₀ )² = 0, то есть А(х ₀ ; у ₀ ) – точка.

Если а ˂ 0, то ни окружность, ни точка не существуют.

Если а > 0, то R =, на плоскости – концентрические окружности с центром (х ₀ ; у ₀ ).

Пример. (х ‒ 2)² + (у + 2)² = а (а > 0)

3. Параметр в одной из координат центра.

Одна координата с параметром: (х ‒ 2а)² + (у + 3)² = 9. У центра окружности меняется абсцисса, ордината постоянна. Значит, центры окружностей зафиксированы на прямой у = ‒3.

Задание : подставляя разные значения параметра а, определите координаты центров нескольких окружностей и выполните построение.

Аналогично: (х‒3)² +(у ‒ 2а)² = 9. У центра окружности меняется ордината, абсцисса постоянна. Центры окружностей зафиксированы на прямой х=3.

Задание: построить несколько окружностей, удовлетворяющих последнему уравнению.

4. Параметр в обеих координатах центра.

(х ‒ а)² + (у ‒ а)² = 1. Обе координаты с параметром.

Центр окружности ‒ точка А (а ; а). Так как абсцисса и ордината равны, то все точки такие находятся на прямой у = х. Тогда данное уравнение задает множество окружностей , центры которых лежат на прямой у = х , а радиус равен 1.

Задание : построить несколько окружностей, удовлетворяющих следующему уравнению (х ‒ а)² + (у + 2а)² = 4.

Подсказка. Найдем координаты центра окружности: (х ‒ а)² + (у ‒ (‒2а))² = 4

А(а;-2а), значит центры окружностей лежат на прямой у = ‒2х, радиус равен 2.

5. Параметр в координатах центра и в радиусе.

( х ‒ а)² + (у‒ 2а ‒1 )² = а². Это окружности с центрами на прямой у = 2а + 1, радиус равен а. При а=0 – точка.

Задания для самостоятельной работы.

№ 1. Указать центр, радиус и построить каждую окружность , заданную уравнением:

а) (х ‒ 3)² + (у + 2)² = 16; б) (х + 1)² + (у ‒ 4)² = 10.

№ 2. Выяснить, какие из данных уравнений являются уравнениями окружности. Найти координаты центра и радиус каждой окружности:

а) х² + у² + 8х ‒ 4у + 40 = 0;

б) х² + у² ‒ 2х + 4у ‒ 20 = 0;

в) х² + у² ‒ 4х ‒ 2у + 1 = 0.

№ 3. Выделить уравнение окружности, указать ее центр и радиус в задачах с параметром. Описать расположение графика уравнения на координатной плоскости. Выполнить построение:

а) х² + у² + 2ах ‒ 4у + а² ‒ 1 = 0;

б) х² + у² ‒ 6х + 4ау + 4а² = 0;

в) х² + у² ‒ 2а( х ‒ у ) = 4 ‒ 2а².

1.Геометрия. 7-9 классы : учебник для общеобразовательных организаций с приложением на электронном носителе / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]. – 3-е изд.-М. : Просвещение, 2014.-383 с.

2.Шестаков С.А. ЕГЭ 2014. Математика. Задача С5. Задачи с параметром / Под ред. А.Л.Семенова и И.В.Ященко. – М.:МЦМНО. 2014.-240 с.

Дистанционные курсы для педагогов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 927 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 321 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 700 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

• Сергеева Татьяна ВладиславовнаНаписать 525 15.02.2020

Номер материала: ДБ-1001835

15.02.2020 34

15.02.2020 7

15.02.2020 39

15.02.2020 35

15.02.2020 83

15.02.2020 33

15.02.2020 11

15.02.2020 125

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

530 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет

Время чтения: 3 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Китае приняли закон о сокращении нагрузки на школьников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

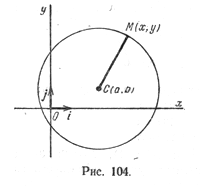
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = \( \sqrt <(x — a)^2 + (у — b)^2>\), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

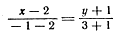
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

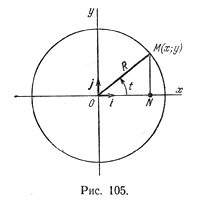
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем