Найти параметрические уравнения плоскости по уравнениям

Уравнения прямых и плоскостей

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,\label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть \(A^<2>+B^<2>+C^ <2>\neq 0\). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,\label
$$
при условии \(A^<2>+B^ <2>\neq 0\).

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения \eqref и \eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol-\boldsymbol_ <0>= t\boldsymbol.\label
$$

Наоборот, какое бы число мы ни подставили в формулу \eqref в качестве \(t\), вектор \(\boldsymbol\) в этой формуле определит некоторую точку на прямой.

Уравнение \eqref называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol

\) и \(\boldsymbol\) ее направляющие векторы, а через \(\boldsymbol_<0>\) — радиус-вектор ее начальной точки \(M_<0>\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol\) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol

\) и \(\boldsymbol\) не коллинеарны, в этом и только этом случае \(\boldsymbol-\boldsymbol_<0>\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_<1>\) и \(t_<2>\), что
$$
\boldsymbol-\boldsymbol_ <0>= t_<1>\boldsymbol

+t_<2>\boldsymbol.\label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_<1>\) и \(t_<2>\). Наоборот, какие бы числа мы ни подставили как значения \(t_<1>\) и \(t_<2>\), уравнение \eqref определит некоторую точку плоскости.

Пусть \((x, y, z)\) и \((x_<0>, y_<0>, z_<0>)\) — координаты точек \(M\) и \(M_<0>\) соответственно, а векторы \(\boldsymbol

\) и \(\boldsymbol\) имеют компоненты \((p_<1>, p_<2>, p_<3>)\) и \((q_<1>, q_<2>, q_<3>)\). Тогда, раскладывая по базису обе части уравнения \eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>,\ y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>,\ z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.\label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой \(M_<0>(x_<0>, y_<0>)\) и направляющим вектором \(\boldsymbol(a_<1>, a_<2>)\) может быть записано в виде \eqref.

Уравнение \eqref линейное. Действительно, после преобразования оно принимает вид \(a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0\), то есть \(Ax+By+C = 0\), где \(A = a_<2>\), \(B = -a_<1>\) и \(C = a_<1>y_<0>-a_<2>x_<0>\).

Вектор с координатами \((-B, A)\) можно принять за направляющий вектор прямой с уравнением \eqref в общей декартовой системе координат, а точку \eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор \(\boldsymbol(A, B)\) перпендикулярен прямой с уравнением \eqref.

Действительно, в этом случае \((\boldsymbol, \boldsymbol) = -BA+AB = 0\).

Пусть в уравнении прямой \(Ax+By+C = 0\) коэффициент \(B\) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,\label
$$
где \(k = -A/B\), а \(b = -C/B\). Мы видим, что к равно отношению компонент направляющего вектора: \(k = a_<2>/a_<1>\) (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора \(a_<2>/a_<1>\) называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от \(\boldsymbol_<1>\) к \(\boldsymbol_<2>\) (рис. 6.4).

Рис. 6.4. \(k=\operatorname\varphi = -1\). Прямая \(y=-x+1/2\)

Положив \(x = 0\) в уравнении \eqref, получаем \(y = b\). Это означает, что свободный член уравнения \(b\) является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой \(B = 0\) и ее уравнение нельзя представить в виде \eqref, то обязательно \(A \neq 0\). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид \(x = x_<0>\), где \(x_ <0>= -C/A\) — абсцисса точки пересечения прямой с осью абсцисс.

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка \(M\) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки \(M_<0>\) компланарна направляющим векторам \(\boldsymbol

\) и \(\boldsymbol\). Эту компланарность можно выразить и равенством
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol

, \boldsymbol) = 0.\label
$$
Вектор \(\boldsymbol = [\boldsymbol

, \boldsymbol]\) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение \eqref в виде
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0.\label
$$

Уравнения \eqref и \eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в \eqref \(D = -(\boldsymbol_<0>, \boldsymbol)\), получим
$$
(\boldsymbol, \boldsymbol)+D = 0.\label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные \eqref и \eqref,
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0\ \mbox<или>\ (\boldsymbol, \boldsymbol)+C = 0.\nonumber
$$
Первое из них выражает тот факт, что вектор \(\boldsymbol-\boldsymbol_<0>\) перпендикулярен ненулевому вектору \(\boldsymbol\), перпендикулярному направляющему вектору \(\boldsymbol\), и потому коллинеарен \(\boldsymbol\).

Пусть \(x, y, z\) — компоненты вектора \(\boldsymbol\) в общей декартовой системе координат. Тогда скалярное произведение \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\) при \(\boldsymbol \neq 0\) записывается линейным многочленом \(Ax+By+Cz+D\), где \((A^<2>+B^<2>+C^ <2>\neq 0)\).

Обратно, для любого линейного многочлена найдутся такие векторы \(\boldsymbol_<0>\) и \(\boldsymbol \neq 0\), что в заданной общей декартовой системе координат \(Ax+By+Cz+D = (\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Первая часть предложения очевидна: подставим разложение вектора \(\boldsymbol\) по базису в данное скалярное произведение:
$$
(x\boldsymbol_<1>+y\boldsymbol_<2>+z\boldsymbol_<3>-\boldsymbol_<0>, \boldsymbol),\nonumber
$$
раскроем скобки и получим многочлен \(Ax+By+Cz+D\), в котором \(D = -(\boldsymbol_<0>, \boldsymbol)\) и
$$
A = (\boldsymbol_<1>, \boldsymbol),\ B = (\boldsymbol_<2>, \boldsymbol),\ C = (\boldsymbol_<3>, \boldsymbol)\label
$$
\(A\), \(B\) и \(C\) одновременно не равны нулю, так как ненулевой вектор \(\boldsymbol\) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор \(\boldsymbol\) из равенств \eqref, считая \(A\), \(B\) и \(C\) заданными. Из ранее доказанного утверждения 10 следует, что
$$
\boldsymbol = \frac_<2>, \boldsymbol_<3>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<3>, \boldsymbol_<1>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<1>, \boldsymbol_<2>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>.\label
$$

Вектор \(\boldsymbol_<0>\) должен удовлетворять условию \(D = -(\boldsymbol_<0>, \boldsymbol)\). Один из таких векторов можно найти в виде \(\boldsymbol_ <0>= \lambda \boldsymbol\). Подставляя, видим, что \(-\lambda(\boldsymbol, \boldsymbol) = D\), откуда \(\boldsymbol_ <0>= -D\boldsymbol/|\boldsymbol|^<2>\).

Итак, мы нашли векторы \(\boldsymbol\) и \(\boldsymbol_<0>\) такие, что линейный многочлен записывается в виде
$$
x(\boldsymbol_<1>, \boldsymbol)+y(\boldsymbol_<2>, \boldsymbol)+z(\boldsymbol_<3>, \boldsymbol)-(\boldsymbol_<0>, \boldsymbol),\nonumber
$$
который совпадает с требуемым \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Если система координат декартова прямоугольная, то вектор с компонентами \(A\), \(B\), \(C\) является нормальным вектором для плоскости с уравнением \(Ax+By+Cz+D = 0\).

Это сразу вытекает из формул \eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению \eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, \(\alpha_<1>, \alpha_<2>\), должны быть пропорциональны компонентам — \(B\), \(A\) направляющего вектора прямой.

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B.\label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения \eqref выполнено (с тем же \(\lambda\)) равенство
$$
C_ <1>= \lambda C.\label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами \((-B, A)\) и \((-B_<1>, A_<1>)\) — направляющие векторы прямых.

Докажем вторую часть. В равенствах \eqref и \eqref \(\lambda \neq 0\), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид \(Ax+By+C = 0\) и \(\lambda(Ax+By)+C_ <1>= 0\) при некотором \(\lambda\). Если, кроме того, существует общая точка \(M_<0>(x_<0>, y_<0>)\) обеих прямых, то \(Ax_<0>+By_<0>+C = 0\) и \(\lambda(Ax_<0>+By_<0>)+C_ <1>= 0\). Вычитая одно равенство из другого, получаем \(C_ <1>= \lambda C\), как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0,\ A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B,\ C_ <1>= \lambda C.\label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений \eqref выполнено (с тем же \(\lambda\)) равенство
$$
D_ <1>= \lambda D.\label
$$

Если плоскости параллельны, то их нормальные векторы \(\boldsymbol\) и \(\boldsymbol_<1>\) коллинеарны, и существует такое число \(\lambda\), что \(\boldsymbol_ <1>= \lambda\boldsymbol\). В силу уравнений \eqref \(A_ <1>= (\boldsymbol_<1>, \boldsymbol_<1>) = \lambda(\boldsymbol_<1>, \boldsymbol) = \lambda A\). Аналогично доказываются и остальные равенства \eqref. Обратно, если равенства \eqref выполнены, то из формулы \eqref следует, что \(\boldsymbol_ <1>= \lambda\boldsymbol\). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия \eqref выражают не что иное, как коллинеарность векторов с компонентами \((A, B)\) и \((A_<1>, B_<1>)\). Точно так же условия \eqref означают коллинеарность векторов с компонентами \((A, B, C)\) и \((A_<1>, B_<1>, C_<1>)\). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
\begin
A& B\\
A_<1>& B_<1>
\end
= 0,\label
$$
а условие параллельности плоскостей — в виде
$$
\begin
B& C\\
B_<1>& C_<1>
\end =
\begin
C& A\\
C_<1>& A_<1>
\end =
\begin
A& B\\
A_<1>& B_<1>
\end
= 0.\label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии \eqref система линейных уравнений
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от \(C\) и \(C_<1>\). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
\begin
A& B\\
A_<1>& B_<1>
\end
\neq 0.\nonumber
$$
то при любых \(C\) и \(C_<1>\) система имеет единственное решение \((x, y)\).

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
\left\<\begin
Ax+By+Cz+D = 0,\\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
\end\right.\label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно \eqref означает, что хоть один из детерминантов отличен от нуля:
$$
\begin
B& C\\
B_<1>& C_<1>
\end^ <2>+
\begin
C& A\\
C_<1>& A_<1>
\end^ <2>+
\begin
A& B\\
A_<1>& B_<1>
\end^<2>
\neq 0.\label
$$

Разумеется, систему \eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой \eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = \frac><\alpha_<1>>,\ t = \frac><\alpha_<2>>,\ t = \frac><\alpha_<3>>,\nonumber
$$
и мы получаем два равенства
$$
\frac><\alpha_<2>> = \frac><\alpha_<3>>,\ \frac><\alpha_<1>> = \frac><\alpha_<3>>,\label
$$
или, в более симметричном виде,
$$
\frac><\alpha_<1>> = \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Уравнения \eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная \(x\)), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, \(\alpha_<1>\), то уравнения прямой принимают вид
$$
x = x_<0>,\ \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Эта прямая лежит в плоскости \(x = x_<0>\) и, следовательно, параллельна плоскости \(x = 0\). Аналогично пишутся уравнения прямой, если в нуль обращается не \(\alpha_<1>\), а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, \(\alpha_<1>\) и \(\alpha_<2>\), то прямая имеет уравнения
$$
x = x_<0>,\ y = y_<0>.\label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений \eqref. По условию \eqref один из детерминантов отличен от нуля. Допустим для определенности, что \(AB_<1>-A_<1>B \neq 0\). В силу утверждения 9 при любом фиксированном \(z\) система уравнений будет иметь единственное решение \((x, y)\), в котором \(x\) и \(y\), разумеется, зависят от \(z\). Они — линейные многочлены от \(z\): \(x = \alpha_<1>z+\beta_<1>\), \(y = \alpha_<2>z+\beta_<2>\).

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя \(z\) на \(t\), получаем параметрические уравнения прямой
$$
x = \alpha_<1>t+\beta_<1>,\ y = \alpha_<2>t+\beta_<2>,\ z = t.\nonumber
$$

Первые две координаты начальной точки прямой \(M_<0>(\beta_<1>, \beta_<2>, 0)\) можно получить, решая систему \eqref при значении \(z = 0\).

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты \((\alpha_<1>, \alpha_<2>, 1)\). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами \((A, B, C)\) и \(A_<1>, B_<1>, C_<1>\) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой \eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
\begin
B& C\\
B_<1>& C_<1>
\end,\
\begin
C& A\\
C_<1>& A_<1>
\end,\
\begin
A& B\\
A_<1>& B_<1>
\end.\label
$$

Вектор с компонентами \eqref есть направляющий вектор прямой с уравнениями \eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого \((\alpha_<1>, \alpha_<2>, \alpha_<3>)\) удовлетворяют уравнению \(A\alpha_<1>+B\alpha_<2>+C\alpha_ <3>= 0\), параллелен плоскости с уравнением \(Ax+By+Cz+D = 0\). Если, кроме того, он удовлетворяет уравнению \(A_<1>\alpha_<1>+B_<1>\alpha_<2>+C_<1>\alpha_ <3>= 0\), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами \eqref ненулевой в силу неравенства \eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

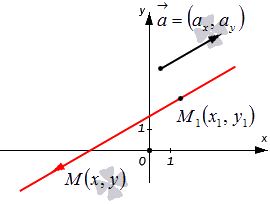
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

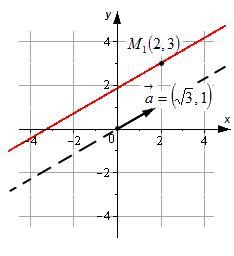
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .

Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3

Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :

x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2

Решение

Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ

Ответ: x = 3 · λ y = — 1 3 + 4 · λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .

Решение

Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:

4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:

— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

1. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ

Ответ: x = 1 2 + x · λ y = 2 3 — λ .

Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ

Ответ: x = 3 · λ y = — 7 — 2 · λ

1. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .

Уравнения плоскости, компланарной двум неколлинеарным векторам

Напомним, что три или более векторов называются компланарными , если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам .

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим — радиус-векторы точек и (рис.4.16).

Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

Параметрическое уравнение плоскости

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и компланарны (см. разд. 1.3.2). Запишем условие компланарности: где — некоторые действительные числа (параметры). Учитывая, что получим векторное параметрическое уравнение плоскости :

где — направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

где и — координаты направляющих векторов и соответственно. Параметры в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины пропорциональны расстоянию от заданной точки до точки принадлежащей плоскости. При точка совпадает с заданной точкой . При возрастании (или ) точка перемещается в направлении вектора (или ), а при убывании (или ) — в противоположном направлении.

1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.

2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору для этой плоскости. Поэтому их скалярное произведение равно нулю:

Следовательно, координаты и направляющих векторов и плоскости и ее нормали связаны однородными уравнениями:

3. Направляющие векторы плоскости определяются неоднозначно.

4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:

1) найти любое решение уравнения определяя тем самым координаты точки принадлежащей плоскости;

2) найти любые два линейно независимых решения однородного уравнения определяя тем самым координаты решения и направляющих векторов и плоскости;

3) записать параметрическое уравнение (4.20).

5. Чтобы перейти от параметрического уравнения плоскости к общему , достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:

и записать общее уравнение плоскости в форме (4.14):

6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.

Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки и (см. рис.4.11). Требуется:

а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам и

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:

1) находим любое решение уравнения , например, следовательно, точка принадлежит плоскости;

2) находим два линейно независимых (непропорциональных) решения однородного уравнения например и следовательно, векторы являются направляющими для плоскости;

3) записываем параметрическое уравнение плоскости (4.20):

б) Координаты середины отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов и

Составляем уравнение (4.14):

Тот же результат можно получить, записывая уравнение (4.18):